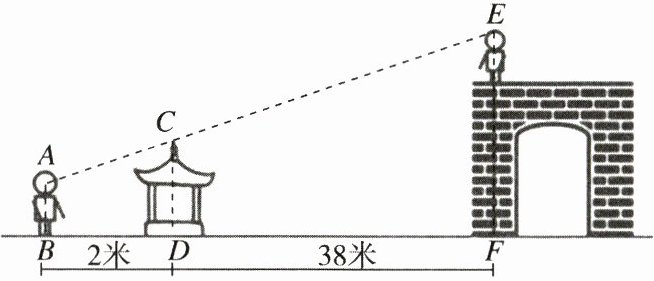
19. (8分)某天小明和小亮去某影视基地游玩,当小明给站在城楼上的小亮照相时发现他自己的眼睛、凉亭
顶端、小亮头顶三点恰好在一条直线上(如图).已知小明的眼睛离地面1.6米,凉亭顶端离地面1.9米,
小明到凉亭的距离为2米,凉亭离城楼底部的距离为38米,小亮身高为1.7米.请根据以上数据求出城
楼的高度.
顶端、小亮头顶三点恰好在一条直线上(如图).已知小明的眼睛离地面1.6米,凉亭顶端离地面1.9米,
小明到凉亭的距离为2米,凉亭离城楼底部的距离为38米,小亮身高为1.7米.请根据以上数据求出城
楼的高度.

答案:
解:如图,过点A作AM⊥EF于点M,交CD于点N. 由题意得,AN=2米,CN=1.9 - 1.6 = 0.3(米),MN=38米.
由题意得,AN=2米,CN=1.9 - 1.6 = 0.3(米),MN=38米.
∵CN//EM,
∴△ACN∽△AEM,
∴$\frac{CN}{EM}=\frac{AN}{AM}$,
∴$\frac{0.3}{EM}=\frac{2}{40}$,
∴EM=6(米).
∵AB=MF=1.6米,
∴城楼的高度为6 + 1.6 - 1.7 = 5.9(米).
解:如图,过点A作AM⊥EF于点M,交CD于点N.
 由题意得,AN=2米,CN=1.9 - 1.6 = 0.3(米),MN=38米.
由题意得,AN=2米,CN=1.9 - 1.6 = 0.3(米),MN=38米.∵CN//EM,
∴△ACN∽△AEM,
∴$\frac{CN}{EM}=\frac{AN}{AM}$,
∴$\frac{0.3}{EM}=\frac{2}{40}$,
∴EM=6(米).
∵AB=MF=1.6米,
∴城楼的高度为6 + 1.6 - 1.7 = 5.9(米).
20. (8分)如图,在边长为1的5×5的正方形网格上有两个三角形,它们的顶点都在格点上.
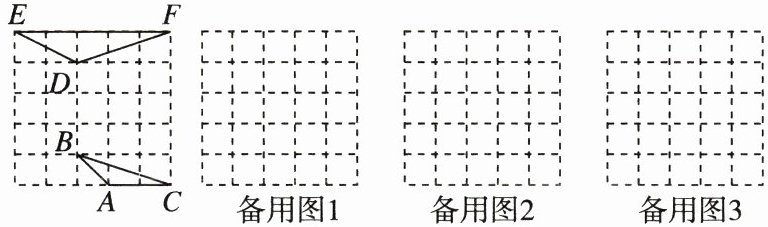
(1)△ABC与△DEF是否相似?请说明理由.
(2)还能在网格上画出与△ABC相似的三角形吗?还能画出几种大小不同的三角形?试着在备用图上
画出来.(三个顶点都在格点上)

(1)△ABC与△DEF是否相似?请说明理由.
(2)还能在网格上画出与△ABC相似的三角形吗?还能画出几种大小不同的三角形?试着在备用图上
画出来.(三个顶点都在格点上)
答案:
解:
(1)△ABC∽△DEF.理由如下:
∵$DE=\sqrt{2^2 + 1^2}=\sqrt{5}$,$DF=\sqrt{3^2 + 1^2}=\sqrt{10}$,EF=5,$AB=\sqrt{2}$,AC=2,$CB=\sqrt{1^2 + 3^2}=\sqrt{10}$,
∴$\frac{DE}{AB}=\frac{\sqrt{5}}{\sqrt{2}}=\frac{\sqrt{10}}{2}$,$\frac{DF}{AC}=\frac{\sqrt{10}}{2}$,$\frac{EF}{CB}=\frac{5}{\sqrt{10}}=\frac{\sqrt{10}}{2}$,
∴$\frac{DE}{AB}=\frac{DF}{AC}=\frac{EF}{CB}=\frac{\sqrt{10}}{2}$,
∴△ABC∽△DEF.
(2)还能画出三种大小不同的三角形,如图所示.
解:
(1)△ABC∽△DEF.理由如下:
∵$DE=\sqrt{2^2 + 1^2}=\sqrt{5}$,$DF=\sqrt{3^2 + 1^2}=\sqrt{10}$,EF=5,$AB=\sqrt{2}$,AC=2,$CB=\sqrt{1^2 + 3^2}=\sqrt{10}$,
∴$\frac{DE}{AB}=\frac{\sqrt{5}}{\sqrt{2}}=\frac{\sqrt{10}}{2}$,$\frac{DF}{AC}=\frac{\sqrt{10}}{2}$,$\frac{EF}{CB}=\frac{5}{\sqrt{10}}=\frac{\sqrt{10}}{2}$,
∴$\frac{DE}{AB}=\frac{DF}{AC}=\frac{EF}{CB}=\frac{\sqrt{10}}{2}$,
∴△ABC∽△DEF.
(2)还能画出三种大小不同的三角形,如图所示.

21. (8分)如图,四边形ABCD中,∠BAD= ∠B= 90°,∠C= 75°,AD= 2AB.

(1)尺规作图:在BC上求作一点E,使得∠AEC= 150°.(保留作图痕迹,不写作法)
(2)在(1)的条件下,连结DE.求证:△ADE∽△DCE.

(1)尺规作图:在BC上求作一点E,使得∠AEC= 150°.(保留作图痕迹,不写作法)
(2)在(1)的条件下,连结DE.求证:△ADE∽△DCE.
答案:
解:
(1)如图1,点E即为所求的点.
∵AD=AE,AD=2AB,
∴AE=2AB.
∵∠B=90°,
∴∠AEB=30°,
∴∠AEC=150°.
(2)证明:连结DE,如图2.
∵∠BAD=∠B=90°,
∴AD//BC,
∴∠DAE=∠AEB=30°.由作图得,AD=AE,
∴$∠ADE=∠AED=\frac{1}{2}(180° - ∠DAE)=75°$.
∵AD//BC,
∴∠DEC=∠ADE=75°.又
∵∠C=75°,
∴∠ADE=∠DCE,∠AED=∠DEC,
∴△ADE∽△DCE.
解:
(1)如图1,点E即为所求的点.
∵AD=AE,AD=2AB,

∴AE=2AB.
∵∠B=90°,
∴∠AEB=30°,
∴∠AEC=150°.
(2)证明:连结DE,如图2.
∵∠BAD=∠B=90°,

∴AD//BC,
∴∠DAE=∠AEB=30°.由作图得,AD=AE,
∴$∠ADE=∠AED=\frac{1}{2}(180° - ∠DAE)=75°$.
∵AD//BC,
∴∠DEC=∠ADE=75°.又
∵∠C=75°,
∴∠ADE=∠DCE,∠AED=∠DEC,
∴△ADE∽△DCE.
22. (10分)如图所示,已知△ABC的三边分别为a,b,c.
(1)如果∠A= 2∠B,求证$:a^2-b^2= bc.$
(2)如果$a^2-b^2= bc,$求证:∠A= 2∠B.
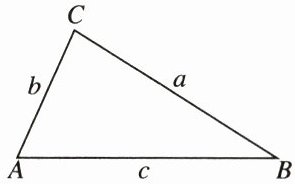
(1)如果∠A= 2∠B,求证$:a^2-b^2= bc.$
(2)如果$a^2-b^2= bc,$求证:∠A= 2∠B.

答案:
证明:
(1)如图1,延长CA到点E,使AE=AB=c,连结BE,则∠E=∠ABE,
∴∠BAC=∠E + ∠ABE=2∠E.
∵∠BAC=2∠ABC,
∴2∠ABC=2∠E,
∴∠ABC=∠E.
∵∠C=∠C,
∴△CAB∽△CBE,
∴$\frac{AC}{BC}=\frac{BC}{EC}$.
∵AC=b,BC=a,
∴$\frac{b}{a}=\frac{a}{b + c}$,
∴$a^2 - b^2=bc$.
(2)如图2,延长CA到点F,使AF=AB=c,连结BF,则∠F=∠ABF.
∵$a^2 - b^2=bc$,
∴$a^2=b^2 + bc=b(b + c)$,
∴$\frac{b}{a}=\frac{a}{b + c}$,
∴$\frac{AC}{BC}=\frac{BC}{FC}$.
∵∠C=∠C,
∴△ABC∽△BFC,
∴∠ABC=∠F,
∴∠BAC=∠ABF + ∠F=2∠ABC.

证明:
(1)如图1,延长CA到点E,使AE=AB=c,连结BE,则∠E=∠ABE,
∴∠BAC=∠E + ∠ABE=2∠E.
∵∠BAC=2∠ABC,
∴2∠ABC=2∠E,
∴∠ABC=∠E.
∵∠C=∠C,
∴△CAB∽△CBE,
∴$\frac{AC}{BC}=\frac{BC}{EC}$.
∵AC=b,BC=a,
∴$\frac{b}{a}=\frac{a}{b + c}$,
∴$a^2 - b^2=bc$.
(2)如图2,延长CA到点F,使AF=AB=c,连结BF,则∠F=∠ABF.
∵$a^2 - b^2=bc$,
∴$a^2=b^2 + bc=b(b + c)$,
∴$\frac{b}{a}=\frac{a}{b + c}$,
∴$\frac{AC}{BC}=\frac{BC}{FC}$.
∵∠C=∠C,
∴△ABC∽△BFC,
∴∠ABC=∠F,
∴∠BAC=∠ABF + ∠F=2∠ABC.


查看更多完整答案,请扫码查看


