22. (10分)如图,AB为⊙O的直径,AC是⊙O的一条弦,D为$\widehat{BC}$的中点,作DE⊥AC于点E,ED的延长线交AB的延长线于点F,连结DA。
(1)若AB= 90,求圆心O到EF的距离。
(2)若DA= DF= 6$\sqrt{3}$,求阴影部分的面积。(结果保留π)
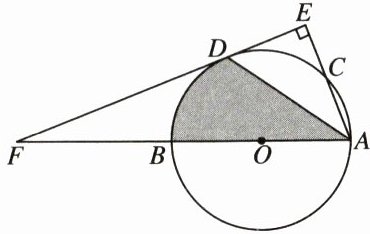
(1)若AB= 90,求圆心O到EF的距离。
(2)若DA= DF= 6$\sqrt{3}$,求阴影部分的面积。(结果保留π)

答案:
解:
(1)如图,连结OD.

∵D为$\overset{\frown}{BC}$的中点,
∴∠CAD=∠BAD.
∵OA=OD,
∴∠BAD=∠ADO,
∴∠CAD=∠ADO,
∴OD//AE.
∵DE⊥AC,
∴OD⊥EF,
∴OD的长度是圆心O到EF的距离.
∵AB=90,
∴OD= $\frac{1}{2}AB=45$.
(2)如图,过点O作OG⊥AD交AD于点G.
∵DA=DF,
∴∠F=∠BAD.
由
(1)得∠CAD=∠BAD,
∴∠F=∠CAD.
∵∠F+∠BAD+∠CAD=90°,
∴∠F=∠BAD=∠CAD=30°,
∴∠BOD=2∠BAD=60°,OF=2OD.
∵在Rt△ODF中,$OF^2 - OD^2=DF^2$,
∴$(2OD)^2 - OD^2=(6\sqrt{3})^2$,解得OD=6.
在Rt△OAG中,OA=OD=6,∠OAG=30°,OG= $\frac{1}{2}×6 = 3$,
∴$S_{\triangle AOD}=\frac{1}{2}×6\sqrt{3}×3=9\sqrt{3}$,
∴$S_{阴影}=S_{扇形BOD}+S_{\triangle AOD}=\frac{60\pi×6^2}{360}+9\sqrt{3}=6\pi+9\sqrt{3}$.
解:
(1)如图,连结OD.

∵D为$\overset{\frown}{BC}$的中点,
∴∠CAD=∠BAD.
∵OA=OD,
∴∠BAD=∠ADO,
∴∠CAD=∠ADO,
∴OD//AE.
∵DE⊥AC,
∴OD⊥EF,
∴OD的长度是圆心O到EF的距离.
∵AB=90,
∴OD= $\frac{1}{2}AB=45$.
(2)如图,过点O作OG⊥AD交AD于点G.
∵DA=DF,
∴∠F=∠BAD.
由
(1)得∠CAD=∠BAD,
∴∠F=∠CAD.
∵∠F+∠BAD+∠CAD=90°,
∴∠F=∠BAD=∠CAD=30°,
∴∠BOD=2∠BAD=60°,OF=2OD.
∵在Rt△ODF中,$OF^2 - OD^2=DF^2$,
∴$(2OD)^2 - OD^2=(6\sqrt{3})^2$,解得OD=6.
在Rt△OAG中,OA=OD=6,∠OAG=30°,OG= $\frac{1}{2}×6 = 3$,
∴$S_{\triangle AOD}=\frac{1}{2}×6\sqrt{3}×3=9\sqrt{3}$,
∴$S_{阴影}=S_{扇形BOD}+S_{\triangle AOD}=\frac{60\pi×6^2}{360}+9\sqrt{3}=6\pi+9\sqrt{3}$.
23. (10分)如图,A,P,B,C在圆上,∠APC= ∠CPB= 60°,连结AB,BC,AC。
(1)判断△ABC的形状,并证明你的结论。
(2)若∠PAC= 90°,AB= 2$\sqrt{3}$,求圆的半径。
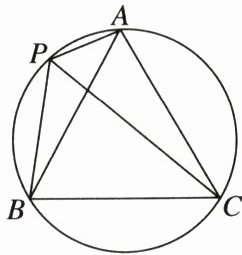
(1)判断△ABC的形状,并证明你的结论。
(2)若∠PAC= 90°,AB= 2$\sqrt{3}$,求圆的半径。

答案:
解:
(1)△ABC是等边三角形.
证明:
∵∠APC=60°,$\overset{\frown}{AC}=\overset{\frown}{AC}$,
∴∠ABC=∠APC=60°,
同理,∠BAC=∠CPB=60°,
∴∠ABC=∠BAC=∠ACB=60°,
∴△ABC是等边三角形.
(2)由
(1)得AC=AB=2$\sqrt{3}$,
∵∠PAC=90°,
∴线段PC为圆的直径.
在Rt△PAC中,∠APC=60°,AC=2$\sqrt{3}$,
∴AP=2,PC=4,
∴圆的半径是2.
(1)△ABC是等边三角形.
证明:
∵∠APC=60°,$\overset{\frown}{AC}=\overset{\frown}{AC}$,
∴∠ABC=∠APC=60°,
同理,∠BAC=∠CPB=60°,
∴∠ABC=∠BAC=∠ACB=60°,
∴△ABC是等边三角形.
(2)由
(1)得AC=AB=2$\sqrt{3}$,
∵∠PAC=90°,
∴线段PC为圆的直径.
在Rt△PAC中,∠APC=60°,AC=2$\sqrt{3}$,
∴AP=2,PC=4,
∴圆的半径是2.
24. (12分)如图,在△ABC中,D在边AC上,圆O为锐角三角形BCD的外接圆,连结CO并延长交AB于点E。
(1)如图1,若∠DBC= α,请用含α的代数式表示∠DCE。
(2)如图2,作BF⊥AC,垂足为点F,BF与CE交于点G,已知∠ABD= ∠CBF。
①求证:EB= EG。
②若CE= 5,AC= 8,求FG+FB的值。
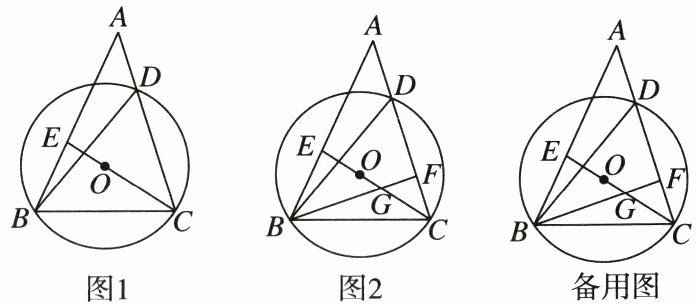
(1)如图1,若∠DBC= α,请用含α的代数式表示∠DCE。
(2)如图2,作BF⊥AC,垂足为点F,BF与CE交于点G,已知∠ABD= ∠CBF。
①求证:EB= EG。
②若CE= 5,AC= 8,求FG+FB的值。

答案:
解:
(1)如图1,连结OD.
∵∠DOC=2∠DBC=2α,又
∵OD=OC,
∴∠DCE=90° - α.

(2)①证明:
∵∠ABD=∠CBF,
∴∠EBG=∠ABD+∠DBF=∠CBF+∠DBF=∠DBC.设∠DBC=α,由
(1)得∠DCE=90° - α.
∵BF⊥AC,
∴∠FGC=∠BGE=α,
∴∠EBG=∠EGB,
∴EB=EG.
②如图2,作EM⊥BF,EN⊥AC.由①得∠EBG=α,∠ACE=90° - α,
∵BF⊥AC,

∴∠A=90° - α,
∴AE=CE=5.
∵EN⊥AC,AC=8,
∴CN=4,
∴EN=3.
∵EM⊥BF,NF⊥BF,EN⊥AC,
∴四边形EMFN为矩形,
∴EN=MF=3.
∵EB=EG,EM⊥BG,
∴BM=GM,
∴FG+FB=FM - MG+FM+BM=2FM=6.
解:
(1)如图1,连结OD.
∵∠DOC=2∠DBC=2α,又
∵OD=OC,
∴∠DCE=90° - α.

(2)①证明:
∵∠ABD=∠CBF,
∴∠EBG=∠ABD+∠DBF=∠CBF+∠DBF=∠DBC.设∠DBC=α,由
(1)得∠DCE=90° - α.
∵BF⊥AC,
∴∠FGC=∠BGE=α,
∴∠EBG=∠EGB,
∴EB=EG.
②如图2,作EM⊥BF,EN⊥AC.由①得∠EBG=α,∠ACE=90° - α,
∵BF⊥AC,

∴∠A=90° - α,
∴AE=CE=5.
∵EN⊥AC,AC=8,
∴CN=4,
∴EN=3.
∵EM⊥BF,NF⊥BF,EN⊥AC,
∴四边形EMFN为矩形,
∴EN=MF=3.
∵EB=EG,EM⊥BG,
∴BM=GM,
∴FG+FB=FM - MG+FM+BM=2FM=6.
查看更多完整答案,请扫码查看


