10. 已知二次函数$y= x^2+ax+b= (x-x_1)(x-x_2)(a,b,x_1,x_2$为常数),若$1<x_1<x_2<3$,记$t= a+b$,则 ( )
A.$-3<t<0$
B.$-1<t<0$
C.$-1<t<3$
D.$0<t<3$
A.$-3<t<0$
B.$-1<t<0$
C.$-1<t<3$
D.$0<t<3$
答案:
C [解析]
∵y=x²+ax+b=(x-x₁)(x-x₂),二次项系数1>0,
∴抛物线开口向上,与x轴的交点坐标为(x₁,0),(x₂,0),1<x₁<x₂<3,
∴当x=1时,y=1+a+b>0,即1+t>0,
∴t>-1.
又对称轴方程为x=-$\frac{a}{2}$,
此时y=b-$\frac{a²}{4}$<0,
∴b<$\frac{a²}{4}$,
∴a+b<a+$\frac{a²}{4}$=$\frac{1}{4}$(a+2)²-1.
∵1<-$\frac{a}{2}$<3,
∴-6<a<-2,
∴-1<$\frac{1}{4}$(a+2)²-1<3.
综上所述,t的取值范围是-1<t<3.
∵y=x²+ax+b=(x-x₁)(x-x₂),二次项系数1>0,
∴抛物线开口向上,与x轴的交点坐标为(x₁,0),(x₂,0),1<x₁<x₂<3,
∴当x=1时,y=1+a+b>0,即1+t>0,
∴t>-1.
又对称轴方程为x=-$\frac{a}{2}$,
此时y=b-$\frac{a²}{4}$<0,
∴b<$\frac{a²}{4}$,
∴a+b<a+$\frac{a²}{4}$=$\frac{1}{4}$(a+2)²-1.
∵1<-$\frac{a}{2}$<3,
∴-6<a<-2,
∴-1<$\frac{1}{4}$(a+2)²-1<3.
综上所述,t的取值范围是-1<t<3.
11. 已知线段$a= 4\,cm,b= 9\,cm$,则线段$a,b$的比例中项为______$cm$.
答案:
6
12. 已知$(-3,y_1),(4,y_2)是二次函数y= x^2-4x$上的点,则$y_1,y_2$的大小关系为______(用“<”连接).
答案:
y₂<y₁
13. 在一个不透明盒子里,装有若干个红色、白色的小球(除了颜色外均相同),将球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复. 下表是一组统计数据:
| 摸球的次数$n$ | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到红球的次数$m$ | 59 | 96 | 116 | 295 | 480 | 601 |
| 摸到红球的频率$\frac{m}{n}$ | 0.59 | 0.64 | 0.58 | 0.59 | 0.60 | 0.601 |

根据上表估计“摸到红球”的概率是______.(精确到0.1)
| 摸球的次数$n$ | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到红球的次数$m$ | 59 | 96 | 116 | 295 | 480 | 601 |
| 摸到红球的频率$\frac{m}{n}$ | 0.59 | 0.64 | 0.58 | 0.59 | 0.60 | 0.601 |

根据上表估计“摸到红球”的概率是______.(精确到0.1)
答案:
0.6
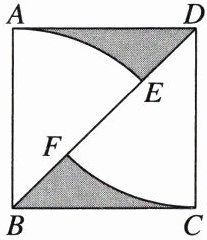
14. 如图,正方形$ABCD$的边长为2,连结$BD$,分别以$B,D$为圆心,以$AB$长为半径画弧,交$BD于E,F$两点,则图中阴影部分的面积为______.
]
]
答案:
4-π
15. 已知$0<m<3$,若二次函数$y= ax^2+bx+c(a,b,c$是常数,$a\neq0)的自变量x与函数值y$的部分对应值如下表,则$c= $______,方程$ax^2+bx+c= 0$的两根为______.



答案:
3 x₁=-7,x₂=5
16. 定义:有一组邻边相等且对角互补的四边形叫做等补四边形.
例:如图1,四边形$ABCD内接于\odot O$,$AB= AD$. 则四边形$ABCD$是等补四边形.
探究与运用:如图2,在等补四边形$ABCD$中,$AB= AD$,其外角$\angle EAD的平分线交CD的延长线于点F$. 若$CD= 10,AF= 5$,则$DF$的长为______.
]

例:如图1,四边形$ABCD内接于\odot O$,$AB= AD$. 则四边形$ABCD$是等补四边形.
探究与运用:如图2,在等补四边形$ABCD$中,$AB= AD$,其外角$\angle EAD的平分线交CD的延长线于点F$. 若$CD= 10,AF= 5$,则$DF$的长为______.
]

答案:
5$\sqrt{2}$-5 [解析]如图,连结AC.
∵四边形ABCD是等补四边形,
∴∠BAD+∠BCD=180°.

又∠BAD+∠EAD=180°,
∴∠EAD=∠BCD.
∵AF平分∠EAD,
∴∠FAD=$\frac{1}{2}$∠EAD.
∵四边形ABCD是等补四边形,
∴A,B,C,D四点共圆.
∵AB=AD,
∴$\overset{\frown}{AB}$=$\overset{\frown}{AD}$,
∴∠ACD=∠ACB,
∴∠FCA=$\frac{1}{2}$∠BCD,
∴∠FCA=∠FAD.又∠AFC=∠DFA,
∴△ACF∽△DAF,
∴$\frac{AF}{DF}$=$\frac{CF}{AF}$,即$\frac{5}{DF}$=$\frac{DF+10}{5}$,
∴DF=5$\sqrt{2}$-5.
5$\sqrt{2}$-5 [解析]如图,连结AC.
∵四边形ABCD是等补四边形,
∴∠BAD+∠BCD=180°.

又∠BAD+∠EAD=180°,
∴∠EAD=∠BCD.
∵AF平分∠EAD,
∴∠FAD=$\frac{1}{2}$∠EAD.
∵四边形ABCD是等补四边形,
∴A,B,C,D四点共圆.
∵AB=AD,
∴$\overset{\frown}{AB}$=$\overset{\frown}{AD}$,
∴∠ACD=∠ACB,
∴∠FCA=$\frac{1}{2}$∠BCD,
∴∠FCA=∠FAD.又∠AFC=∠DFA,
∴△ACF∽△DAF,
∴$\frac{AF}{DF}$=$\frac{CF}{AF}$,即$\frac{5}{DF}$=$\frac{DF+10}{5}$,
∴DF=5$\sqrt{2}$-5.
17. (8分)已知二次函数$y= 2x^2+bx+1的图象过点(2,3)$,若点$P(m,m^2+1)$也在该二次函数的图象上,求点$P$的坐标.
答案:
解:
∵二次函数y=2x²+bx+1的图象过点(2,3),
∴3=8+2b+1,
∴b=-3,
∴该二次函数的表达式为y=2x²-3x+1.
∵点P(m,m²+1)也在该二次函数的图象上,
∴m²+1=2m²-3m+1,
解得m₁=0,m₂=3,
∴点P的坐标为(0,1)或(3,10).
∵二次函数y=2x²+bx+1的图象过点(2,3),
∴3=8+2b+1,
∴b=-3,
∴该二次函数的表达式为y=2x²-3x+1.
∵点P(m,m²+1)也在该二次函数的图象上,
∴m²+1=2m²-3m+1,
解得m₁=0,m₂=3,
∴点P的坐标为(0,1)或(3,10).
查看更多完整答案,请扫码查看


