22. (10分)在学习了光的反射定律后,数学综合实践小组想利用光的反射定律(反射角等于入射角)测量池塘对岸一棵树的高度$AB$,测量步骤如下:
①如图,在地面上的点$E$处放置一块平面镜(镜子大小忽略不计),小阳站在$BE$的延长线上,当小阳从平面镜中刚好看到树的顶点$A$时,测得小阳到平面镜的距离$DE= 2\ m$,小阳的眼睛点$C到地面的距离CD= 1.6\ m$;
②将平面镜从点$E沿BE的延长线移动6\ m放置到点H$处,小阳从点$D处移动到点G$,此时小阳的眼睛点$F又刚好在平面镜中看到树的顶点A$,这时测得小阳到平面镜的距离$GH= 3.2\ m$.
请根据以上测量过程及数据求出树的高度$AB$.

①如图,在地面上的点$E$处放置一块平面镜(镜子大小忽略不计),小阳站在$BE$的延长线上,当小阳从平面镜中刚好看到树的顶点$A$时,测得小阳到平面镜的距离$DE= 2\ m$,小阳的眼睛点$C到地面的距离CD= 1.6\ m$;
②将平面镜从点$E沿BE的延长线移动6\ m放置到点H$处,小阳从点$D处移动到点G$,此时小阳的眼睛点$F又刚好在平面镜中看到树的顶点A$,这时测得小阳到平面镜的距离$GH= 3.2\ m$.
请根据以上测量过程及数据求出树的高度$AB$.

答案:
解:由题意可知,∠CED=∠AEB,∠CDE=∠ABE,∠AHB=∠FHG,∠FGH=∠ABH,
∴△CDE∽△ABE,△FGH∽△ABH,
∴$\frac{CD}{AB}$=$\frac{DE}{BE}$,$\frac{FG}{AB}$=$\frac{GH}{BH}$,
∴$\frac{1.6}{AB}$=$\frac{2}{BE}$,$\frac{1.6}{AB}$=$\frac{3.2}{BE+HE}$=$\frac{3.2}{BE+6}$,
∴$\frac{2}{BE}$=$\frac{3.2}{BE+6}$,解得BE=10m,
∴AB=8m.答:树的高度AB为8m.
∴△CDE∽△ABE,△FGH∽△ABH,
∴$\frac{CD}{AB}$=$\frac{DE}{BE}$,$\frac{FG}{AB}$=$\frac{GH}{BH}$,
∴$\frac{1.6}{AB}$=$\frac{2}{BE}$,$\frac{1.6}{AB}$=$\frac{3.2}{BE+HE}$=$\frac{3.2}{BE+6}$,
∴$\frac{2}{BE}$=$\frac{3.2}{BE+6}$,解得BE=10m,
∴AB=8m.答:树的高度AB为8m.
23. (10分)在平面直角坐标系$xOy$中,$M(x_1,y_1),N(x_2,y_2)是抛物线y= ax^2+bx+c$上任意两点.设抛物线的对称轴是直线$x= t$.
(1)若对于$x_1= 2,x_2= -1$,有$y_1= y_2$,求$t$的值.
(2)当$a<0$时,若对于$x_1\geq2$,都有$y_1<c$成立,并且对于$x_2>1$,存在$y_2>c$,求$t$的取值范围.
(1)若对于$x_1= 2,x_2= -1$,有$y_1= y_2$,求$t$的值.
(2)当$a<0$时,若对于$x_1\geq2$,都有$y_1<c$成立,并且对于$x_2>1$,存在$y_2>c$,求$t$的取值范围.
答案:
(1)t=$\frac{2−1}{2}$=$\frac{1}{2}$.
(2)由题意可知,抛物线y=ax²+bx+c与y轴的交点为(0,c),当a<0时,抛物线开口向下,且经过(0,c),(2t,c),若抛物线经过点(1,c),则t=$\frac{1}{2}$,若抛物线经过点(2,c),则t=1,①当t≤$\frac{1}{2}$时,t≤0<1或0<t≤2t≤1,
∴对于x₂>1,都有y<c,与“对于x₂>1,存在y₂>c”不符,
∴不合题意.②当$\frac{1}{2}$<t<1时,t<1<2t<2,
∴对于x₂>1,存在y>c;对于x₁≥2,都有y₁<c,
∴$\frac{1}{2}$<t<1成立.③当t≥1时,0<2≤2t,
∴当x₁=2时,有y₁≥c,与“对于x₁≥2,都有y₁<c"不符,
∴不合题意.综上所述,$\frac{1}{2}$<t<1.
(1)t=$\frac{2−1}{2}$=$\frac{1}{2}$.
(2)由题意可知,抛物线y=ax²+bx+c与y轴的交点为(0,c),当a<0时,抛物线开口向下,且经过(0,c),(2t,c),若抛物线经过点(1,c),则t=$\frac{1}{2}$,若抛物线经过点(2,c),则t=1,①当t≤$\frac{1}{2}$时,t≤0<1或0<t≤2t≤1,
∴对于x₂>1,都有y<c,与“对于x₂>1,存在y₂>c”不符,
∴不合题意.②当$\frac{1}{2}$<t<1时,t<1<2t<2,
∴对于x₂>1,存在y>c;对于x₁≥2,都有y₁<c,
∴$\frac{1}{2}$<t<1成立.③当t≥1时,0<2≤2t,
∴当x₁=2时,有y₁≥c,与“对于x₁≥2,都有y₁<c"不符,
∴不合题意.综上所述,$\frac{1}{2}$<t<1.
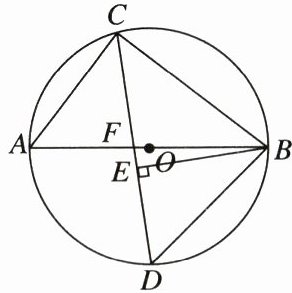
24. (12分)如图,$\triangle ABC是\odot O$的内接三角形,$AB是\odot O$的直径,$AC= 3,BC= 4,CD平分\angle ACB$,交$AB于点F$,连结$BD$,作$BE\perp CD$,垂足为$E$.
(1)求证:$\triangle ACF\backsim\triangle DCB$.
(2)求证:$AC+BC= \sqrt{2}CD$.
(3)求$CF$的长.
(1)求证:$\triangle ACF\backsim\triangle DCB$.
(2)求证:$AC+BC= \sqrt{2}CD$.
(3)求$CF$的长.

答案:
(1)证明:
∵CD平分∠ACB,
∴∠ACF=∠DCB.
∵∠CAF=∠CDB,
∴△ACF∽△DCB.
(2)证明:如图,连结AD,作AH⊥CD于点H,则∠AHC=∠AHD=90°.
∵BE⊥CD于点E,
∴∠BEC=∠DEB=90°,
∴∠AHD=∠DEB.
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
∴∠ACH=∠BCE=$\frac{1}{2}$∠ACB=45°,∠ADH=∠DBE=90°−∠BDE,
∴∠CAH=∠ACH=45°,∠CBE=∠BCE=45°,
∴AH=CH,BE=CE,
∴AC=$\sqrt{AH²+CH²}$=$\sqrt{2}$AH,BC=$\sqrt{BE²+CE²}$=$\sqrt{2}$CE.
∵∠AHD=∠DEB,∠ADH=∠DBE,
∴△AHD∽△DEB.
∵$\widehat{AD}=\widehat{DB}$,
∴AD=DB.
∵$\frac{AH}{DE}$=$\frac{AD}{DB}$=1,
∴AH=DE,
∴AC=$\sqrt{2}$DE,
∴AC+BC=$\sqrt{2}$DE+$\sqrt{2}$CE=$\sqrt{2}$CD.
(3)
∵AC=3,BC=4,且AC+BC=$\sqrt{2}$CD,
∴3+4=$\sqrt{2}$CD,
∴CD=$\frac{7\sqrt{2}}{2}$.
∵AB=$\sqrt{AD²+DB²}$=$\sqrt{2}$DB,且AB=$\sqrt{AC²+BC²}$=$\sqrt{3²+4²}$=5,
∴$\sqrt{2}$DB=5,
∴DB=$\frac{5\sqrt{2}}{2}$.
∵△ACF∽△DCB,
∴$\frac{CF}{CB}$=$\frac{AC}{CD}$,
∴CF=$\frac{AC\cdot CB}{CD}$=$\frac{3×4}{\frac{7\sqrt{2}}{2}}$=$\frac{12\sqrt{2}}{7}$,
∴CF的长是$\frac{12\sqrt{2}}{7}$.
(1)证明:
∵CD平分∠ACB,
∴∠ACF=∠DCB.
∵∠CAF=∠CDB,
∴△ACF∽△DCB.
(2)证明:如图,连结AD,作AH⊥CD于点H,则∠AHC=∠AHD=90°.
∵BE⊥CD于点E,
∴∠BEC=∠DEB=90°,
∴∠AHD=∠DEB.
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
∴∠ACH=∠BCE=$\frac{1}{2}$∠ACB=45°,∠ADH=∠DBE=90°−∠BDE,
∴∠CAH=∠ACH=45°,∠CBE=∠BCE=45°,
∴AH=CH,BE=CE,
∴AC=$\sqrt{AH²+CH²}$=$\sqrt{2}$AH,BC=$\sqrt{BE²+CE²}$=$\sqrt{2}$CE.
∵∠AHD=∠DEB,∠ADH=∠DBE,
∴△AHD∽△DEB.
∵$\widehat{AD}=\widehat{DB}$,
∴AD=DB.
∵$\frac{AH}{DE}$=$\frac{AD}{DB}$=1,
∴AH=DE,
∴AC=$\sqrt{2}$DE,
∴AC+BC=$\sqrt{2}$DE+$\sqrt{2}$CE=$\sqrt{2}$CD.
(3)
∵AC=3,BC=4,且AC+BC=$\sqrt{2}$CD,
∴3+4=$\sqrt{2}$CD,
∴CD=$\frac{7\sqrt{2}}{2}$.
∵AB=$\sqrt{AD²+DB²}$=$\sqrt{2}$DB,且AB=$\sqrt{AC²+BC²}$=$\sqrt{3²+4²}$=5,
∴$\sqrt{2}$DB=5,
∴DB=$\frac{5\sqrt{2}}{2}$.
∵△ACF∽△DCB,
∴$\frac{CF}{CB}$=$\frac{AC}{CD}$,
∴CF=$\frac{AC\cdot CB}{CD}$=$\frac{3×4}{\frac{7\sqrt{2}}{2}}$=$\frac{12\sqrt{2}}{7}$,
∴CF的长是$\frac{12\sqrt{2}}{7}$.
查看更多完整答案,请扫码查看


