19. (8分)如图,PA,PB分别与⊙O相切于点A,B,AC为弦,BC为⊙O的直径,若∠P= 60°,PB= 2 cm.
(1)求证:△PAB是等边三角形.
(2)求AC的长.
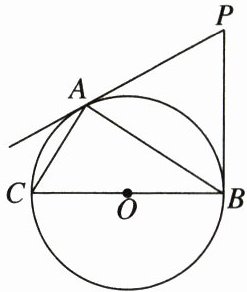
(1)求证:△PAB是等边三角形.
(2)求AC的长.

答案:
解:
(1)证明:
∵PA,PB分别与⊙O相切于点A,B,
∴PA=PB.又∠P=60°,
∴△PAB是等边三角形.
(2)
∵△PAB是等边三角形,
∴PB=AB=2 cm,∠PBA=60°.
∵BC是⊙O的直径,PB是⊙O的切线,
∴∠CAB=90°,∠PBC=90°,
∴∠ABC=30°,
∴tan∠ABC=AC/AB=√3/3,
∴AC=2×√3/3=2√3/3(cm).
(1)证明:
∵PA,PB分别与⊙O相切于点A,B,
∴PA=PB.又∠P=60°,
∴△PAB是等边三角形.
(2)
∵△PAB是等边三角形,
∴PB=AB=2 cm,∠PBA=60°.
∵BC是⊙O的直径,PB是⊙O的切线,
∴∠CAB=90°,∠PBC=90°,
∴∠ABC=30°,
∴tan∠ABC=AC/AB=√3/3,
∴AC=2×√3/3=2√3/3(cm).
20. (8分)如图,△ABC内接于⊙O,AB= AC,AD是⊙O的直径,交BC于点E,过点D作DF//BC,交AB的延长线于点F,连结BD.
(1)求证:DF是⊙O的切线.
(2)若AC= 4,AF= 6,求BD的长.

(1)求证:DF是⊙O的切线.
(2)若AC= 4,AF= 6,求BD的长.

答案:
解:
(1)证明:
∵AD是⊙O的直径,
∴∠ABD=90°,
即∠ABC+∠CBD=90°.
∵AB=AC,
∴∠ABC=∠C.
∵∠ADB=∠C,
∴∠ABC=∠ADB.
∵BC//DF,
∴∠CBD=∠FDB,
∴∠ADB+∠FDB=90°,
即∠ADF=90°,
∴AD⊥DF.
又
∵OD是⊙O的半径,
∴DF是⊙O的切线.
(2)
∵AB=AC=4,AF=6,
∴BF=AF - AB=2.
∵∠ADF=90°,∠ABD=90°,
∴∠BAD=∠BDF,
∴△BDF∽△BAD,
∴BD²=BF×AB=2×4=8,
∴BD=2√2.
(1)证明:
∵AD是⊙O的直径,
∴∠ABD=90°,
即∠ABC+∠CBD=90°.
∵AB=AC,
∴∠ABC=∠C.
∵∠ADB=∠C,
∴∠ABC=∠ADB.
∵BC//DF,
∴∠CBD=∠FDB,
∴∠ADB+∠FDB=90°,
即∠ADF=90°,
∴AD⊥DF.
又
∵OD是⊙O的半径,
∴DF是⊙O的切线.
(2)
∵AB=AC=4,AF=6,
∴BF=AF - AB=2.
∵∠ADF=90°,∠ABD=90°,
∴∠BAD=∠BDF,
∴△BDF∽△BAD,
∴BD²=BF×AB=2×4=8,
∴BD=2√2.
21. (8分)如图,在Rt△ABC中,∠C= 90°,AB= c,AC= b,BC= a,⊙O是△ABC的内切圆,求⊙O的半径r(用含a,b,c的代数式表示).

(1)小旭同学用面积法,可以构建关于r的方程______,解得r= ______.(结果用含a,b,c的代数式表示)
小辰同学由切线长定理,可以构建关于r的方程______,解得r= ______.(结果用含a,b,c的代数式表示)
(2)两名同学得到的答案相等吗?若相等,请给出证明.

(1)小旭同学用面积法,可以构建关于r的方程______,解得r= ______.(结果用含a,b,c的代数式表示)
小辰同学由切线长定理,可以构建关于r的方程______,解得r= ______.(结果用含a,b,c的代数式表示)
(2)两名同学得到的答案相等吗?若相等,请给出证明.
答案:
解:
(1)设D,E,F分别为切点.
方法一(面积法):如图,连结OA,OB,OC,OD,OE,OF,则OF⊥AB,OD⊥BC,OE⊥AC.
∵S△ABC=S△AOB+S△AOC+S△BOC,
∴1/2ab=1/2cr+1/2br+1/2ar,
∴r=ab/(a+b+c).
方法二(利用切线长定理):
∵∠ODC=∠OEC=∠DCE=90°,
∴四边形ODCE是矩形.
∵OD=OE,
∴四边形ODCE是正方形.
由切线长定理可知,BD=BF,CD=CE=r,AE=AF,
a=BD+CD=BF+r,
b=AE+CE=AF+r,
c=AF+BF,
a+b - c=2r,
∴r=1/2(a+b - c).
故答案为1/2ab=1/2cr+1/2br+1/2ar;r=ab/(a+b+c);a+b - c=2r;r=1/2(a+b - c)
(2)相等.
理由如下:
∵a²+b²=c²,
∴(a+b+c)(a+b - c)=(a+b)² - c²=a²+2ab+b² - c²=2ab,
∴1/2(a+b - c)=ab/(a+b+c).

解:
(1)设D,E,F分别为切点.
方法一(面积法):如图,连结OA,OB,OC,OD,OE,OF,则OF⊥AB,OD⊥BC,OE⊥AC.
∵S△ABC=S△AOB+S△AOC+S△BOC,
∴1/2ab=1/2cr+1/2br+1/2ar,
∴r=ab/(a+b+c).
方法二(利用切线长定理):
∵∠ODC=∠OEC=∠DCE=90°,
∴四边形ODCE是矩形.
∵OD=OE,
∴四边形ODCE是正方形.
由切线长定理可知,BD=BF,CD=CE=r,AE=AF,
a=BD+CD=BF+r,
b=AE+CE=AF+r,
c=AF+BF,
a+b - c=2r,
∴r=1/2(a+b - c).
故答案为1/2ab=1/2cr+1/2br+1/2ar;r=ab/(a+b+c);a+b - c=2r;r=1/2(a+b - c)
(2)相等.
理由如下:
∵a²+b²=c²,
∴(a+b+c)(a+b - c)=(a+b)² - c²=a²+2ab+b² - c²=2ab,
∴1/2(a+b - c)=ab/(a+b+c).

查看更多完整答案,请扫码查看


