《2025年暑假乐园辽宁师范大学出版社七年级理综人教版》

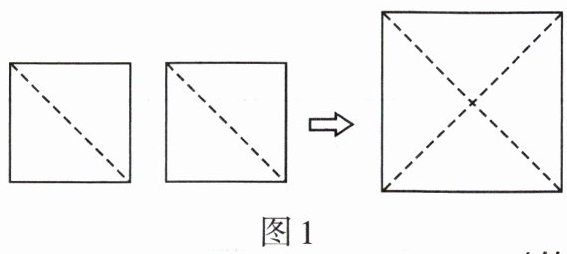
22. 【问题发现】如图 1，把两个面积都为 $1\mathrm{cm}^2$ 的小正方形分别沿对角线剪开，将所得的 4 个直角三角形拼成一个大正方形，则该大正方形的边长为$\sqrt{2}$cm.
【知识迁移】若一个圆与一个正方形的面积都是 $2\pi\mathrm{cm}^2$，设这个圆的周长为 $C_{\text{圆}}$，这个正方形的周长为 $C_{\text{正}}$，则 $C_{\text{圆}}$＜$C_{\text{正}}$.（填“＞”、“＜”或“=”）
【拓展延伸】李明想用一块面积为 $400\mathrm{cm}^2$ 的正方形纸片（如图 2 所示），沿着边的方向裁出一块面积为 $300\mathrm{cm}^2$ 的长方形纸片，使它的长与宽之比为 5:4. 请判断李明能否用这块纸片裁出符合要求的纸片，并说明理由.

答案： 【问题发现】$\sqrt{2}$ 【知识迁移】＜ 【拓展延伸】能，理由如下：设长方形的长为 $5x$ cm，则长方形的宽为 $4x$ cm。由题意，得 $5x \cdot 4x = 300$，则 $x = \sqrt{15}$，即长方形的长为 $5\sqrt{15}$ cm，宽为 $4\sqrt{15}$ cm。而面积为 $400 cm^2$ 的正方形的边长为 $\sqrt{400}$ cm，$5\sqrt{15} = \sqrt{375} ＜ \sqrt{400}$，所以能裁出一块面积为 $300 cm^2$ 的长方形纸片。

1. 阅读与思考
请阅读下面材料，并完成相应的任务.
在学习完实数的相关运算之后，某数学兴趣小组提出了一个有趣的问题：两个数的积的算术平方根与这两个数的算术平方根的积存在什么关系？小聪和小明分别用自己的方法进行了验证.
小聪：$\sqrt{4×25}=\sqrt{100}=10$，$\sqrt{4}×\sqrt{25}=2×5=10$. 所以 $\sqrt{4×25}=\sqrt{4}×\sqrt{25}$.
小明：$(\sqrt{4×25})^2=4×25=100$. $(\sqrt{4}×\sqrt{25})^2=(2×5)^2=100$. 这就说明 $\sqrt{4×25}$ 和 $\sqrt{4}×\sqrt{25}$ 都是 $4×25$ 的算术平方根，而 $4×25$ 的算术平方根只有一个，所以 $\sqrt{4×25}=\sqrt{4}×\sqrt{25}$.
任务：
（1）猜想：当 $a\geq0$，$b\geq0$ 时，$\sqrt{ab}$ 和 $\sqrt{a}×\sqrt{b}$ 之间存在怎样的关系，并仿照小聪或小明的方法举出一个例子进行说明.
猜想：当$a\geq0$，$b\geq0$时，$\sqrt{ab}=\sqrt{a}×\sqrt{b}$
例子：$\because\sqrt{4×9}=6$，$\sqrt{4}×\sqrt{9}=6$，$\therefore\sqrt{4×9}=\sqrt{4}×\sqrt{9}$
（2）运用以上结论计算：① $\sqrt{16×36}$；② $\sqrt{49×121}$.
① $\sqrt{16×36}=\sqrt{16}×\sqrt{36}=4×6=24$
② $\sqrt{49×121}=\sqrt{49}×\sqrt{121}=7×11=77$
（3）解决实际问题：已知一个长方形的长为 $\sqrt{100}$，宽为 $\sqrt{49}$，求这个长方形的面积.
解：$\because$长方形的长为$\sqrt{100}$，宽为$\sqrt{49}$，$\therefore S=\sqrt{100}×\sqrt{49}=70$
答：这个长方形的面积为70.

答案： 解：
(1) 当 $a \geq 0$，$b \geq 0$ 时，$\sqrt{ab} = \sqrt{a} × \sqrt{b}$。
例如：$\because \sqrt{4 × 9} = 6$，$\sqrt{4} × \sqrt{9} = 6$，$\therefore \sqrt{4 × 9} = \sqrt{4} × \sqrt{9}$。
(2) ① $\sqrt{16 × 36} = \sqrt{16} × \sqrt{36} = 4 × 6 = 24$。
② $\sqrt{49 × 121} = \sqrt{49} × \sqrt{121} = 7 × 11 = 77$。
(3) $\because$ 长方形的长为 $\sqrt{100}$，宽为 $\sqrt{49}$，$\therefore S = \sqrt{100} × \sqrt{49} = 70$。
答：这个长方形的面积为 70。