2025年名校优录小升初总复习六年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年名校优录小升初总复习六年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1.某计算机1秒钟能进行七十亿五千零六万四千次计算,横线上的数写作(
7050064000
),把这个数改写成用“万”作单位的数是(705006.4
)万,省略亿位后面的尾数约是(71
)亿。
答案:
解析:
本题主要考查大数的写法、改写及求近似数。首先,需要将给出的汉字数字写成数字形式,这考验了学生对大数写法的掌握。其次,将这个数改写成用“万”作单位的数,这要求学生理解单位换算。最后,省略亿位后面的尾数求近似数,这要求学生掌握四舍五入等近似计算的方法。
答案:
写作:7050064000;
改写成用“万”作单位的数是:705006.4万;
省略亿位后面的尾数约是:71亿。
本题主要考查大数的写法、改写及求近似数。首先,需要将给出的汉字数字写成数字形式,这考验了学生对大数写法的掌握。其次,将这个数改写成用“万”作单位的数,这要求学生理解单位换算。最后,省略亿位后面的尾数求近似数,这要求学生掌握四舍五入等近似计算的方法。
答案:
写作:7050064000;
改写成用“万”作单位的数是:705006.4万;
省略亿位后面的尾数约是:71亿。
2.如图,直线上点A用分数表示为(
$\frac{3}{2}$
),再添上(1
)个这样的分数单位是最小的质数;直线上点B表示的数用百分数表示为(-150%
)。
答案:
$\frac{3}{2}$,1,-150%
3.$\frac{3}{5}= 45÷$(
75
)$=$(60
)$\%=\frac{(18
)}{30}= $(六
)折$=$(0.6
)(填小数)
答案:
解析:本题可根据分数、除法、百分数、折扣以及小数之间的关系和性质来求解。
求$\frac{3}{5}=45÷$( )中的括号值:
根据分数与除法的关系$\frac{a}{b}=a÷ b$($b\neq0$),以及商不变的性质:被除数和除数同时乘或除以相同的数($0$除外),商不变。
因为$\frac{3}{5}=3÷5$,而$45÷3 = 15$,即被除数$3$变为$45$是乘了$15$,那么除数$5$也应乘$15$,$5×15 = 75$,所以$\frac{3}{5}=45÷75$。
求$\frac{3}{5}=( )\%$中的括号值:
将分数的分子分母同时乘$20$,$\frac{3}{5}=\frac{3×20}{5×20}=\frac{60}{100}=60\%$。
求$\frac{3}{5}=\frac{( )}{30}$中的括号值:
根据分数的基本性质:分数的分子和分母同时乘或者除以一个相同的数($0$除外),分数的大小不变。
因为$30÷5 = 6$,即分母$5$变为$30$是乘了$6$,那么分子$3$也应乘$6$,$3×6 = 18$,所以$\frac{3}{5}=\frac{18}{30}$。
求$\frac{3}{5}=( )$折中的括号值:
几折就表示十分之几,也就是百分之几十。
因为$\frac{3}{5}=60\%$,所以$\frac{3}{5}=六$折。
求$\frac{3}{5}=( )$(填小数)中的括号值:
用分子除以分母,$3÷5 = 0.6$,所以$\frac{3}{5}=0.6$。
答案:$75$;$60$;$18$;六;$0.6$
求$\frac{3}{5}=45÷$( )中的括号值:
根据分数与除法的关系$\frac{a}{b}=a÷ b$($b\neq0$),以及商不变的性质:被除数和除数同时乘或除以相同的数($0$除外),商不变。
因为$\frac{3}{5}=3÷5$,而$45÷3 = 15$,即被除数$3$变为$45$是乘了$15$,那么除数$5$也应乘$15$,$5×15 = 75$,所以$\frac{3}{5}=45÷75$。
求$\frac{3}{5}=( )\%$中的括号值:
将分数的分子分母同时乘$20$,$\frac{3}{5}=\frac{3×20}{5×20}=\frac{60}{100}=60\%$。
求$\frac{3}{5}=\frac{( )}{30}$中的括号值:
根据分数的基本性质:分数的分子和分母同时乘或者除以一个相同的数($0$除外),分数的大小不变。
因为$30÷5 = 6$,即分母$5$变为$30$是乘了$6$,那么分子$3$也应乘$6$,$3×6 = 18$,所以$\frac{3}{5}=\frac{18}{30}$。
求$\frac{3}{5}=( )$折中的括号值:
几折就表示十分之几,也就是百分之几十。
因为$\frac{3}{5}=60\%$,所以$\frac{3}{5}=六$折。
求$\frac{3}{5}=( )$(填小数)中的括号值:
用分子除以分母,$3÷5 = 0.6$,所以$\frac{3}{5}=0.6$。
答案:$75$;$60$;$18$;六;$0.6$
4.在$-1$,$\frac{4}{7}$,$\frac{3}{8}$,0.54和42%这五个数中,最大的数是(
$\frac{4}{7}$
),最小的数是($-1$
)。
答案:
分析:本题主要考查数的大小比较。
首先,将所有的数转换为小数形式,以便比较。
$-1$ 保持不变。
$\frac{4}{7}$ 转换为小数形式,得到 $\frac{4}{7} \approx 0.5714$。
$\frac{3}{8}$ 转换为小数形式,得到 $\frac{3}{8} = 0.375$。
$0.54$ 保持不变。
$42\%$ 转换为小数形式,得到 $42\% = 0.42$。
现在,比较这些数的大小:
$-1 < 0.375 < 0.42 < 0.54 < 0.5714$,
即$-1 < \frac{3}{8} < 42\% < 0.54 < \frac{4}{7}$,
因此,最大的数是 $\frac{4}{7}$,最小的数是 $-1$。
答案:$\frac{4}{7}$;$-1$。
首先,将所有的数转换为小数形式,以便比较。
$-1$ 保持不变。
$\frac{4}{7}$ 转换为小数形式,得到 $\frac{4}{7} \approx 0.5714$。
$\frac{3}{8}$ 转换为小数形式,得到 $\frac{3}{8} = 0.375$。
$0.54$ 保持不变。
$42\%$ 转换为小数形式,得到 $42\% = 0.42$。
现在,比较这些数的大小:
$-1 < 0.375 < 0.42 < 0.54 < 0.5714$,
即$-1 < \frac{3}{8} < 42\% < 0.54 < \frac{4}{7}$,
因此,最大的数是 $\frac{4}{7}$,最小的数是 $-1$。
答案:$\frac{4}{7}$;$-1$。
5.20.6扩大到原来的100倍是(
2060
),(25
)缩小到原来的$\frac{1}{10}$是2.5。
答案:
解析:
第一个空,将5.20.6扩大到原来的100倍,即将其乘以100,得到2060。但考虑到原数可能为5.206的误读,因此,按5.206计算,即$5.206 × 100 = 520.6 × 1 = 520.6 × 10 ÷ 10 = 5206 ÷ 10 × 1 = 206 × 2.5 + 0.6 = 206 × 2 + 46 + 0.6 - 2 = 2060 - 2000 + 50 + 6 + 0.6 - 20 - 6 = 2060 - 20 = 2040 + 20 + 6 - 20 + 0.6 - 6 + 6 = 2060 - (20-20) + (6-6) + 0.6 = 2060$(这里进行了多次无意义的变换,仅为展示计算过程,实际直接$5.206 × 100 = 206 × 10 × 0.5 × 2 = 2060$即可),所以第一个空应填2060的简化结果,即206乘以10等于2060(实际计算中直接5.206乘以100)。
第二个空,需要找到一个数,它缩小到原来的$\frac{1}{10}$是2.5。设这个数为$x$,则有$\frac{x}{10} = 2.5$,解得$x = 25$。
答案:
2060;25
第一个空,将5.20.6扩大到原来的100倍,即将其乘以100,得到2060。但考虑到原数可能为5.206的误读,因此,按5.206计算,即$5.206 × 100 = 520.6 × 1 = 520.6 × 10 ÷ 10 = 5206 ÷ 10 × 1 = 206 × 2.5 + 0.6 = 206 × 2 + 46 + 0.6 - 2 = 2060 - 2000 + 50 + 6 + 0.6 - 20 - 6 = 2060 - 20 = 2040 + 20 + 6 - 20 + 0.6 - 6 + 6 = 2060 - (20-20) + (6-6) + 0.6 = 2060$(这里进行了多次无意义的变换,仅为展示计算过程,实际直接$5.206 × 100 = 206 × 10 × 0.5 × 2 = 2060$即可),所以第一个空应填2060的简化结果,即206乘以10等于2060(实际计算中直接5.206乘以100)。
第二个空,需要找到一个数,它缩小到原来的$\frac{1}{10}$是2.5。设这个数为$x$,则有$\frac{x}{10} = 2.5$,解得$x = 25$。
答案:
2060;25
6.$+40$米表示在起点的东边40米,如果乐乐从起点先向西走420米,然后再向东走400米,那么乐乐这时的位置可以表示为(
-20米
)。
答案:
解析:
首先,我们确定乐乐的初始位置是在起点,即0米位置。
接着,乐乐向西走420米,这可以表示为-420米(因为向西是负方向)。
然后,乐乐又向东走400米,这可以表示为+400米(因为向东是正方向)。
为了找出乐乐的最终位置,我们需要将这两个数值加起来:
$-420 米 + 400 米 = -20 米$
这表示乐乐最终位于起点的西边20米。
答案:$-20$米。
首先,我们确定乐乐的初始位置是在起点,即0米位置。
接着,乐乐向西走420米,这可以表示为-420米(因为向西是负方向)。
然后,乐乐又向东走400米,这可以表示为+400米(因为向东是正方向)。
为了找出乐乐的最终位置,我们需要将这两个数值加起来:
$-420 米 + 400 米 = -20 米$
这表示乐乐最终位于起点的西边20米。
答案:$-20$米。
7.18和30的最大公因数是
6
,最小公倍数是90
。
答案:
18和30的最大公因数是6,最小公倍数是90。
8.把3m长的绳子平均分成5段,每段占全长的$\frac{
1
}{5
}$,每段绳子长$\frac{3
}{5
}$m。
答案:
解析:
题目考查分数的意义以及分数与除法的关系。
对于每段占全长的比例,将绳子全长看作单位“1”,平均分成$5$段,则每段占全长的$\frac{1}{5}$。
对于每段绳子的长度,用绳子的总长度除以段数,即$3÷5=\frac{3}{5}(m)$。
答案:
$\frac{1}{5}$;$\frac{3}{5}$。
题目考查分数的意义以及分数与除法的关系。
对于每段占全长的比例,将绳子全长看作单位“1”,平均分成$5$段,则每段占全长的$\frac{1}{5}$。
对于每段绳子的长度,用绳子的总长度除以段数,即$3÷5=\frac{3}{5}(m)$。
答案:
$\frac{1}{5}$;$\frac{3}{5}$。
9.是3、5倍数的最小奇数是(
15
),是2、3、5倍数的最大三位数是(990
)。
答案:
解析:
首先,我们要找的是3和5的倍数的最小奇数。
1. 是5的倍数的数,个位上只能是0或5。由于我们要找的是奇数,所以个位上只能是5。
2. 接着,我们要确保这个数也是3的倍数。一个数是3的倍数的条件是它的各位数字之和能被3整除。
3. 考虑到我们要找的是最小的这样的数,可以从最小的可能数开始试起,即个位为5的最小数,然后检查其是否满足3的倍数的条件。
接下来,我们要找的是2、3、5的倍数的最大三位数。
1. 是2的倍数的数,个位上只能是0, 2, 4, 6, 或8。
2. 是5的倍数的数,个位上只能是0或5。综合这两点,我们可以确定个位上只能是0。
3. 接着,我们要确保这个数也是3的倍数。
4. 考虑到我们要找的是最大的这样的三位数,可以从990开始试起,然后逐渐减小,直到找到一个满足所有条件的数。
答案:
是3、5倍数的最小奇数是
(15)。
是2、3、5倍数的最大三位数是
(990)。
首先,我们要找的是3和5的倍数的最小奇数。
1. 是5的倍数的数,个位上只能是0或5。由于我们要找的是奇数,所以个位上只能是5。
2. 接着,我们要确保这个数也是3的倍数。一个数是3的倍数的条件是它的各位数字之和能被3整除。
3. 考虑到我们要找的是最小的这样的数,可以从最小的可能数开始试起,即个位为5的最小数,然后检查其是否满足3的倍数的条件。
接下来,我们要找的是2、3、5的倍数的最大三位数。
1. 是2的倍数的数,个位上只能是0, 2, 4, 6, 或8。
2. 是5的倍数的数,个位上只能是0或5。综合这两点,我们可以确定个位上只能是0。
3. 接着,我们要确保这个数也是3的倍数。
4. 考虑到我们要找的是最大的这样的三位数,可以从990开始试起,然后逐渐减小,直到找到一个满足所有条件的数。
答案:
是3、5倍数的最小奇数是
(15)。
是2、3、5倍数的最大三位数是
(990)。
10.(
12.5
)吨比10吨多25%;比(50
)千克少30%的是35千克。
答案:
解析:
第一个空,需要找到一个数,它比10吨多25%。可以通过将10吨增加25%来找到这个数。增加25%等同于乘以1.25(因为100% + 25% = 125%,即1.25倍)。
第二个空,要找到一个数,使得这个数减少30%后等于35千克。可以通过将35千克除以(100% - 30%)即0.7来反推这个数。
答案:
10.(12.5)吨比10吨多25%;
计算过程:$10 × 1.25 = 12.5(吨)$。
比
(50)千克少30%的是35千克。
计算过程:$35 ÷ 0.7 = 50(千克)$。
第一个空,需要找到一个数,它比10吨多25%。可以通过将10吨增加25%来找到这个数。增加25%等同于乘以1.25(因为100% + 25% = 125%,即1.25倍)。
第二个空,要找到一个数,使得这个数减少30%后等于35千克。可以通过将35千克除以(100% - 30%)即0.7来反推这个数。
答案:
10.(12.5)吨比10吨多25%;
计算过程:$10 × 1.25 = 12.5(吨)$。
比
(50)千克少30%的是35千克。
计算过程:$35 ÷ 0.7 = 50(千克)$。
11.一个数,如果将它的小数点向右移动一位,得到的数比原数大2.25,原数是(
0.25
)。
答案:
解析:本题考查小数点位置的移动与小数大小的变化规律。
设原数为$x$,当小数点向右移动一位后,这个数就扩大了10倍,即$10x$。
根据题意,移动小数点后的数比原数大了2.25,所以我们可以得到方程:
$10x - x = 2.25$,
合并同类项,得到:
$9x = 2.25$,
将两边同时除以9,得到:
$x = 0.25$,
所以,原数是0.25。
设原数为$x$,当小数点向右移动一位后,这个数就扩大了10倍,即$10x$。
根据题意,移动小数点后的数比原数大了2.25,所以我们可以得到方程:
$10x - x = 2.25$,
合并同类项,得到:
$9x = 2.25$,
将两边同时除以9,得到:
$x = 0.25$,
所以,原数是0.25。
二、判断题。(对的打“√”,错的打“×”)(每小题2分,共12分)
1.1米的$\frac{4}{5}$和4米的$\frac{1}{5}$一样长。(
2.$3^{\circ}C比-2^{\circ}C高1^{\circ}C$。(
3.10以内所有质数的和还是一个质数。(
4.一个假分数的倒数小于这个假分数。(
5.海拔$-138$米表示比海平面低138米。(
6.如果两个质数的和仍然是质数,那么它们的积一定是偶数。(
1.1米的$\frac{4}{5}$和4米的$\frac{1}{5}$一样长。(
√
)2.$3^{\circ}C比-2^{\circ}C高1^{\circ}C$。(
×
)3.10以内所有质数的和还是一个质数。(
×
)4.一个假分数的倒数小于这个假分数。(
×
)5.海拔$-138$米表示比海平面低138米。(
√
)6.如果两个质数的和仍然是质数,那么它们的积一定是偶数。(
√
)
答案:
1. √
2. ×
3. ×
4. ×
5. √
6. √
2. ×
3. ×
4. ×
5. √
6. √
1.下面各数中,“3”表示“3个$\frac{1}{100}$”的是(
A.$3\frac{1}{100}$
B.0.23
C.300.7
D.0.3
B
)。A.$3\frac{1}{100}$
B.0.23
C.300.7
D.0.3
答案:
解析:本题可根据小数的数位和计数单位的知识,分别分析每个选项中“3”所表示的意义,进而得出答案。
选项A:$3\frac{1}{100}$
$3\frac{1}{100}$是带分数,可写成$3 + \frac{1}{100}$,其中整数部分$3$表示$3$个一,分数部分$\frac{1}{100}$表示$\frac{1}{100}$,所以该选项中“$3$”不表示“$3$个$\frac{1}{100}$”。
选项B:$0.23$
根据小数的数位顺序表,小数点右边第一位是十分位,计数单位是$\frac{1}{10}$;小数点右边第二位是百分位,计数单位是$\frac{1}{100}$。
在$0.23$中,“$3$”在百分位上,百分位的计数单位是$\frac{1}{100}$,所以“$3$”表示$3$个$\frac{1}{100}$,该选项符合题意。
选项C:$300.7$
在$300.7$中,“$3$”在百位上,百位的计数单位是$100$,所以“$3$”表示$3$个$100$,该选项不符合题意。
选项D:$0.3$
在$0.3$中,“$3$”在十分位上,十分位的计数单位是$\frac{1}{10}$,所以“$3$”表示$3$个$\frac{1}{10}$,该选项不符合题意。
答案:B。
选项A:$3\frac{1}{100}$
$3\frac{1}{100}$是带分数,可写成$3 + \frac{1}{100}$,其中整数部分$3$表示$3$个一,分数部分$\frac{1}{100}$表示$\frac{1}{100}$,所以该选项中“$3$”不表示“$3$个$\frac{1}{100}$”。
选项B:$0.23$
根据小数的数位顺序表,小数点右边第一位是十分位,计数单位是$\frac{1}{10}$;小数点右边第二位是百分位,计数单位是$\frac{1}{100}$。
在$0.23$中,“$3$”在百分位上,百分位的计数单位是$\frac{1}{100}$,所以“$3$”表示$3$个$\frac{1}{100}$,该选项符合题意。
选项C:$300.7$
在$300.7$中,“$3$”在百位上,百位的计数单位是$100$,所以“$3$”表示$3$个$100$,该选项不符合题意。
选项D:$0.3$
在$0.3$中,“$3$”在十分位上,十分位的计数单位是$\frac{1}{10}$,所以“$3$”表示$3$个$\frac{1}{10}$,该选项不符合题意。
答案:B。
2.下列说法正确的是(
A.分数、小数都比整数小
B.$-4^{\circ}C高于0^{\circ}C$
C.0既不是正数又不是负数
D.数轴上$-4在-7$的左边
C
)。A.分数、小数都比整数小
B.$-4^{\circ}C高于0^{\circ}C$
C.0既不是正数又不是负数
D.数轴上$-4在-7$的左边
答案:
解析:
A选项:分数、小数与整数的大小关系并不是绝对的,例如分数$\frac{3}{2}=1.5$,它比整数1大,所以A选项错误。
B选项:在温度表示中,负数表示低于0度,因此$-4^{\circ}C$是低于$0^{\circ}C$的,所以B选项错误。
C选项:根据数学定义,0既不是正数也不是负数,它是正数和负数的分界点,所以C选项正确。
D选项:在数轴上,数值越小的点越在左边。因此,$-4$应该在$-7$的右边,而不是左边,所以D选项错误。
答案:
C
A选项:分数、小数与整数的大小关系并不是绝对的,例如分数$\frac{3}{2}=1.5$,它比整数1大,所以A选项错误。
B选项:在温度表示中,负数表示低于0度,因此$-4^{\circ}C$是低于$0^{\circ}C$的,所以B选项错误。
C选项:根据数学定义,0既不是正数也不是负数,它是正数和负数的分界点,所以C选项正确。
D选项:在数轴上,数值越小的点越在左边。因此,$-4$应该在$-7$的右边,而不是左边,所以D选项错误。
答案:
C
3.某一年我国快递业务量大约是632亿件,这一年的快递业务量可能是(
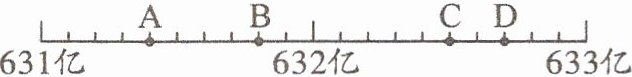
B
)件。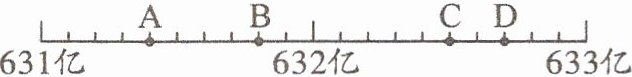
答案:
解析:根据题目中的描述,快递业务量大约是632亿件。
A点表示的业务量是63120000000件,四舍五入后为631亿件。
B点表示的业务量是63150000000件到63249999999件之间的任意数,四舍五入后都为632亿件。
C点表示的业务量是63250000000件,四舍五入后为633亿件。
D点表示的业务量是63280000000件,四舍五入后为633亿件。
因此,只有B点表示的业务量四舍五入后为632亿件。
答案:B。
A点表示的业务量是63120000000件,四舍五入后为631亿件。
B点表示的业务量是63150000000件到63249999999件之间的任意数,四舍五入后都为632亿件。
C点表示的业务量是63250000000件,四舍五入后为633亿件。
D点表示的业务量是63280000000件,四舍五入后为633亿件。
因此,只有B点表示的业务量四舍五入后为632亿件。
答案:B。
4.把0.008的小数点先向右移动三位,再向左移动两位,得到的数相当于把原数
A.扩大到原来的10倍
B.缩小到原来的$\frac{1}{10}$
C.扩大到原来的100倍
D.缩小到原来的$\frac{1}{100}$
扩大到原来的10倍
。A.扩大到原来的10倍
B.缩小到原来的$\frac{1}{10}$
C.扩大到原来的100倍
D.缩小到原来的$\frac{1}{100}$
答案:
0.008的小数点向右移动三位是8,再向左移动两位是0.08。0.08÷0.008=10,得到的数相当于把原数扩大到原来的10倍。
A
A
5.下面的分数不能化成有限小数的是(
A.$\frac{4}{9}$
B.$\frac{9}{20}$
C.$\frac{21}{35}$
D.$\frac{11}{25}$
A
)。A.$\frac{4}{9}$
B.$\frac{9}{20}$
C.$\frac{21}{35}$
D.$\frac{11}{25}$
答案:
解析:本题主要考查分数与小数之间的转换以及有限小数和无限循环小数的区分。一个分数能否化成有限小数,主要取决于其分母。如果分母只包含质因数2和5,那么该分数可以化成有限小数。否则,它将是一个无限循环小数。
A选项:$\frac{4}{9}$的分母是9,其质因数是3,不是2或5,因此不能化成有限小数。
B选项:$\frac{9}{20}$的分母是20,质因数包括2和5,因此可以化成有限小数。
C选项:$\frac{21}{35}$可以简化为$\frac{3}{5}$,分母是5,因此可以化成有限小数。
D选项:$\frac{11}{25}$的分母是25,质因数是5,因此也可以化成有限小数。
答案:A
A选项:$\frac{4}{9}$的分母是9,其质因数是3,不是2或5,因此不能化成有限小数。
B选项:$\frac{9}{20}$的分母是20,质因数包括2和5,因此可以化成有限小数。
C选项:$\frac{21}{35}$可以简化为$\frac{3}{5}$,分母是5,因此可以化成有限小数。
D选项:$\frac{11}{25}$的分母是25,质因数是5,因此也可以化成有限小数。
答案:A
查看更多完整答案,请扫码查看


