2025年名校优录小升初总复习六年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年名校优录小升初总复习六年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
| | | | |
| a |
| b | 26 |
| a |
18
| 23.5 | 24
|| b | 26 |
37
| 38 |
答案:
解析:本题考查了运用字母表示数及代入求值。
当$b = 26$时:
$26 = 2a - 10$,
$2a = 26 + 10$,
$2a = 36$,
$a = 18$。
当$a = 23.5$时:
$b = 2×23.5 - 10$,
$b = 47 - 10$,
$b = 37$。
当$b = 38$时:
$38 = 2a - 10$,
$2a = 38 + 10$,
$2a = 48$,
$a = 24$。
答案:18;37;24。
当$b = 26$时:
$26 = 2a - 10$,
$2a = 26 + 10$,
$2a = 36$,
$a = 18$。
当$a = 23.5$时:
$b = 2×23.5 - 10$,
$b = 47 - 10$,
$b = 37$。
当$b = 38$时:
$38 = 2a - 10$,
$2a = 38 + 10$,
$2a = 48$,
$a = 24$。
答案:18;37;24。
五、求出下面式子的值。
1.当$a= 7.6$,$b= 0.8$时,求$a+2b和3(a-2b)$的值。
2.当$a= 0.2$,$b= 0.7$,$c= 1.4$时,求$a^{2}+c-b^{2}$的值。
1.当$a= 7.6$,$b= 0.8$时,求$a+2b和3(a-2b)$的值。
2.当$a= 0.2$,$b= 0.7$,$c= 1.4$时,求$a^{2}+c-b^{2}$的值。
答案:
1.
解析:本题需要将给定的$a$和$b$的值代入到式子$a+2b$和$3(a-2b)$中进行计算。
对于$a+2b$:
将$a=7.6$,$b=0.8$代入得:
$a+2b$
$=7.6+2× 0.8$
$=7.6+1.6$
$=9.2$
对于$3(a-2b)$:
将$a=7.6$,$b=0.8$代入得:
$3(a-2b)$
$=3×(7.6-2× 0.8)$
$=3×(7.6-1.6)$
$=3× 6$
$=18$
答案:$a+2b=9.2$,$3(a-2b)=18$。
2.
解析:本题需要将给定的$a$,$b$和$c$的值代入到式子$a^{2}+c-b^{2}$中进行计算。
将$a=0.2$,$b=0.7$,$c=1.4$代入得:
$a^{2}+c-b^{2}$
$=0.2^{2}+1.4-0.7^{2}$
$=0.04+1.4-0.49$
$=1.44-0.49$
$=0.95$
答案:$a^{2}+c-b^{2}=0.95$。
解析:本题需要将给定的$a$和$b$的值代入到式子$a+2b$和$3(a-2b)$中进行计算。
对于$a+2b$:
将$a=7.6$,$b=0.8$代入得:
$a+2b$
$=7.6+2× 0.8$
$=7.6+1.6$
$=9.2$
对于$3(a-2b)$:
将$a=7.6$,$b=0.8$代入得:
$3(a-2b)$
$=3×(7.6-2× 0.8)$
$=3×(7.6-1.6)$
$=3× 6$
$=18$
答案:$a+2b=9.2$,$3(a-2b)=18$。
2.
解析:本题需要将给定的$a$,$b$和$c$的值代入到式子$a^{2}+c-b^{2}$中进行计算。
将$a=0.2$,$b=0.7$,$c=1.4$代入得:
$a^{2}+c-b^{2}$
$=0.2^{2}+1.4-0.7^{2}$
$=0.04+1.4-0.49$
$=1.44-0.49$
$=0.95$
答案:$a^{2}+c-b^{2}=0.95$。
1.参照下面的标准,用含有字母的式子表示出少年儿童(7~16岁)的标准体重,再通过计算说明小明的体重处于何种状态。(标准体重和年龄分别用a和b表示)
| 少年儿童(7~16岁)体重(千克)分类标准 |
| 标准体重= 年龄×2+8 |
| 轻度肥胖:超过标准体重20%~30% |
| 中度肥胖:超过标准体重30%~50% |
| 重度肥胖:超过标准体重50%以上 |

| 少年儿童(7~16岁)体重(千克)分类标准 |
| 标准体重= 年龄×2+8 |
| 轻度肥胖:超过标准体重20%~30% |
| 中度肥胖:超过标准体重30%~50% |
| 重度肥胖:超过标准体重50%以上 |

答案:
标准体重为:$a = 2b + 8$。
小明$12$岁,将$b = 12$带入式子得小明的标准体重为:
$2 × 12 + 8$
$= 24 + 8$
$= 32$(千克)
小明实际体重为$40$千克,计算小明体重超过标准体重的百分比:
$\frac{40 - 32}{32} × 100\%$
$= \frac{8}{32} × 100\%$
$= 25\%$
轻度肥胖范围是超过标准体重$20\% \sim 30\%$,$20\%<25\%<30\%$,所以小明处于轻度肥胖状态。
综上,式子为$a = 2b + 8$;小明处于轻度肥胖状态。
小明$12$岁,将$b = 12$带入式子得小明的标准体重为:
$2 × 12 + 8$
$= 24 + 8$
$= 32$(千克)
小明实际体重为$40$千克,计算小明体重超过标准体重的百分比:
$\frac{40 - 32}{32} × 100\%$
$= \frac{8}{32} × 100\%$
$= 25\%$
轻度肥胖范围是超过标准体重$20\% \sim 30\%$,$20\%<25\%<30\%$,所以小明处于轻度肥胖状态。
综上,式子为$a = 2b + 8$;小明处于轻度肥胖状态。
2.下面是贝贝设计的一个计算程序。

(1)甜甜输入a,那么输出的数是多少?
(2)当丽丽输入的数是52时,输出的数是多少?

(1)甜甜输入a,那么输出的数是多少?
(2)当丽丽输入的数是52时,输出的数是多少?
答案:
解析:本题可根据所给计算程序,结合用字母表示数以及四则运算的规则来求解。
(1)甜甜输入$a$,根据计算程序,先乘$0.25$,得到$0.25a$,再减去$3$,所以输出的数是$0.25a - 3$。
(2)当丽丽输入的数是$52$时,同样按照计算程序,先乘$0.25$,即$52×0.25 = 13$,再减去$3$,$13 - 3 = 10$,所以输出的数是$10$。
答案:
(1)$0.25a - 3$;
(2)$10$。
(1)甜甜输入$a$,根据计算程序,先乘$0.25$,得到$0.25a$,再减去$3$,所以输出的数是$0.25a - 3$。
(2)当丽丽输入的数是$52$时,同样按照计算程序,先乘$0.25$,即$52×0.25 = 13$,再减去$3$,$13 - 3 = 10$,所以输出的数是$10$。
答案:
(1)$0.25a - 3$;
(2)$10$。
3.修一段公路,已经修了12天,每天修a米,还剩300米没有修。
(1)请用含字母的式子表示这段公路的长度。
(2)如果$a= 150$,求这段公路的长度是多少。
(1)请用含字母的式子表示这段公路的长度。
(2)如果$a= 150$,求这段公路的长度是多少。
答案:
解析:
(1) 题目考查的是用字母表示数的能力以及基本的代数表达式构建。需要理解题目中的信息,并将其转化为数学表达式。
首先,已经修了的公路长度是 $12 × a$ 米(每天修的长度乘以天数)。
其次,还剩300米没有修。
因此,整段公路的长度应该是已经修了的长度加上还未修的长度,即 $(12a + 300)$ 米。
(2) 题目考查代数表达式的求值。
给定 $a = 150$,需要将其代入到 $(12a + 300)$ 中进行计算。
答案:
(1) 这段公路的长度为 $(12a + 300)$ 米。
(2) 当 $a = 150$ 时,公路的长度为:
$12 × 150 + 300 = 1800 + 300 = 2100 (米)$
答:这段公路的长度是2100米。
(1) 题目考查的是用字母表示数的能力以及基本的代数表达式构建。需要理解题目中的信息,并将其转化为数学表达式。
首先,已经修了的公路长度是 $12 × a$ 米(每天修的长度乘以天数)。
其次,还剩300米没有修。
因此,整段公路的长度应该是已经修了的长度加上还未修的长度,即 $(12a + 300)$ 米。
(2) 题目考查代数表达式的求值。
给定 $a = 150$,需要将其代入到 $(12a + 300)$ 中进行计算。
答案:
(1) 这段公路的长度为 $(12a + 300)$ 米。
(2) 当 $a = 150$ 时,公路的长度为:
$12 × 150 + 300 = 1800 + 300 = 2100 (米)$
答:这段公路的长度是2100米。
4.如下图所示,在长方形内截取一个最大的正方形,阴影表示剩余部分。
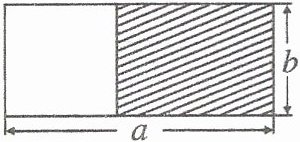
(1)用含有字母的式子表示阴影部分的周长。
(2)用含有字母的式子表示阴影部分的面积。
(3)当$a= 5.5$,$b= 2$时,则阴影部分的周长和面积各是多少?

(1)用含有字母的式子表示阴影部分的周长。
(2)用含有字母的式子表示阴影部分的面积。
(3)当$a= 5.5$,$b= 2$时,则阴影部分的周长和面积各是多少?
答案:
(1)观察图形可知,长方形的长为$a$,宽为$b$,在长方形中截取一个最大的正方形,正方形的边长为长方形的宽$b$,那么剩余部分(阴影部分)为一个长方形,其长为$b$,宽为$(a - b)$。
根据长方形周长公式$C=(长 + 宽)×2$,可得阴影部分周长$C = 2×(b + a - b)=2a$。
答:阴影部分的周长为$2a$。
(2)根据长方形面积公式$S = 长×宽$,可得阴影部分面积$S = b×(a - b)=ab - b^{2}$。
答:阴影部分的面积为$ab - b^{2}$。
(3)当$a = 5.5$,$b = 2$时,
阴影部分周长$C = 2a = 2×5.5 = 11$;
阴影部分面积$S = ab - b^{2}=5.5×2 - 2^{2}=11 - 4 = 7$。
答:阴影部分的周长是$11$,面积是$7$。
(1)观察图形可知,长方形的长为$a$,宽为$b$,在长方形中截取一个最大的正方形,正方形的边长为长方形的宽$b$,那么剩余部分(阴影部分)为一个长方形,其长为$b$,宽为$(a - b)$。
根据长方形周长公式$C=(长 + 宽)×2$,可得阴影部分周长$C = 2×(b + a - b)=2a$。
答:阴影部分的周长为$2a$。
(2)根据长方形面积公式$S = 长×宽$,可得阴影部分面积$S = b×(a - b)=ab - b^{2}$。
答:阴影部分的面积为$ab - b^{2}$。
(3)当$a = 5.5$,$b = 2$时,
阴影部分周长$C = 2a = 2×5.5 = 11$;
阴影部分面积$S = ab - b^{2}=5.5×2 - 2^{2}=11 - 4 = 7$。
答:阴影部分的周长是$11$,面积是$7$。
查看更多完整答案,请扫码查看


