2025年名校优录小升初总复习六年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年名校优录小升初总复习六年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 一个三角形的两个角都是40度,那么第三个角是(
100
)度。如果按角分,这个三角形是(钝角
)三角形;如果按边分,这个三角形是(等腰
)三角形。
答案:
解析:首先,根据三角形内角和为$180$度的性质,可以求出第三个角的度数。已知两个角都是$40$度,所以第三个角的度数为$180 - 40 × 2 = 100$(度)。
然后,根据三角形的分类来判断这个三角形的类型。按角分,由于第三个角是$100$度,是钝角,所以这个三角形是钝角三角形。
按边分,由于有两个角相等,根据等腰三角形的性质,等角对等边,所以这个三角形有两条边相等,是等腰三角形。
答案:$100$;钝角;等腰。
然后,根据三角形的分类来判断这个三角形的类型。按角分,由于第三个角是$100$度,是钝角,所以这个三角形是钝角三角形。
按边分,由于有两个角相等,根据等腰三角形的性质,等角对等边,所以这个三角形有两条边相等,是等腰三角形。
答案:$100$;钝角;等腰。
2. 一个圆柱形橡皮泥,底面积是$37.68 cm^2,$高是6 cm。如果把它捏成等底的圆锥,这个圆锥的高是(
18
)cm;如果把它捏成等高的圆锥,这个圆锥的底面积是(113.04
)$cm^2$。
答案:
解析:
本题考查的是圆柱和圆锥的体积公式。
圆柱的体积公式是 $V = S× h$,其中 S 是底面积,h 是高。
圆锥的体积公式是 $V = \frac{1}{3}× S × h$,其中 S 是底面积,h 是高。
首先,计算圆柱形橡皮泥的体积。
已知圆柱形橡皮泥的底面积是 $37.68 cm^2$,高是 6 cm,
所以,$V = 37.68 × 6 = 226.08(cm^3)$。
如果把它捏成等底的圆锥,则圆锥的底面积也是 $37.68 cm^2$。
设圆锥的高为 h,由于圆锥的体积等于圆柱的体积,
所以有 $\frac{1}{3} × 37.68 × h = 226.08$,
解这个方程,得到 $h = 18 cm$。
如果把它捏成等高的圆锥,则圆锥的高也是 6 cm。
设圆锥的底面积为 S,由于圆锥的体积等于圆柱的体积,
所以有 $\frac{1}{3} × S × 6 = 226.08$,
解这个方程,得到 $S = 113.04 cm^2$。
答案:18;113.04。
本题考查的是圆柱和圆锥的体积公式。
圆柱的体积公式是 $V = S× h$,其中 S 是底面积,h 是高。
圆锥的体积公式是 $V = \frac{1}{3}× S × h$,其中 S 是底面积,h 是高。
首先,计算圆柱形橡皮泥的体积。
已知圆柱形橡皮泥的底面积是 $37.68 cm^2$,高是 6 cm,
所以,$V = 37.68 × 6 = 226.08(cm^3)$。
如果把它捏成等底的圆锥,则圆锥的底面积也是 $37.68 cm^2$。
设圆锥的高为 h,由于圆锥的体积等于圆柱的体积,
所以有 $\frac{1}{3} × 37.68 × h = 226.08$,
解这个方程,得到 $h = 18 cm$。
如果把它捏成等高的圆锥,则圆锥的高也是 6 cm。
设圆锥的底面积为 S,由于圆锥的体积等于圆柱的体积,
所以有 $\frac{1}{3} × S × 6 = 226.08$,
解这个方程,得到 $S = 113.04 cm^2$。
答案:18;113.04。
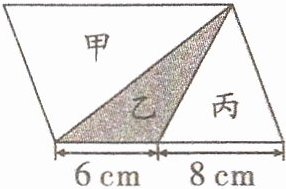
3.(贵州六盘水)右图中的平行四边形的面积是$98 cm^2,$丙三角形的面积是甲三角形的(
4
)/(7
),涂色部分的面积是(28
)$cm^2。$
答案:
解析:本题主要考查平行四边形和三角形的面积公式,通过已知条件求出相关三角形的面积,进而求出面积比例和涂色部分面积。
1. 求甲三角形的面积:
已知平行四边形面积是$98cm^2$,甲三角形与平行四边形等底等高,根据三角形面积公式$S = \frac{1}{2}ah$($a$为底,$h$为高),平行四边形面积公式$S = ah$,可知甲三角形面积是平行四边形面积的一半,即$98÷2 = 49cm^2$。
2. 求丙三角形的面积:
设平行四边形的高为$h$,根据平行四边形面积公式$S = ah$($a$为底),已知平行四边形面积是$98cm^2$,底为$(6 + 8)cm$,则$h=\frac{98}{6 + 8}=7cm$。
丙三角形底为$8cm$,高为$7cm$,根据三角形面积公式可得丙三角形面积为$\frac{1}{2}×8×7 = 28cm^2$。
3. 求丙三角形面积是甲三角形面积的几分之几:
用丙三角形面积除以甲三角形面积,即$\frac{28}{49}=\frac{4}{7}$。
4. 求涂色部分面积:
观察图形可知,涂色部分面积等于丙三角形面积,为$28cm^2$。
答案:$\frac{4}{7}$;$28$。
1. 求甲三角形的面积:
已知平行四边形面积是$98cm^2$,甲三角形与平行四边形等底等高,根据三角形面积公式$S = \frac{1}{2}ah$($a$为底,$h$为高),平行四边形面积公式$S = ah$,可知甲三角形面积是平行四边形面积的一半,即$98÷2 = 49cm^2$。
2. 求丙三角形的面积:
设平行四边形的高为$h$,根据平行四边形面积公式$S = ah$($a$为底),已知平行四边形面积是$98cm^2$,底为$(6 + 8)cm$,则$h=\frac{98}{6 + 8}=7cm$。
丙三角形底为$8cm$,高为$7cm$,根据三角形面积公式可得丙三角形面积为$\frac{1}{2}×8×7 = 28cm^2$。
3. 求丙三角形面积是甲三角形面积的几分之几:
用丙三角形面积除以甲三角形面积,即$\frac{28}{49}=\frac{4}{7}$。
4. 求涂色部分面积:
观察图形可知,涂色部分面积等于丙三角形面积,为$28cm^2$。
答案:$\frac{4}{7}$;$28$。
4. 用长4厘米、宽2厘米、高1厘米的长方体木块拼成一个正方体,至少要用(
8
)个这样的长方体。拼成的正方体的表面积是(96
)平方厘米。
答案:
要拼成正方体,正方体的棱长应是长方体长、宽、高的最小公倍数。
4、2、1的最小公倍数是4,即正方体棱长为4厘米。
沿长摆:4÷4=1(个)
沿宽摆:4÷2=2(个)
沿高摆:4÷1=4(个)
至少需要长方体木块:1×2×4=8(个)
拼成的正方体表面积:4×4×6=96(平方厘米)
8;96
4、2、1的最小公倍数是4,即正方体棱长为4厘米。
沿长摆:4÷4=1(个)
沿宽摆:4÷2=2(个)
沿高摆:4÷1=4(个)
至少需要长方体木块:1×2×4=8(个)
拼成的正方体表面积:4×4×6=96(平方厘米)
8;96
5. 在一个正方形里面画一个最大的圆,这个圆的周长是6.28 cm,这个正方形的面积是$(
4
)cm^2,$剩下的面积是$(0.86
)cm^2。$
答案:
圆的直径:$6.28÷3.14 = 2\,cm$
正方形边长等于圆的直径,即$2\,cm$
正方形面积:$2×2 = 4\,cm^2$
圆的半径:$2÷2 = 1\,cm$
圆的面积:$3.14×1^2 = 3.14\,cm^2$
剩下的面积:$4 - 3.14 = 0.86\,cm^2$
4,0.86
正方形边长等于圆的直径,即$2\,cm$
正方形面积:$2×2 = 4\,cm^2$
圆的半径:$2÷2 = 1\,cm$
圆的面积:$3.14×1^2 = 3.14\,cm^2$
剩下的面积:$4 - 3.14 = 0.86\,cm^2$
4,0.86
6. 一个长方体的棱长总和是72 cm,它的长、宽、高的比是4∶3∶2,它的表面积是
208
$cm^2,$体积是192
$cm^3。$
答案:
72÷4=18(cm)
4+3+2=9
长:18×4/9=8(cm)
宽:18×3/9=6(cm)
高:18×2/9=4(cm)
表面积:(8×6+8×4+6×4)×2=208(cm²)
体积:8×6×4=192(cm³)
208,192
4+3+2=9
长:18×4/9=8(cm)
宽:18×3/9=6(cm)
高:18×2/9=4(cm)
表面积:(8×6+8×4+6×4)×2=208(cm²)
体积:8×6×4=192(cm³)
208,192
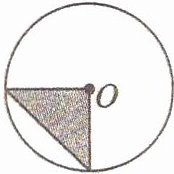
7. 如图,直角三角形的面积是$3 cm^2,$圆的面积是$( )cm^2。$

答案:
解析:
首先,我们设圆的半径为$r$,由于直角三角形的两条直角边都是圆的半径,所以其面积为$\frac{1}{2}r^2 = 3$,
解这个方程,我们得到$r^2 = 6$,
圆的面积公式为$\pi r^2$,将$r^2 = 6$代入,得到圆的面积为$6\pi$ $cm^2$。
答案:$6\pi$。
首先,我们设圆的半径为$r$,由于直角三角形的两条直角边都是圆的半径,所以其面积为$\frac{1}{2}r^2 = 3$,
解这个方程,我们得到$r^2 = 6$,
圆的面积公式为$\pi r^2$,将$r^2 = 6$代入,得到圆的面积为$6\pi$ $cm^2$。
答案:$6\pi$。
8. 一个圆柱的底面周长与高相等,如果高缩短2厘米,表面积减少12.56平方厘米,那么原来圆柱的体积是(
19.7192
)立方厘米。
答案:
解析:本题考查圆柱的侧面积和体积公式。
设圆柱的底面半径为$r$厘米。
已知底面周长与高相等,则高$h = 2\pi r$。
当高缩短$2$厘米时,表面积减少的部分就是高为$2$厘米的圆柱的侧面积。
圆柱的侧面积公式为$S = 2\pi rh$(其中$r$为底面半径,$h$为高),则:
$2\pi r× 2 = 12.56$
$4\pi r = 12.56$
$r = 12.56÷ 4÷ \pi$
$r = 1$
因为底面周长与高相等,底面周长$C = 2\pi r = 2× 3.14× 1 = 6.28$(厘米),所以高$h = 6.28$厘米。
圆柱的体积公式为$V = \pi r^{2}h$,则:
$V = 3.14× 1^{2}× 6.28 = 19.7192$(立方厘米)
答案: 19.7192。
设圆柱的底面半径为$r$厘米。
已知底面周长与高相等,则高$h = 2\pi r$。
当高缩短$2$厘米时,表面积减少的部分就是高为$2$厘米的圆柱的侧面积。
圆柱的侧面积公式为$S = 2\pi rh$(其中$r$为底面半径,$h$为高),则:
$2\pi r× 2 = 12.56$
$4\pi r = 12.56$
$r = 12.56÷ 4÷ \pi$
$r = 1$
因为底面周长与高相等,底面周长$C = 2\pi r = 2× 3.14× 1 = 6.28$(厘米),所以高$h = 6.28$厘米。
圆柱的体积公式为$V = \pi r^{2}h$,则:
$V = 3.14× 1^{2}× 6.28 = 19.7192$(立方厘米)
答案: 19.7192。
二、判断题。(对的打“√”,错的打“×”)(每小题2分,共10分)
1. 圆柱的体积比圆锥的体积多2倍。(
2. 任何一个梯形都可以分成两个等高的三角形。(
3. 一个正方形的周长扩大到原来的3倍,面积就扩大到原来的6倍。(
4. 梯形的面积是平行四边形面积的一半。(
5. 一个圆柱的底面周长和高相等,这个圆柱沿高展开的侧面展开图是正方形。(
1. 圆柱的体积比圆锥的体积多2倍。(
×
)2. 任何一个梯形都可以分成两个等高的三角形。(
√
)3. 一个正方形的周长扩大到原来的3倍,面积就扩大到原来的6倍。(
×
)4. 梯形的面积是平行四边形面积的一半。(
×
)5. 一个圆柱的底面周长和高相等,这个圆柱沿高展开的侧面展开图是正方形。(
√
)
答案:
解析:
1. 圆柱和圆锥的体积公式分别为$V_{cylinder} = \pi r^{2}h$和$V_{cone} = \frac{1}{3}\pi r^{2}h$。圆柱的体积是圆锥体积的3倍,而不是多2倍,所以此题错误。
2. 梯形有一组对边平行。从梯形的一个顶点作另一条对角线的平行线,可以将梯形分成两个等高的三角形。所以此题正确。
3. 正方形的周长扩大到原来的3倍,意味着边长也扩大到原来的3倍。面积会扩大到原来的$3^2 = 9$倍,而不是6倍。所以此题错误。
4. 梯形的面积公式为$S_{trapezoid} = \frac{(a+b)h}{2}$,平行四边形的面积公式为$S_{parallelogram} = ah$或$S = bh$。梯形的面积并不一定是平行四边形面积的一半,这取决于梯形和平行四边形的具体尺寸。所以此题错误。
5. 圆柱的侧面展开后是一个矩形,其中长是底面周长,宽是高。如果底面周长和高相等,那么展开后的侧面就是一个正方形。所以此题正确。
答案:
1. ×
2. √
3. ×
4. ×
5. √
1. 圆柱和圆锥的体积公式分别为$V_{cylinder} = \pi r^{2}h$和$V_{cone} = \frac{1}{3}\pi r^{2}h$。圆柱的体积是圆锥体积的3倍,而不是多2倍,所以此题错误。
2. 梯形有一组对边平行。从梯形的一个顶点作另一条对角线的平行线,可以将梯形分成两个等高的三角形。所以此题正确。
3. 正方形的周长扩大到原来的3倍,意味着边长也扩大到原来的3倍。面积会扩大到原来的$3^2 = 9$倍,而不是6倍。所以此题错误。
4. 梯形的面积公式为$S_{trapezoid} = \frac{(a+b)h}{2}$,平行四边形的面积公式为$S_{parallelogram} = ah$或$S = bh$。梯形的面积并不一定是平行四边形面积的一半,这取决于梯形和平行四边形的具体尺寸。所以此题错误。
5. 圆柱的侧面展开后是一个矩形,其中长是底面周长,宽是高。如果底面周长和高相等,那么展开后的侧面就是一个正方形。所以此题正确。
答案:
1. ×
2. √
3. ×
4. ×
5. √
1.(云南大理)用同样长的铁丝分别围成长方形、正方形、等边三角形和圆,那么面积最大的是(
A.长方形
B.正方形
C.等边三角形
D.圆
D
)。A.长方形
B.正方形
C.等边三角形
D.圆
答案:
假设铁丝长度为12厘米。
长方形:设长为4厘米,宽为(12÷2-4)=2厘米,面积=4×2=8平方厘米。
正方形:边长=12÷4=3厘米,面积=3×3=9平方厘米。
等边三角形:边长=12÷3=4厘米,高≈√(4²-2²)=√12≈3.464厘米,面积≈4×3.464÷2≈6.928平方厘米。
圆:半径=12÷(2×3.14)≈1.91厘米,面积≈3.14×1.91²≈11.46平方厘米。
11.46>9>8>6.928,面积最大的是圆。
D
长方形:设长为4厘米,宽为(12÷2-4)=2厘米,面积=4×2=8平方厘米。
正方形:边长=12÷4=3厘米,面积=3×3=9平方厘米。
等边三角形:边长=12÷3=4厘米,高≈√(4²-2²)=√12≈3.464厘米,面积≈4×3.464÷2≈6.928平方厘米。
圆:半径=12÷(2×3.14)≈1.91厘米,面积≈3.14×1.91²≈11.46平方厘米。
11.46>9>8>6.928,面积最大的是圆。
D
2. 六(1)班王小华的位置在(5,5),(
A.(5,6)
B.(6,5)
C.(5,4)
D.(6,6)
A
)是他正后桌的位置。A.(5,6)
B.(6,5)
C.(5,4)
D.(6,6)
答案:
解析:
本题考查的是用数对表示位置的知识。
在数对中,第一个数表示列,第二个数表示行。
已知王小华的位置是(5,5),这意味着王小华坐在第5列,第5行。
正后桌的位置,意味着列数不变,行数加1。
因此,王小华正后桌的位置应该是第5列,第6行,用数对表示就是(5,6)。
答案:A (5,6)。
本题考查的是用数对表示位置的知识。
在数对中,第一个数表示列,第二个数表示行。
已知王小华的位置是(5,5),这意味着王小华坐在第5列,第5行。
正后桌的位置,意味着列数不变,行数加1。
因此,王小华正后桌的位置应该是第5列,第6行,用数对表示就是(5,6)。
答案:A (5,6)。
3. 用两个长4 dm、宽2 dm、高3 dm的长方体拼成一个大长方体,这个大长方体的表面积最小是
A.88
B.56
C.80
D.48
80
dm²。A.88
B.56
C.80
D.48
答案:
一个长方体表面积:$(4×2+4×3+2×3)×2=52(dm^2)$
两个长方体表面积之和:$52×2=104(dm^2)$
三种拼接方式减少的面积:
1. 长×宽面拼接:$4×2×2=16(dm^2)$,大长方体表面积:$104-16=88(dm^2)$
2. 长×高面拼接:$4×3×2=24(dm^2)$,大长方体表面积:$104-24=80(dm^2)$
3. 宽×高面拼接:$2×3×2=12(dm^2)$,大长方体表面积:$104-12=92(dm^2)$
最小表面积是$80dm^2$。
C
两个长方体表面积之和:$52×2=104(dm^2)$
三种拼接方式减少的面积:
1. 长×宽面拼接:$4×2×2=16(dm^2)$,大长方体表面积:$104-16=88(dm^2)$
2. 长×高面拼接:$4×3×2=24(dm^2)$,大长方体表面积:$104-24=80(dm^2)$
3. 宽×高面拼接:$2×3×2=12(dm^2)$,大长方体表面积:$104-12=92(dm^2)$
最小表面积是$80dm^2$。
C
4. 将一个周长为6π cm的圆变换成面积为$36π cm^2$的圆,实际是按(
A.1∶3
B.2∶1
C.3∶1
D.4∶1
B
)的比放大的。A.1∶3
B.2∶1
C.3∶1
D.4∶1
答案:
原圆周长:$6\pi = 2\pi r_1$,得$r_1 = 3\ cm$。
新圆面积:$36\pi = \pi r_2^2$,得$r_2 = 6\ cm$。
半径比:$r_1:r_2 = 3:6 = 1:2$,放大比为$2:1$。
答案:B
新圆面积:$36\pi = \pi r_2^2$,得$r_2 = 6\ cm$。
半径比:$r_1:r_2 = 3:6 = 1:2$,放大比为$2:1$。
答案:B
5.(甘肃武威)边长是16厘米的正方形内有一个直径为10厘米的圆,如果这个圆在正方形内任意移动,那么正方形内不能被圆覆盖的面积是(
A.100-16π
B.256-25π
C.256-64π
D.100-25π
B
)平方厘米。
A.100-16π
B.256-25π
C.256-64π
D.100-25π
答案:
解析:本题考查正方形和圆的面积计算。
正方形的边长是$16$厘米,
所以正方形的面积是$16× 16=256$(平方厘米)。
圆的直径为$10$厘米,半径为$5$厘米,
所以圆的面积是$\pi × 5^2=25\pi$(平方厘米)。
正方形内不能被圆覆盖的面积等于正方形的面积减去圆的面积,即$256-25\pi$(平方厘米)。
答案:B.$256-25\pi$。
正方形的边长是$16$厘米,
所以正方形的面积是$16× 16=256$(平方厘米)。
圆的直径为$10$厘米,半径为$5$厘米,
所以圆的面积是$\pi × 5^2=25\pi$(平方厘米)。
正方形内不能被圆覆盖的面积等于正方形的面积减去圆的面积,即$256-25\pi$(平方厘米)。
答案:B.$256-25\pi$。
查看更多完整答案,请扫码查看


