《2025年名校优录小升初总复习六年级数学人教版》

1. 按要求分一分。
①
②

(1)在图形①中画一条线段,把它分割成一个直角三角形和一个平行四边形。
(2)在图形②中画一条线段,把它分割成一个三角形和一个梯形。

答案： 解析：本题可根据直角三角形、平行四边形、三角形和梯形的特征，结合所给图形的特点来进行分割。
(1) 对于图形①（直角梯形），要把它分割成一个直角三角形和一个平行四边形，可利用平行四边形对边平行的特征，从梯形右上角的顶点向底边作一条垂直于底边的线段，这样就把梯形分割成了一个直角三角形和一个平行四边形。
(2) 对于图形②（平行四边形），要把它分割成一个三角形和一个梯形，可从平行四边形的一个顶点向对边（非顶点）作一条线段，这样就把平行四边形分割成了一个三角形和一个梯形。
答案：
(1) 图略（从图形①右上角的顶点向底边作一条垂直于底边的线段）。
(2) 图略（从图形②的一个顶点向对边非顶点作一条线段）。

2. 过 P 点作 AB 的垂线和 CD 的平行线。

答案： 图略（过点$P$作$AB$的垂线，即过点$P$作与$AB$相交且夹角为$90^{\circ}$的直线；过点$P$作$CD$的平行线，即过点$P$作与$CD$不相交的直线 ）。

3. 如图,从 A、B 两村各挖一条水渠与河相通,在 B 村的东边修一个圆形游泳池。
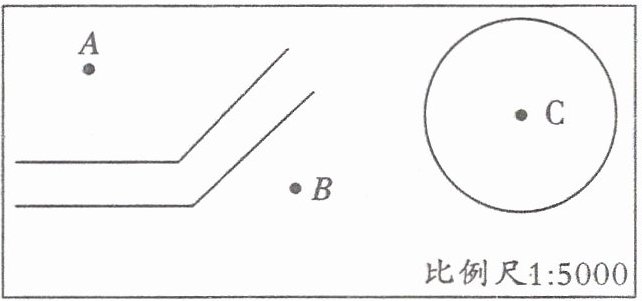
(1)要使水渠最短,应怎样挖？请在图中画出来。
(2)如果以点 C 为圆心修一个直径是 100 m 的圆形游泳池,请你在图中画出来。(先算出半径)

答案：
(1)解析：从直线外一点到这条直线所作的垂线段最短。
答案：从$B$村向河边作垂线，这条垂线就是使水渠最短的挖法，图略。
(2)解析：已知圆的直径是$100m$，根据半径等于直径的一半，可求出半径为$100÷2 = 50m$。再根据比例尺$1:5000$，将半径的实际长度换算为图上距离，$50m = 5000cm$，$5000÷5000 = 1cm$，即图上半径为$1cm$。
答案：半径$r = 100÷2 = 50(m)$，以点$C$为圆心，画半径为$1cm$（图上距离）的圆，图略。

1.

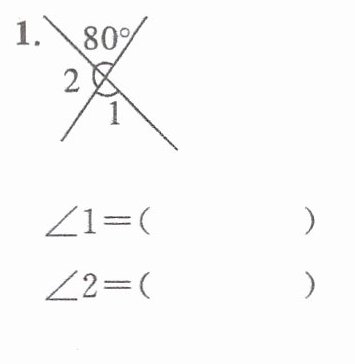
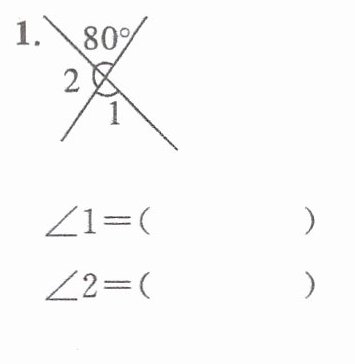
∠1=80°
∠2=100°

答案： ∠1=80°
∠2=100°

2.
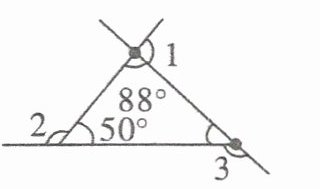
∠1= ( )
∠2= ( )
∠3= ( )

答案： 1. 首先求$\angle1$：
根据平角的定义，平角$ = 180^{\circ}$，$\angle1$与$88^{\circ}$角组成平角。
所以$\angle1=180^{\circ}-88^{\circ}=92^{\circ}$。
2. 然后求$\angle2$：
根据平角的定义，$\angle2$与$50^{\circ}$角组成平角。
所以$\angle2 = 180^{\circ}-50^{\circ}=130^{\circ}$。
3. 最后求$\angle3$：
先根据三角形内角和定理，三角形内角和$S = 180^{\circ}$，设三角形第三个内角为$\angle A$，则$\angle A=180^{\circ}-88^{\circ}-50^{\circ}=42^{\circ}$。
又因为$\angle3$与$\angle A$组成平角，根据平角定义。
所以$\angle3=180^{\circ}-42^{\circ}=138^{\circ}$。
故答案依次为：$92^{\circ}$；$130^{\circ}$；$138^{\circ}$。

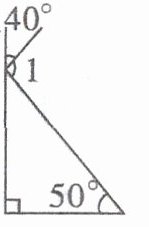
3.
∠1= ( )

答案： ∠1=180°-40°-40°=100°

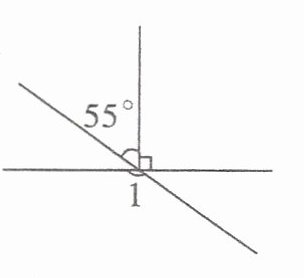
4.
∠1= ( )

答案： 180°-90°-55°=35°
∠1=180°-35°=145°

1. 小明的红领巾是一个近似的等腰三角形,其中一个角是 120°,其余两个角各是多少度？

答案： 解析：
本题考查等腰三角形的性质和三角形内角和定理。
等腰三角形有两个相等的角，这两个角对应的边也是相等的。
三角形三个内角的和总是180°。
已知等腰三角形其中一个角是120°，需要找出其余两个角的度数。
首先，三角形的三个内角之和为180°，所以其余两个角的度数之和为：
$180° - 120° = 60°$
由于这是一个等腰三角形，所以其余两个角是相等的。
每个角的度数为：
$60° ÷ 2 = 30°$
答案：
其余两个角各是30°。

2. 如图,李大爷沿墙用篱笆围了一个等腰梯形的养鸡场。已知梯形的腰长为 6 米,篱笆共长 27 米。则这个等腰梯形的上、下底之和是多少米？

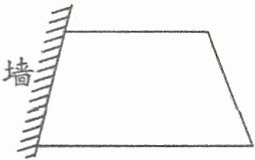
答案： 解析：本题考查了等腰梯形的周长计算知识点。题目中给出等腰梯形的腰长以及篱笆的总长度，因为等腰梯形两腰长度相等，所以用篱笆的总长度减去两条腰的长度，即可得到上、下底之和。
答案：因为等腰梯形的两腰长相等，已知梯形的腰长为$6$米，所以两条腰的长度为$6×2 = 12$（米）。
又因为篱笆共长$27$米，即等腰梯形的上底、下底与两腰的长度之和为$27$米，那么上、下底之和是$27 - 12 = 15$（米）。
答：这个等腰梯形的上、下底之和是$15$米。

3.(四川广安)王老师准备用一根 40 厘米长的铁丝围成一个等腰三角形,如果有一条边长 10 厘米,那么另外两边应该是多少厘米？

答案： 解析：
本题考查等腰三角形的性质以及三角形的三边关系。
分情况考虑：
如果10厘米长的边为底边，那么腰的长度为$(40 - 10) ÷ 2 = 15$（厘米）。
根据三角形的三边关系，任意两边之和大于第三边，$10 + 15 \gt 15$，$15 + 15 \gt 10$，满足条件。
如果10厘米长的边为腰，那么底边的长度为$40 - 10 × 2 = 20$（厘米）。
此时$10 + 10 = 20$，不满足三角形的三边关系。
答案：
另外两边应该是15厘米，15厘米。

4.(云南玉溪)如下图是一张长方形纸折起来以后的图形。已知∠1= 30°,则∠2 的度数是多少？

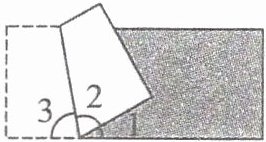
答案： ∠2=(180°-∠1)÷2=(180°-30°)÷2=75°
答：∠2的度数是75°。