2025年名校优录小升初总复习六年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年名校优录小升初总复习六年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
3.下面的数中,一个零也不读的是(
A.808008
B.808800
C.808080
D.880800
B
)。A.808008
B.808800
C.808080
D.880800
答案:
解析:本题可根据整数的读法来逐一分析选项,判断哪个数一个零也不读。
整数的读法为:从高位到低位,一级一级地读,每一级末尾的$0$都不读出来,其它数位连续几个$0$都只读一个零。
选项A:$808008$
读作:八十万八千零八,读$1$个零,不符合“一个零也不读”的要求。
选项B:$808800$
读作:八十万八千八百,一个零也不读,符合要求。
选项C:$808080$
读作:八十万八千零八十,读$1$个零,不符合“一个零也不读”的要求。
选项D:$880800$
读作:八十八万零八百,读$1$个零,不符合“一个零也不读”的要求。
答案:B。
整数的读法为:从高位到低位,一级一级地读,每一级末尾的$0$都不读出来,其它数位连续几个$0$都只读一个零。
选项A:$808008$
读作:八十万八千零八,读$1$个零,不符合“一个零也不读”的要求。
选项B:$808800$
读作:八十万八千八百,一个零也不读,符合要求。
选项C:$808080$
读作:八十万八千零八十,读$1$个零,不符合“一个零也不读”的要求。
选项D:$880800$
读作:八十八万零八百,读$1$个零,不符合“一个零也不读”的要求。
答案:B。
4.(山西晋中)一个数“四舍五入”到万位的近似数是28万,这个数不可能是(
A.281792
B.277639
C.280001
D.273846
D
)。A.281792
B.277639
C.280001
D.273846
答案:
解析:本题考查“四舍五入”法取近似值的知识点。需要判断每个选项“四舍五入”到万位后是否为$28$万。
A选项,$281792$,千位是$1$,小于$5$,舍去,所以$281792\approx28$万。
B选项,$277639$,千位是$7$,大于$5$,进一,所以$277639\approx28$万。
C选项,$280001$,千位是$0$,小于$5$,舍去,所以$280001\approx28$万。
D选项,$273846$,千位是$3$,小于$5$,舍去,所以$273846\approx27$万。
答案:D。
A选项,$281792$,千位是$1$,小于$5$,舍去,所以$281792\approx28$万。
B选项,$277639$,千位是$7$,大于$5$,进一,所以$277639\approx28$万。
C选项,$280001$,千位是$0$,小于$5$,舍去,所以$280001\approx28$万。
D选项,$273846$,千位是$3$,小于$5$,舍去,所以$273846\approx27$万。
答案:D。
5.若79□996≈80万(“四舍五入”取近似值),那么,□里可以填的数字个数是(
A.5个
B.4个
C.2个
D.3个
A
)。A.5个
B.4个
C.2个
D.3个
答案:
解析:本题考查“四舍五入”取近似值的应用。
“四舍五入”是一种常用的取近似值的方法,其规则是:观察需要保留的下一位数字,如果该数字小于5,则舍去;如果该数字大于等于5,则进位。
题目中给出的数是79□996,需要取到万位的近似值,且近似值为80万。
观察万位的下一位,即千位上的数字,由于题目中千位是□,是一个未知数,需要根据“四舍五入”的规则来判断。
由于近似值为80万,说明万位上的数字9进行了进位,那么千位上的数字□必须大于等于5,才能使得万位上的9进位。
因此,千位上的数字□可以取的值有:5,6,7,8,9。共5个值。
答案:A
“四舍五入”是一种常用的取近似值的方法,其规则是:观察需要保留的下一位数字,如果该数字小于5,则舍去;如果该数字大于等于5,则进位。
题目中给出的数是79□996,需要取到万位的近似值,且近似值为80万。
观察万位的下一位,即千位上的数字,由于题目中千位是□,是一个未知数,需要根据“四舍五入”的规则来判断。
由于近似值为80万,说明万位上的数字9进行了进位,那么千位上的数字□必须大于等于5,才能使得万位上的9进位。
因此,千位上的数字□可以取的值有:5,6,7,8,9。共5个值。
答案:A
6.(山东临沂)一个两位数,它十位上的数字是8,十位上的数字比个位上的数字的2倍多2,这个两位数是(
A.85
B.58
C.83
D.38
C
)。A.85
B.58
C.83
D.38
答案:
解析:题目考查两位数的构造以及数字之间关系的计算。
设这个两位数个位上的数字为$x$。
根据题目条件“十位上的数字比个位上的数字的2倍多2”,可以列出方程:
$2x + 2 = 8$,
解这个方程,得到:
$2x = 6$,
$x = 3$。
因此,这个两位数的个位数字是3,十位数字是8,所以这个两位数是83。
答案:C。
设这个两位数个位上的数字为$x$。
根据题目条件“十位上的数字比个位上的数字的2倍多2”,可以列出方程:
$2x + 2 = 8$,
解这个方程,得到:
$2x = 6$,
$x = 3$。
因此,这个两位数的个位数字是3,十位数字是8,所以这个两位数是83。
答案:C。
7.趣味数学游戏:把两个多位数用两个同样大小的纸板挡住,只露出最高位上的数字(如下图),则两个数相比,(

A.甲数大
B.乙数大
C.一样大
D.无法确定
D
)。
A.甲数大
B.乙数大
C.一样大
D.无法确定
答案:
解析:本题只给出了甲、乙两个数的最高位数字,甲数最高位是5,乙数最高位是4,但不知道这两个数的位数以及除最高位外其他数位上的数字情况。例如甲数可能是50,乙数可能是499,此时乙数大;甲数也可能是5000,乙数是40,此时甲数大。所以仅根据所给信息无法确定两个数的大小。
答案:D。
答案:D。
8.科学研究表明,海拔每增加1千米,气温约下降6℃,从右图中判断出点A处的气温约是(
A.-3℃
B.3℃
C.24℃
D.18℃
A
)。A.-3℃
B.3℃
C.24℃
D.18℃
答案:
本题可先根据已知条件算出点$A$与点$B$的海拔差,再结合海拔每增加$1$千米气温约下降$6℃$,计算出点$A$比点$B$的气温低多少,最后用点$B$的气温减去点$A$比点$B$低的气温,即可得到点$A$处的气温。
步骤一:计算点$A$与点$B$的海拔差
已知点$A$的海拔是$5000$米,点$B$的海拔是$1000$米,那么点$A$与点$B$的海拔差为:
$5000 - 1000 = 4000$(米)
因为$1$千米$ = 1000$米,所以$4000$米$ = 4000÷1000 = 4$千米。
步骤二:计算点$A$比点$B$的气温低多少
已知海拔每增加$1$千米,气温约下降$6℃$,点$A$与点$B$的海拔差是$4$千米,那么点$A$比点$B$的气温低:
$4×6 = 24$(℃)
步骤三:计算点$A$处的气温
已知点$B$处的气温是$21℃$,点$A$比点$B$的气温低$24℃$,那么点$A$处的气温为:
$21 - 24 = -3$(℃)
综上,点$A$处的气温约是$-3℃$,答案选A。
步骤一:计算点$A$与点$B$的海拔差
已知点$A$的海拔是$5000$米,点$B$的海拔是$1000$米,那么点$A$与点$B$的海拔差为:
$5000 - 1000 = 4000$(米)
因为$1$千米$ = 1000$米,所以$4000$米$ = 4000÷1000 = 4$千米。
步骤二:计算点$A$比点$B$的气温低多少
已知海拔每增加$1$千米,气温约下降$6℃$,点$A$与点$B$的海拔差是$4$千米,那么点$A$比点$B$的气温低:
$4×6 = 24$(℃)
步骤三:计算点$A$处的气温
已知点$B$处的气温是$21℃$,点$A$比点$B$的气温低$24℃$,那么点$A$处的气温为:
$21 - 24 = -3$(℃)
综上,点$A$处的气温约是$-3℃$,答案选A。
四、在直线上用点表示下面各数。
-3、+2、$-\frac{1}{2}$、2.5、3
-3、+2、$-\frac{1}{2}$、2.5、3
答案:
解析:本题考查在直线上表示数。
在直线上,以0为界,规定了0的右边为正,左边为负。
-3在0的左边,距离0点3个单位长度;
+2在0的右边,距离0点2个单位长度;
$-\frac{1}{2}$在0的左边,距离0点$\frac{1}{2}$个单位长度;
2.5在0的右边,距离0点2.5个单位长度;
3在0的右边,距离0点3个单位长度。
图略。
在直线上,以0为界,规定了0的右边为正,左边为负。
-3在0的左边,距离0点3个单位长度;
+2在0的右边,距离0点2个单位长度;
$-\frac{1}{2}$在0的左边,距离0点$\frac{1}{2}$个单位长度;
2.5在0的右边,距离0点2.5个单位长度;
3在0的右边,距离0点3个单位长度。
图略。
五、用8,3,7,0,0,0组成一个六位数。(每题写一个即可)
1.只读一个零的数:______
2.读两个零的数:______
3.一个零都不读的数:______
4.与700000最接近的数:______
5.万位上的数字是0的最大六位数:______
1.只读一个零的数:______
2.读两个零的数:______
3.一个零都不读的数:______
4.与700000最接近的数:______
5.万位上的数字是0的最大六位数:______
答案:
800370
800307
837000
700038
807300
800307
837000
700038
807300
1.(青海玉树)某车间5名工人一共加工零件个数情况如下表,以300个为标准,超过的个数用正数表示,不足的个数用负数表示。
| 工人编号 | ① | ② | ③ | ④ | ⑤ |
| 个数/个 | +46 | -18 | -9 | +19 | +27 |

(1)(
(2)这5名工人一天一共加工零件多少个?平均每人加工零件多少?
| 工人编号 | ① | ② | ③ | ④ | ⑤ |
| 个数/个 | +46 | -18 | -9 | +19 | +27 |

(1)(
①
)号工人一天加工的零件最多,是(346
)个;(②
)号工人一天加工的零件最少,是(282
)个;最多和最少相差(64
)个。(2)这5名工人一天一共加工零件多少个?平均每人加工零件多少?
(2)一共加工1565个,平均每人加工313个。
答案:
解析:本题可根据正负数的意义求出每个工人实际加工零件的个数,再据此进行后续计算。
(1)
分析:
已知以$300$个为标准,超过的个数用正数表示,不足的个数用负数表示。
分别计算每个工人实际加工零件的个数:
工人①:$300 + 46 = 346$(个);
工人②:$300 - 18 = 282$(个);
工人③:$300 - 9 = 291$(个);
工人④:$300 + 19 = 319$(个);
工人⑤:$300 + 27 = 327$(个)。
比较$346$、$282$、$291$、$319$、$327$的大小,可得$346\gt327\gt319\gt291\gt282$。
所以①号工人一天加工的零件最多,是$346$个;②号工人一天加工的零件最少,是$282$个。
最多和最少相差:$346 - 282 = 64$(个)。
答案:
(1)①;$346$;②;$282$;$64$。
(2)
分析:
先求出$5$名工人超过或不足标准的零件总数,再加上$5$个$300$,即可得到$5$名工人一天一共加工零件的个数。
$5$名工人超过或不足标准的零件总数为:
$( + 46)+( - 18)+( - 9)+( + 19)+( + 27)$
$=46 - 18 - 9 + 19 + 27$
$=28 - 9 + 19 + 27$
$=19 + 19 + 27$
$=38 + 27$
$= 65$(个)
$5$个$300$是$5×300 = 1500$(个)。
那么$5$名工人一天一共加工零件:$1500 + 65 = 1565$(个)。
平均每人加工零件:$1565÷5 = 313$(个)。
答案:
(2)一共加工$1565$个,平均每人加工$313$个。
(1)
分析:
已知以$300$个为标准,超过的个数用正数表示,不足的个数用负数表示。
分别计算每个工人实际加工零件的个数:
工人①:$300 + 46 = 346$(个);
工人②:$300 - 18 = 282$(个);
工人③:$300 - 9 = 291$(个);
工人④:$300 + 19 = 319$(个);
工人⑤:$300 + 27 = 327$(个)。
比较$346$、$282$、$291$、$319$、$327$的大小,可得$346\gt327\gt319\gt291\gt282$。
所以①号工人一天加工的零件最多,是$346$个;②号工人一天加工的零件最少,是$282$个。
最多和最少相差:$346 - 282 = 64$(个)。
答案:
(1)①;$346$;②;$282$;$64$。
(2)
分析:
先求出$5$名工人超过或不足标准的零件总数,再加上$5$个$300$,即可得到$5$名工人一天一共加工零件的个数。
$5$名工人超过或不足标准的零件总数为:
$( + 46)+( - 18)+( - 9)+( + 19)+( + 27)$
$=46 - 18 - 9 + 19 + 27$
$=28 - 9 + 19 + 27$
$=19 + 19 + 27$
$=38 + 27$
$= 65$(个)
$5$个$300$是$5×300 = 1500$(个)。
那么$5$名工人一天一共加工零件:$1500 + 65 = 1565$(个)。
平均每人加工零件:$1565÷5 = 313$(个)。
答案:
(2)一共加工$1565$个,平均每人加工$313$个。
2.(河北唐山)学校、书店、小红家和小明家在同一条直线上,向东走为正,向西走为负。
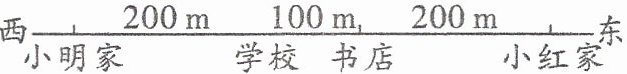
(1)如果小明从家走到书店,则应向(
(2)如果小红从家走了-200m,又走了-100m,则小红先后去了(
(3)如果小明从家出发走了+500m,又走了-300m,他现在的位置在哪里?请在上面的直线上用点A表示出来。
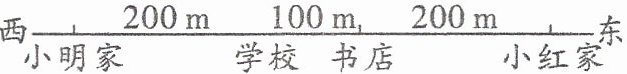
(1)如果小明从家走到书店,则应向(
东
)走(300
)m,可以表示为(+300m
)。(2)如果小红从家走了-200m,又走了-100m,则小红先后去了(
学校
)和(书店
)。(3)如果小明从家出发走了+500m,又走了-300m,他现在的位置在哪里?请在上面的直线上用点A表示出来。
图略(在书店位置标点A)。
答案:
解析:本题主要考查正负数的意义和应用以及在数轴上的位置表示。
(1)从图中可以看出小明家在书店西边$200+100 = 300m$处,所以小明从家走到书店,应向东走$300m$,根据向东走为正,可以表示为$+300m$。
(2)已知向东走为正,向西走为负,小红从家走了$-200m$,说明向西走了$200m$,到达学校位置;又走了$-100m$,即再向西走了$100m$,从学校向西走$100m$就到达书店,所以小红先后去了学校和书店。
(3)小明从家出发走了$+500m$,又走了$-300m$,$+500m$表示向东走$500m$,$-300m$表示向西走$300m$,那么小明实际向东走了$500 - 300 = 200m$,小明家向东$200m$处正好是书店,所以在直线上书店的位置标点A即可。
答案:
(1)东;$300$;$+300m$
(2)学校;书店
(3)图略(在书店位置标点A)。
(1)从图中可以看出小明家在书店西边$200+100 = 300m$处,所以小明从家走到书店,应向东走$300m$,根据向东走为正,可以表示为$+300m$。
(2)已知向东走为正,向西走为负,小红从家走了$-200m$,说明向西走了$200m$,到达学校位置;又走了$-100m$,即再向西走了$100m$,从学校向西走$100m$就到达书店,所以小红先后去了学校和书店。
(3)小明从家出发走了$+500m$,又走了$-300m$,$+500m$表示向东走$500m$,$-300m$表示向西走$300m$,那么小明实际向东走了$500 - 300 = 200m$,小明家向东$200m$处正好是书店,所以在直线上书店的位置标点A即可。
答案:
(1)东;$300$;$+300m$
(2)学校;书店
(3)图略(在书店位置标点A)。
查看更多完整答案,请扫码查看


