2025年名校优录小升初总复习六年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年名校优录小升初总复习六年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 通过纸上一点,能画(
无数
)条直线。通过纸上两点,能画(一
)条直线。
答案:
解析:本题可根据直线的性质来分别确定通过纸上一点和两点能画直线的条数。
通过纸上一点画直线的情况:
根据直线的性质,经过一点可以向不同方向画出无数条直线,所以通过纸上一点,能画无数条直线。
通过纸上两点画直线的情况:
两点确定一条直线,即通过纸上两点,只能画一条直线。
答案:无数;一
通过纸上一点画直线的情况:
根据直线的性质,经过一点可以向不同方向画出无数条直线,所以通过纸上一点,能画无数条直线。
通过纸上两点画直线的情况:
两点确定一条直线,即通过纸上两点,只能画一条直线。
答案:无数;一
2. 下图中有(

3
)条线段,(6
)条射线,(1
)条直线。
答案:
解析:本题可根据线段、射线、直线的定义和特点来确定图中它们的数量。
线段的定义和数量:
线段是指直线上两点间的有限部分,有两个端点。
在图中,以$A$、$B$、$C$为端点组成的线段有:线段$AB$、线段$AC$、线段$BC$,共$3$条。
射线的定义和数量:
射线是指由线段的一端无限延长所形成的直的线,有一个端点。
图中每个点都可以向左右两个方向分别引出一条射线,$A$、$B$、$C$三个点,每个点引出$2$条射线,所以射线的总数为$3×2 = 6$条。
直线的定义和数量:
直线由无数个点构成,没有端点,向两端无限延长,长度无法度量。
图中只有$1$条直线,即直线$AC$(或直线$ABC$ )。
答案:$3$;$6$;$1$
线段的定义和数量:
线段是指直线上两点间的有限部分,有两个端点。
在图中,以$A$、$B$、$C$为端点组成的线段有:线段$AB$、线段$AC$、线段$BC$,共$3$条。
射线的定义和数量:
射线是指由线段的一端无限延长所形成的直的线,有一个端点。
图中每个点都可以向左右两个方向分别引出一条射线,$A$、$B$、$C$三个点,每个点引出$2$条射线,所以射线的总数为$3×2 = 6$条。
直线的定义和数量:
直线由无数个点构成,没有端点,向两端无限延长,长度无法度量。
图中只有$1$条直线,即直线$AC$(或直线$ABC$ )。
答案:$3$;$6$;$1$
3. 两条平行线之间的距离处处
相等
;从直线外一点到这条直线所画的线段中,垂线段
最短。
答案:
解析:本题考查平行线之间距离的性质以及点到直线距离的性质。
两条平行线之间的距离是指由一条平行线上的任意一点向另一条平行线作垂线的长度,由于平行线的性质,这个长度处处相等。
从直线外一点到这条直线可以画许多线段,但其中垂线段是最短的。
答案:相等;垂线段。
两条平行线之间的距离是指由一条平行线上的任意一点向另一条平行线作垂线的长度,由于平行线的性质,这个长度处处相等。
从直线外一点到这条直线可以画许多线段,但其中垂线段是最短的。
答案:相等;垂线段。
4. 3 时整,时针和分针组成的角的度数是(
90°
);6 时整,时针和分针组成的角的度数是(180°
)。
答案:
解析:本题考查时钟上时针和分针夹角的问题,需要知道时钟一圈为$360^{\circ}$,分针每小时转一圈,时针每$12$小时转一圈,通过计算时针和分针在不同时刻的位置来确定夹角的度数。
对于$3$时整:
时钟一圈为$360^{\circ}$,分针每小时转一圈,即$360^{\circ}$,时针每$12$小时转一圈,那么时针每小时转动的角度为$360÷12 = 30^{\circ}$。
$3$时整时,分针指向$12$,时针指向$3$,中间间隔了$3$个大格,每个大格的角度是$30^{\circ}$,所以夹角是$30×3 = 90^{\circ}$。
对于$6$时整:
$6$时整时,分针指向$12$,时针指向$6$,中间间隔了$6$个大格,每个大格$30^{\circ}$,所以夹角是$30×6 = 180^{\circ}$。
答案:$90^{\circ}$;$180^{\circ}$。
对于$3$时整:
时钟一圈为$360^{\circ}$,分针每小时转一圈,即$360^{\circ}$,时针每$12$小时转一圈,那么时针每小时转动的角度为$360÷12 = 30^{\circ}$。
$3$时整时,分针指向$12$,时针指向$3$,中间间隔了$3$个大格,每个大格的角度是$30^{\circ}$,所以夹角是$30×3 = 90^{\circ}$。
对于$6$时整:
$6$时整时,分针指向$12$,时针指向$6$,中间间隔了$6$个大格,每个大格$30^{\circ}$,所以夹角是$30×6 = 180^{\circ}$。
答案:$90^{\circ}$;$180^{\circ}$。
5. 用圆规画一个直径是 8 cm 的圆,圆规两脚间的距离是(
4
)厘米。
答案:
解析:圆规两脚间的距离是圆的半径。已知圆的直径为 8 cm,根据半径是直径的一半,可得半径$r = 8÷2 = 4$ cm,所以圆规两脚间的距离是 4 厘米。
答案:4
答案:4
6. 学校的伸缩铁门是应用了平行四边形具有
不稳定性
的特征,自行车三脚架运用了三角形的稳定性
特征。
答案:
解析:题目考查平行四边形和三角形的特性。平行四边形具有不稳定性,容易变形,所以学校的伸缩铁门可以灵活伸缩;三角形具有稳定性,自行车三脚架利用这一特性可以保持稳固。
答案:不稳定性;稳定性
答案:不稳定性;稳定性
7. 一个梯形的下底是上底的 3 倍,如果将上底延长 10 cm 就成了一个平行四边形,这个梯形的上底是(
5
)cm,下底是(15
)cm。
答案:
设梯形的上底为 $ x $ cm,则下底为 $ 3x $ cm。
因为上底延长 10 cm 后与下底相等(平行四边形对边相等),所以:
$ x + 10 = 3x $
$ 3x - x = 10 $
$ 2x = 10 $
$ x = 5 $
下底:$ 3x = 3×5 = 15 $
上底是 5 cm,下底是 15 cm。
5,15
因为上底延长 10 cm 后与下底相等(平行四边形对边相等),所以:
$ x + 10 = 3x $
$ 3x - x = 10 $
$ 2x = 10 $
$ x = 5 $
下底:$ 3x = 3×5 = 15 $
上底是 5 cm,下底是 15 cm。
5,15
8. 若一个三角形三个内角的度数比是 6:2:1,那么这个三角形是一个(
钝角
)三角形。
答案:
解析:三角形的内角和为$180^\circ$,已知度数比为6:2:1,因此可以通过设未知数的方式求解每个角的度数。设三个内角分别为$6x$,$2x$,$x$,则有$6x + 2x + x = 180^\circ$,解得$x = 20^\circ$。所以三个内角分别为$120^\circ$,$40^\circ$,$20^\circ$。其中有一个角大于$90^\circ$,所以这个三角形是钝角三角形。
答案:钝角
答案:钝角
二、判断题。(对的打“√”,错的打“×”)
1. 用 10 倍的放大镜看一个 10°的角,这个角就变成了 100°。(
2. 四个圆心角是 90°的扇形可以拼成一个圆。(
3. 长方形和正方形都是特殊的平行四边形。(
4. 一个角的两边越长,这个角就越大。(
5. 如果一个三角形中最小的角大于 45°,则这个三角形一定是锐角三角形。(
6. 两个完全一样的三角形只能拼成一个长方形。(
1. 用 10 倍的放大镜看一个 10°的角,这个角就变成了 100°。(
×
)2. 四个圆心角是 90°的扇形可以拼成一个圆。(
×
)3. 长方形和正方形都是特殊的平行四边形。(
√
)4. 一个角的两边越长,这个角就越大。(
×
)5. 如果一个三角形中最小的角大于 45°,则这个三角形一定是锐角三角形。(
√
)6. 两个完全一样的三角形只能拼成一个长方形。(
×
)
答案:
解析:
1. 题目考查的是对角度概念的理解。角度是由两条射线与其公共端点决定的,与图形的尺寸无关。因此,用放大镜看一个角,并不会改变其角度大小。所以该说法是错误的。
答案:×
2. 题目考查的是对圆和扇形的理解。四个圆心角是90°的扇形,如果它们的半径不相同,则无法拼成一个完整的圆。所以,仅仅知道扇形的圆心角是90°,并不能确定它们可以拼成一个圆。该说法是错误的。
答案:×
3. 题目考查的是对平行四边形、长方形和正方形的理解。长方形和正方形的对边都是平行的,满足平行四边形的定义,因此它们都是特殊的平行四边形。该说法是正确的。
答案:√
4. 题目考查的是对角度概念的理解。角的大小是由其夹角的度数决定的,与角的两边的长度无关。所以该说法是错误的。
答案:×
5. 题目考查的是对三角形的理解。如果一个三角形中最小的角都大于45°,那么该三角形的所有角都小于90°,因此它是一个锐角三角形。该说法是正确的。
答案:√
6. 题目考查的是对三角形的拼接的理解。两个完全一样的三角形可以拼成一个平行四边形,但不一定是长方形。只有当这两个三角形是直角三角形,并且它们的直角边相等时,才能拼成一个长方形。所以该说法是错误的。
答案:×
1. 题目考查的是对角度概念的理解。角度是由两条射线与其公共端点决定的,与图形的尺寸无关。因此,用放大镜看一个角,并不会改变其角度大小。所以该说法是错误的。
答案:×
2. 题目考查的是对圆和扇形的理解。四个圆心角是90°的扇形,如果它们的半径不相同,则无法拼成一个完整的圆。所以,仅仅知道扇形的圆心角是90°,并不能确定它们可以拼成一个圆。该说法是错误的。
答案:×
3. 题目考查的是对平行四边形、长方形和正方形的理解。长方形和正方形的对边都是平行的,满足平行四边形的定义,因此它们都是特殊的平行四边形。该说法是正确的。
答案:√
4. 题目考查的是对角度概念的理解。角的大小是由其夹角的度数决定的,与角的两边的长度无关。所以该说法是错误的。
答案:×
5. 题目考查的是对三角形的理解。如果一个三角形中最小的角都大于45°,那么该三角形的所有角都小于90°,因此它是一个锐角三角形。该说法是正确的。
答案:√
6. 题目考查的是对三角形的拼接的理解。两个完全一样的三角形可以拼成一个平行四边形,但不一定是长方形。只有当这两个三角形是直角三角形,并且它们的直角边相等时,才能拼成一个长方形。所以该说法是错误的。
答案:×
1.(江苏泰州)下列各选项中,分别用集合图表示出了我们在小学阶段学习过的一些平面图形之间的关系,其中表示正确的是(

C
)。
答案:
解析:本题考查小学阶段平面图形之间的包含与被包含关系。
选项A:梯形包含等腰梯形和直角梯形,等腰梯形和直角梯形是并列关系,不是包含关系,所以A选项错误。
选项B:四边形包含平行四边形和梯形,平行四边形包含长方形,长方形包含正方形,该选项图形关系错误,所以B选项错误。
选项C:三角形按角分类,可分为锐角三角形、钝角三角形和直角三角形,这三种三角形是并列关系,该选项图形关系正确,所以C选项正确。
选项D:三角形按边分类,可分为等腰三角形和不等边三角形,等边三角形是特殊的等腰三角形,不是并列关系,所以D选项错误。
答案:C。
选项A:梯形包含等腰梯形和直角梯形,等腰梯形和直角梯形是并列关系,不是包含关系,所以A选项错误。
选项B:四边形包含平行四边形和梯形,平行四边形包含长方形,长方形包含正方形,该选项图形关系错误,所以B选项错误。
选项C:三角形按角分类,可分为锐角三角形、钝角三角形和直角三角形,这三种三角形是并列关系,该选项图形关系正确,所以C选项正确。
选项D:三角形按边分类,可分为等腰三角形和不等边三角形,等边三角形是特殊的等腰三角形,不是并列关系,所以D选项错误。
答案:C。
2. 圆内的最长的线段是(
A.半径
B.直径
C.两个端点都在圆上的任意一条线段
D.经过圆心两端不在圆上的线段
B
)。A.半径
B.直径
C.两个端点都在圆上的任意一条线段
D.经过圆心两端不在圆上的线段
答案:
解析:本题考查平面图形的认识。
圆内最长的线段是经过圆心的线段,且两个端点都在圆上时,这条线段最长,也就是直径。
半径是圆心到圆上任意一点的线段,它不是最长的。
两个端点都在圆上的任意一条线段,不一定是直径,所以不一定是最长的。
经过圆心两端不在圆上的线段,不是圆内的线段。
答案:B。
圆内最长的线段是经过圆心的线段,且两个端点都在圆上时,这条线段最长,也就是直径。
半径是圆心到圆上任意一点的线段,它不是最长的。
两个端点都在圆上的任意一条线段,不一定是直径,所以不一定是最长的。
经过圆心两端不在圆上的线段,不是圆内的线段。
答案:B。
3. 一个梯形中最多有(
A.2
B.3
C.1
D.4
A
)个直角。A.2
B.3
C.1
D.4
答案:
解析:梯形是一组对边平行而另一组对边不平行的四边形。由于梯形有一组对边是平行的,当梯形中有直角时,通常是在平行边与不平行边的交点处形成。考虑到梯形中如果有一个直角,那么由于平行线的性质,与这个直角相邻的另一个角也必然是直角(同旁内角互补)。但梯形中不可能所有角都是直角,因为那样就构成了矩形或正方形,而不再是梯形。所以,梯形中最多只能有两个直角。
答案:A.2。
答案:A.2。
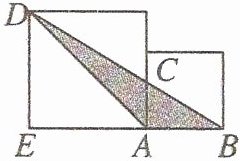
4. 如图,三角形 ABD 中 AB 边上的高是(
A.AC
B.DE
C.AD
D.BE
B
)。
A.AC
B.DE
C.AD
D.BE
答案:
解析:本题考查三角形高的定义。
三角形的高是指从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高。
在三角形$ABD$中,$AB$为底边,从$D$点向$AB$边所在直线作垂线,垂足为$E$,所以$DE$是$AB$边上的高。
答案:B。
三角形的高是指从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高。
在三角形$ABD$中,$AB$为底边,从$D$点向$AB$边所在直线作垂线,垂足为$E$,所以$DE$是$AB$边上的高。
答案:B。
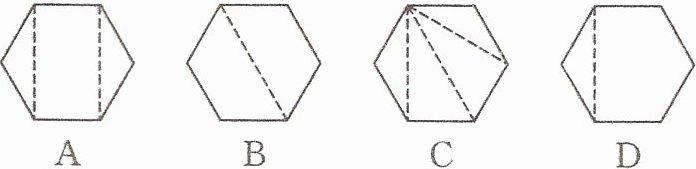
5.(广东广州)小伍在推算六边形的内角和时,把六边形分成若干个学过的图形来求内角和,然后列出算式:180°×2+360°,下面图(
C
)是与小伍所列算式相对应的分法。
答案:
解析:本题考查了三角形内角和与多边形内角和的关系。
小伍的算式$180^\circ × 2 + 360^\circ$可以这样理解:
$180^\circ × 2$表示两个三角形的内角和,
$360^\circ$表示一个四边形的内角和。
从算式看,六边形被分成了两个三角形和一个四边形。
A选项:六边形被分成了四个四边形,不符合算式。
B选项:六边形被分成了四个三角形,不符合算式。
C选项:六边形被分成了两个三角形和一个四边形,符合算式。
D选项:六边形被分成了两个四边形,不符合算式。
答案:C。
小伍的算式$180^\circ × 2 + 360^\circ$可以这样理解:
$180^\circ × 2$表示两个三角形的内角和,
$360^\circ$表示一个四边形的内角和。
从算式看,六边形被分成了两个三角形和一个四边形。
A选项:六边形被分成了四个四边形,不符合算式。
B选项:六边形被分成了四个三角形,不符合算式。
C选项:六边形被分成了两个三角形和一个四边形,符合算式。
D选项:六边形被分成了两个四边形,不符合算式。
答案:C。
6. 用一副三角尺不能画出(
A.120°
B.15°
C.125°
D.45°
C
)的角。A.120°
B.15°
C.125°
D.45°
答案:
解析:本题考查的是对三角尺角度的认识及应用。
首先,要知道一副常规的三角尺上主要有$30^\circ$、$45^\circ$、$60^\circ$和$90^\circ$这几种角度。
接下来,逐一分析每个选项:
A选项,$120^\circ$:这个角度可以由$90^\circ$和$30^\circ$两个角度相加得到,所以能画出。
B选项,$15^\circ$:这个角度可以由$45^\circ$和$30^\circ$两个角度相减得到(即$45^\circ - 30^\circ = 15^\circ$),或者由两个$30^\circ$的角的一半(即等腰直角三角形的一个锐角的一半再乘以2,但实际操作中就是$45^\circ-30^\circ$的差),所以也能画出。
C选项,$125^\circ$:尝试用三角尺上的所有角度进行加减组合,无法得到$125^\circ$,所以不能画出。
D选项,$45^\circ$:这个角度直接在三角尺上就有,所以能画出。
综上所述,不能画出的角度是$125^\circ$。
答案:C。
首先,要知道一副常规的三角尺上主要有$30^\circ$、$45^\circ$、$60^\circ$和$90^\circ$这几种角度。
接下来,逐一分析每个选项:
A选项,$120^\circ$:这个角度可以由$90^\circ$和$30^\circ$两个角度相加得到,所以能画出。
B选项,$15^\circ$:这个角度可以由$45^\circ$和$30^\circ$两个角度相减得到(即$45^\circ - 30^\circ = 15^\circ$),或者由两个$30^\circ$的角的一半(即等腰直角三角形的一个锐角的一半再乘以2,但实际操作中就是$45^\circ-30^\circ$的差),所以也能画出。
C选项,$125^\circ$:尝试用三角尺上的所有角度进行加减组合,无法得到$125^\circ$,所以不能画出。
D选项,$45^\circ$:这个角度直接在三角尺上就有,所以能画出。
综上所述,不能画出的角度是$125^\circ$。
答案:C。
7. 钟面上如果分针旋转半周,那么时针旋转的角度是(
A.15°
B.30°
C.60°
D.180°
A
)。A.15°
B.30°
C.60°
D.180°
答案:
分析:本题主要考查对钟面上时针和分针转动关系的理解以及角度的计算。
我们知道,钟面一圈是$360^\circ$,分针转一圈是$60$分钟,时针转一圈是$12$小时,$1$小时$ = 60$分钟,所以时针转一圈分针转$12$圈。
这意味着分针转得比时针快很多,当分针转动一定角度时,时针也会转动一定角度,且它们之间存在一定的比例关系。
选项A:
当分针旋转半周,也就是转了$180^\circ$。
因为分针转一圈($360^\circ$)是$60$分钟,那么转半周($180^\circ$)就是$30$分钟。
又因为时针转一圈($360^\circ$)是$12$小时,$12$小时换算成分钟是$12×60 = 720$分钟。
设时针在$30$分钟内旋转的角度为$x$,根据时针和分针旋转时间与角度的比例关系可得:
$\frac{x}{360^\circ}=\frac{30}{720}$
$x = 360^\circ×\frac{30}{720}= 15^\circ$,所以该选项正确。
选项B:
由上述计算可知,分针旋转半周时,时针旋转$15^\circ$,不是$30^\circ$,所以该选项错误。
选项C:
同理,时针旋转角度不是$60^\circ$,所以该选项错误。
选项D:
分针旋转半周是$180^\circ$,但时针旋转角度不是$180^\circ$,所以该选项错误。
答案:A。
我们知道,钟面一圈是$360^\circ$,分针转一圈是$60$分钟,时针转一圈是$12$小时,$1$小时$ = 60$分钟,所以时针转一圈分针转$12$圈。
这意味着分针转得比时针快很多,当分针转动一定角度时,时针也会转动一定角度,且它们之间存在一定的比例关系。
选项A:
当分针旋转半周,也就是转了$180^\circ$。
因为分针转一圈($360^\circ$)是$60$分钟,那么转半周($180^\circ$)就是$30$分钟。
又因为时针转一圈($360^\circ$)是$12$小时,$12$小时换算成分钟是$12×60 = 720$分钟。
设时针在$30$分钟内旋转的角度为$x$,根据时针和分针旋转时间与角度的比例关系可得:
$\frac{x}{360^\circ}=\frac{30}{720}$
$x = 360^\circ×\frac{30}{720}= 15^\circ$,所以该选项正确。
选项B:
由上述计算可知,分针旋转半周时,时针旋转$15^\circ$,不是$30^\circ$,所以该选项错误。
选项C:
同理,时针旋转角度不是$60^\circ$,所以该选项错误。
选项D:
分针旋转半周是$180^\circ$,但时针旋转角度不是$180^\circ$,所以该选项错误。
答案:A。
查看更多完整答案,请扫码查看


