2025年名校优录小升初总复习六年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年名校优录小升初总复习六年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1.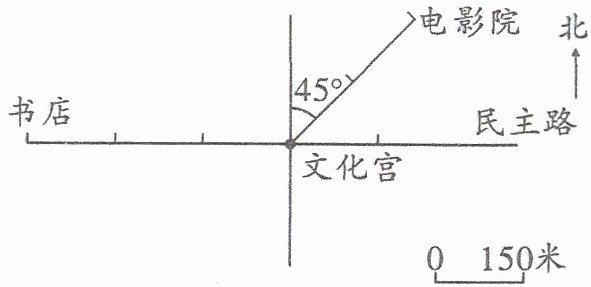
(1)如图,在文化宫东面300米处,有一条商业街与民主路互相垂直。在图上画直线表示出这条街,并标上“商业街”。(2分)
(2)电影院在文化宫(
(3)王冬以60米/分的速度从书店沿着民主路向东走,6分钟后他在文化宫(

(1)如图,在文化宫东面300米处,有一条商业街与民主路互相垂直。在图上画直线表示出这条街,并标上“商业街”。(2分)
(2)电影院在文化宫(
北
)偏(东
)(45
)°的方向上,距离是(300
)米。(4分)(3)王冬以60米/分的速度从书店沿着民主路向东走,6分钟后他在文化宫(
西
)面(180
)米处。(4分)
答案:
(1) (画图略:过文化宫东面2厘米处作民主路的垂线,并标“商业街”)
(2) 北;东;45;300
(3) 西;180
(1) (画图略:过文化宫东面2厘米处作民主路的垂线,并标“商业街”)
(2) 北;东;45;300
(3) 西;180
2.(1)将图形①绕点A(3,5)逆时针旋转90°,画出旋转后的图形,旋转后点B的位置用数对表示是(
(2)画一个与图形①面积相等的平行四边形。(2分)
(3)在图形②正南方向,按2∶1画出图形②放大后的图形,放大后的圆面积是原来圆面积的(
(5,6)
)。(4分)(2)画一个与图形①面积相等的平行四边形。(2分)
(3)在图形②正南方向,按2∶1画出图形②放大后的图形,放大后的圆面积是原来圆面积的(
4
)倍。(4分)
答案:
(1) 解析:本题考查旋转的知识点。解题方法是将图形①的各点绕点$A(3,5)$逆时针旋转$90^\circ$,然后确定旋转后点$B$的位置。
答案:$(5,6)$。
(2) 解析:本题考查平行四边形面积的知识点。解题方法是先计算图形①的面积,然后画一个面积相等的平行四边形。图形①是一个直角三角形,底为$2$格,高为$2$格,面积为:
$\frac{1}{2} × 2 × 2 = 2$。
可以画一个底为$2$格,高为$1$格的平行四边形,其面积也为$2$。
答案:图略。
(3) 解析:本题考查图形的放大与缩小以及圆的面积公式。解题方法是根据图形放大与缩小的意义,以图形②圆心为定点,按$2:1$的比放大图形②,再根据圆的面积公式$S = \pi r^2$求出放大前后的面积,进而求出放大后的圆面积是原来圆面积的几倍。
答案:$4$。
(1) 解析:本题考查旋转的知识点。解题方法是将图形①的各点绕点$A(3,5)$逆时针旋转$90^\circ$,然后确定旋转后点$B$的位置。
答案:$(5,6)$。
(2) 解析:本题考查平行四边形面积的知识点。解题方法是先计算图形①的面积,然后画一个面积相等的平行四边形。图形①是一个直角三角形,底为$2$格,高为$2$格,面积为:
$\frac{1}{2} × 2 × 2 = 2$。
可以画一个底为$2$格,高为$1$格的平行四边形,其面积也为$2$。
答案:图略。
(3) 解析:本题考查图形的放大与缩小以及圆的面积公式。解题方法是根据图形放大与缩小的意义,以图形②圆心为定点,按$2:1$的比放大图形②,再根据圆的面积公式$S = \pi r^2$求出放大前后的面积,进而求出放大后的圆面积是原来圆面积的几倍。
答案:$4$。
1. 玲玲过生日时,爸爸买来一个生日蛋糕。(如图)
(1)蛋糕盒的体积是多少立方厘米?(5分)
(2)扎这个蛋糕盒要多少厘米长的彩带?(打结处的彩带长20厘米)(5分)

(1)蛋糕盒的体积是多少立方厘米?(5分)
(2)扎这个蛋糕盒要多少厘米长的彩带?(打结处的彩带长20厘米)(5分)
答案:
解析:本题可根据圆柱的体积公式以及彩带长度的计算方法来分别求解两个问题。
(1)求蛋糕盒的体积:
蛋糕盒为圆柱体,圆柱体的体积公式为$V = \pi r^2h$(其中$V$是体积,$r$是底面半径,$h$是高,$\pi$通常取$3.14$)。
已知蛋糕盒底面直径为$40cm$,则半径$r = 40÷2 = 20cm$,高$h = 30cm$。
将$r = 20$、$h = 30$、$\pi = 3.14$代入体积公式可得:
$V=3.14×20^2×30$
$=3.14×400×30$
$=1256×30$
$= 37680$(立方厘米)
(2)求扎这个蛋糕盒所需彩带的长度:
观察图形可知,彩带的长度由$4$条蛋糕盒的高和$4$条底面直径以及打结处的长度组成。
已知蛋糕盒底面直径为$40cm$,高为$30cm$,打结处彩带长$20cm$。
则彩带长度为:
$4×30 + 4×40 + 20$
$=120 + 160 + 20$
$=280 + 20$
$= 300$(厘米)
答案:
(1)$3.14×(40÷2)^2×30 = 37680$(立方厘米)
答:蛋糕盒的体积是$37680$立方厘米。
(2)$4×30 + 4×40 + 20 = 300$(厘米)
答:扎这个蛋糕盒要$300$厘米长的彩带。
(1)求蛋糕盒的体积:
蛋糕盒为圆柱体,圆柱体的体积公式为$V = \pi r^2h$(其中$V$是体积,$r$是底面半径,$h$是高,$\pi$通常取$3.14$)。
已知蛋糕盒底面直径为$40cm$,则半径$r = 40÷2 = 20cm$,高$h = 30cm$。
将$r = 20$、$h = 30$、$\pi = 3.14$代入体积公式可得:
$V=3.14×20^2×30$
$=3.14×400×30$
$=1256×30$
$= 37680$(立方厘米)
(2)求扎这个蛋糕盒所需彩带的长度:
观察图形可知,彩带的长度由$4$条蛋糕盒的高和$4$条底面直径以及打结处的长度组成。
已知蛋糕盒底面直径为$40cm$,高为$30cm$,打结处彩带长$20cm$。
则彩带长度为:
$4×30 + 4×40 + 20$
$=120 + 160 + 20$
$=280 + 20$
$= 300$(厘米)
答案:
(1)$3.14×(40÷2)^2×30 = 37680$(立方厘米)
答:蛋糕盒的体积是$37680$立方厘米。
(2)$4×30 + 4×40 + 20 = 300$(厘米)
答:扎这个蛋糕盒要$300$厘米长的彩带。
2.(四川眉山)用铁皮制作圆柱形通风管,每节长60厘米,底面半径为5厘米,制作10节这样的通风管,至少需要多少平方米的铁皮?(6分)
答案:
一节通风管的侧面积:$2×3.14×5×60 = 1884$(平方厘米)
10节通风管的侧面积:$1884×10 = 18840$(平方厘米)
单位换算:$18840$平方厘米$=1.884$平方米
答:至少需要$1.884$平方米的铁皮。
10节通风管的侧面积:$1884×10 = 18840$(平方厘米)
单位换算:$18840$平方厘米$=1.884$平方米
答:至少需要$1.884$平方米的铁皮。
3.(湖南娄底)有一个圆锥形沙堆,底面周长是18.84米,高2.4米。把这些沙子均匀铺在一条长31.4米、宽3米的小路上,能铺多厚?(7分)
答案:
18.84÷3.14÷2=3(米)
3.14×3²×2.4×1/3=22.608(立方米)
22.608÷(31.4×3)=0.24(米)
答:能铺0.24米厚。
3.14×3²×2.4×1/3=22.608(立方米)
22.608÷(31.4×3)=0.24(米)
答:能铺0.24米厚。
4.(云南保山)图中整块长方形铁皮材料的长为16.56 m,如图剪裁的阴影部分正好做成一个圆柱体,求此圆柱体的体积。(7分)


答案:
设圆柱体的底面半径为$r$分米。
根据图形,长方形铁皮的长由圆柱体的底面周长和两条直径组成,即:
$2×3.14× r+2r=16.56$
$6.28r + 2r = 16.56$
$8.28r = 16.56$
$r = 2$
圆柱的高是两个底面直径,即:
$h = 2×2r = 2×2×2 = 8$(分米)
圆柱体的体积公式为:
$V = 3.14× r^2× h$
$V = 3.14×2^2×8$
$V = 3.14×4×8$
$V = 100.48$(立方分米)
综上所述:圆柱体的体积为100.48立方分米。
根据图形,长方形铁皮的长由圆柱体的底面周长和两条直径组成,即:
$2×3.14× r+2r=16.56$
$6.28r + 2r = 16.56$
$8.28r = 16.56$
$r = 2$
圆柱的高是两个底面直径,即:
$h = 2×2r = 2×2×2 = 8$(分米)
圆柱体的体积公式为:
$V = 3.14× r^2× h$
$V = 3.14×2^2×8$
$V = 3.14×4×8$
$V = 100.48$(立方分米)
综上所述:圆柱体的体积为100.48立方分米。
查看更多完整答案,请扫码查看


