2025年名校优录小升初总复习六年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年名校优录小升初总复习六年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1.要反映北京市一周气温的变化情况,最好选用(
折线
)统计图;要清楚地表示出六年级各班人数,最好选用(条形
)统计图;要清楚地表示出六年级各班人数占全年级总人数的百分比,最好选用(扇形
)统计图。
答案:
解析:
首先,我们分析每个问题的需求:
1. 要反映北京市一周气温的变化情况,需要选用能够展示时间变化趋势的统计图,这通常是折线统计图的特点。
2. 要清楚地表示出六年级各班人数,需要选用能够清晰展示每个项目(这里是各班)具体数量的统计图,这通常是条形统计图的特点。
3. 要清楚地表示出六年级各班人数占全年级总人数的百分比,需要选用能够展示各部分所占比例的统计图,这通常是扇形统计图的特点。
答案:
1. 折线
2. 条形
3. 扇形
首先,我们分析每个问题的需求:
1. 要反映北京市一周气温的变化情况,需要选用能够展示时间变化趋势的统计图,这通常是折线统计图的特点。
2. 要清楚地表示出六年级各班人数,需要选用能够清晰展示每个项目(这里是各班)具体数量的统计图,这通常是条形统计图的特点。
3. 要清楚地表示出六年级各班人数占全年级总人数的百分比,需要选用能够展示各部分所占比例的统计图,这通常是扇形统计图的特点。
答案:
1. 折线
2. 条形
3. 扇形
2.在一幅条形统计图中,如果用2 cm长的直条表示16吨,那么3 cm长的直条表示(
24
)吨。
答案:
解析:本题考查条形统计图中长度与数量之间的比例关系。
首先,我们需要找出长度与数量之间的比例关系。
题目中给出,2 cm长的直条表示16吨。那么,1 cm长的直条就表示 $\frac{16}{2} = 8(吨)$。
接着,我们可以用这个比例关系来找出3 cm长的直条表示的吨数。
3 cm长的直条表示的吨数就是 $3 × 8 = 24(吨)$。
答案:24吨。
首先,我们需要找出长度与数量之间的比例关系。
题目中给出,2 cm长的直条表示16吨。那么,1 cm长的直条就表示 $\frac{16}{2} = 8(吨)$。
接着,我们可以用这个比例关系来找出3 cm长的直条表示的吨数。
3 cm长的直条表示的吨数就是 $3 × 8 = 24(吨)$。
答案:24吨。
3.在期中考试中,优优语文、数学的平均分是92分,英语成绩是86分。她语文、数学、英语三门功课的平均成绩是(
90
)分。
答案:
解析:本题考查平均数的计算。
首先,我们知道优优语文和数学的平均分是92分。
平均分是所有分数加起来除以科目数,所以优优语文和数学的总分是:
$92 × 2 = 184(分)$
接着,我们知道优优的英语成绩是86分。
现在我们可以计算优优三门课的总分:
$184 + 86 = 270(分)$
最后,我们计算优优三门课的平均分:
$270 ÷ 3 = 90(分)$
答案:90分。
首先,我们知道优优语文和数学的平均分是92分。
平均分是所有分数加起来除以科目数,所以优优语文和数学的总分是:
$92 × 2 = 184(分)$
接着,我们知道优优的英语成绩是86分。
现在我们可以计算优优三门课的总分:
$184 + 86 = 270(分)$
最后,我们计算优优三门课的平均分:
$270 ÷ 3 = 90(分)$
答案:90分。
4.(贵州安顺)下图表示甲、乙、丙三个工人单独完成一项工程所需的天数。

(1)工作效率最高的工人是(
(2)甲、乙合作,完成全工程需(
(3)丙的工作效率是乙的(

(1)工作效率最高的工人是(
甲
)。(2)甲、乙合作,完成全工程需(
75/8
)天。(3)丙的工作效率是乙的(
125
)%。
答案:
(1)本题考查的是工作效率的计算。
将工作总量看作单位1。
根据工作效率=工作总量÷ 工作时间,可得:
甲的工作效率为1÷15=1/15;
乙的工作效率为1÷25=1/25;
丙的工作效率为1÷20=1/20。
由于1/15>1/20>1/25,
所以,甲的工作效率最高。
故答案为:甲。
(2)本题考查的是合作的工作时间。
甲、乙合作的工作效率为:1/15+1/25=8/75。
根据工作时间=工作总量÷工作效率,可得:
甲、乙合作完成全工程需要的时间为:1÷8/75=75/8(天)。
所以,甲、乙合作完成全工程需要75/8天。
(3)本题考查的是百分数的应用。
丙的工作效率是乙的:
(1/20) / (1/25) × 100% = 125%。
所以,丙的工作效率是乙的125%。
(1)本题考查的是工作效率的计算。
将工作总量看作单位1。
根据工作效率=工作总量÷ 工作时间,可得:
甲的工作效率为1÷15=1/15;
乙的工作效率为1÷25=1/25;
丙的工作效率为1÷20=1/20。
由于1/15>1/20>1/25,
所以,甲的工作效率最高。
故答案为:甲。
(2)本题考查的是合作的工作时间。
甲、乙合作的工作效率为:1/15+1/25=8/75。
根据工作时间=工作总量÷工作效率,可得:
甲、乙合作完成全工程需要的时间为:1÷8/75=75/8(天)。
所以,甲、乙合作完成全工程需要75/8天。
(3)本题考查的是百分数的应用。
丙的工作效率是乙的:
(1/20) / (1/25) × 100% = 125%。
所以,丙的工作效率是乙的125%。
5.小华骑车从家去相距5 km的图书馆借书,从下面的折线统计图可以看出:

(1)小华去图书馆的路上停车(
(2)从图书馆返回家时的速度是每分钟(

(1)小华去图书馆的路上停车(
20
)分钟,在图书馆借书用了(40
)分钟。(2)从图书馆返回家时的速度是每分钟(
0.25
)km。
答案:
(1)20,40
(2)0.25
(1)20,40
(2)0.25
二、判断题。(对的打“√”,错的打“×”)
1.条形统计图既可以竖着画,也可以横着画。(
2.折线统计图不但可以表示出数量的多少,而且能清楚地表示出数量增减变化情况。(
3.毛毛身高1.45米,他蹚过平均水深1.3米的小河,肯定没什么危险。(
4.一组数的平均数不会受偏大、偏小数的影响。(
5.有一辆客车从甲地开往乙地,2小时行了80千米,返回花了2.5小时,则往返的平均速度列式是(80÷2+80÷2.5)÷2。(
1.条形统计图既可以竖着画,也可以横着画。(
√
)2.折线统计图不但可以表示出数量的多少,而且能清楚地表示出数量增减变化情况。(
√
)3.毛毛身高1.45米,他蹚过平均水深1.3米的小河,肯定没什么危险。(
×
)4.一组数的平均数不会受偏大、偏小数的影响。(
×
)5.有一辆客车从甲地开往乙地,2小时行了80千米,返回花了2.5小时,则往返的平均速度列式是(80÷2+80÷2.5)÷2。(
×
)
答案:
解析:
1. 条形统计图的设计具有灵活性,可以根据需要选择竖式或横式展示,因此这个说法是正确的。
2. 折线统计图通过连接各数据点,能够直观地展示数据随时间或其他变量的变化趋势,因此这个说法是正确的。
3. 平均水深1.3米的小河,并不意味着河中所有地方的水深都是1.3米,可能某些地方的水深远超过1.45米,因此这个说法是错误的。
4. 平均数是所有数的和除以数的个数,因此会受到偏大或偏小数的影响,这个说法是错误的。
5. 平均速度的计算公式是总距离除以总时间,而不是简单地将去程和回程的平均速度相加后除以2,因此这个说法是错误的。
答案:
1. √
2. √
3. ×
4. ×
5. ×
1. 条形统计图的设计具有灵活性,可以根据需要选择竖式或横式展示,因此这个说法是正确的。
2. 折线统计图通过连接各数据点,能够直观地展示数据随时间或其他变量的变化趋势,因此这个说法是正确的。
3. 平均水深1.3米的小河,并不意味着河中所有地方的水深都是1.3米,可能某些地方的水深远超过1.45米,因此这个说法是错误的。
4. 平均数是所有数的和除以数的个数,因此会受到偏大或偏小数的影响,这个说法是错误的。
5. 平均速度的计算公式是总距离除以总时间,而不是简单地将去程和回程的平均速度相加后除以2,因此这个说法是错误的。
答案:
1. √
2. √
3. ×
4. ×
5. ×
1.(湖北武汉)为了清楚地比较武汉和成都两城市2024年月平均气温的变化情况,最好选用(
A.单式折线
B.复式折线
C.复式条形
D.扇形
B
)统计图。A.单式折线
B.复式折线
C.复式条形
D.扇形
答案:
解析:
本题考查的是统计图的认识及应用。
首先,需要明确题目中的需求:比较武汉和成都两城市2024年月平均气温的变化情况。这涉及到两个城市的气温数据,并且需要观察它们随时间(月份)的变化趋势。
接下来,分析各种统计图的特点:
单式折线统计图:用于展示一个数据系列随时间或其他变量的变化趋势。但本题需要比较两个城市的气温,所以单式折线统计图不适用。
复式折线统计图:可以同时展示两个或多个数据系列随时间或其他变量的变化趋势,便于比较它们之间的差异。这符合题目的需求。
复式条形统计图:用于展示不同类别数据的数量对比,但不适合展示时间序列数据的变化趋势。
扇形统计图:用于展示各部分在整体中的比例,与题目需求不符。
根据以上分析,为了清楚地比较武汉和成都两城市2024年月平均气温的变化情况,最好选用复式折线统计图。
答案:B。
本题考查的是统计图的认识及应用。
首先,需要明确题目中的需求:比较武汉和成都两城市2024年月平均气温的变化情况。这涉及到两个城市的气温数据,并且需要观察它们随时间(月份)的变化趋势。
接下来,分析各种统计图的特点:
单式折线统计图:用于展示一个数据系列随时间或其他变量的变化趋势。但本题需要比较两个城市的气温,所以单式折线统计图不适用。
复式折线统计图:可以同时展示两个或多个数据系列随时间或其他变量的变化趋势,便于比较它们之间的差异。这符合题目的需求。
复式条形统计图:用于展示不同类别数据的数量对比,但不适合展示时间序列数据的变化趋势。
扇形统计图:用于展示各部分在整体中的比例,与题目需求不符。
根据以上分析,为了清楚地比较武汉和成都两城市2024年月平均气温的变化情况,最好选用复式折线统计图。
答案:B。
2.兴隆商场今天1~5月空调销售情况如图,(

A.1~2月
B.2~3月
C.3~4月
D.4~5月
C
)增长幅度最大。
A.1~2月
B.2~3月
C.3~4月
D.4~5月
答案:
解析:本题考查对折线图的认识和分析。
从图中可以看出,1到2月销售量从0上升到200左右;2到3月从200上升到400左右;3到4月从400上升到800左右;4到5月从800上升到1000左右。
增长幅度最大的是3到4月。
答案:C。
从图中可以看出,1到2月销售量从0上升到200左右;2到3月从200上升到400左右;3到4月从400上升到800左右;4到5月从800上升到1000左右。
增长幅度最大的是3到4月。
答案:C。
3.一个调查数据被呈现在一扇形统计图里,下面条形图(
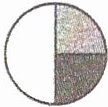

A.
B.
C.
D.
B
)与这个扇形图显示的是相同的数据。

A.
B.
C.
D.
答案:
解析:本题考查扇形统计图和条形统计图的特点,扇形统计图是用整个圆表示总数,用圆内各个扇形的大小表示各部分数量占总数的百分数,条形统计图是用一个单位长度表示一定的数量,根据数量的多少画成长短不同的直条,然后把这些直条按一定的顺序排列起来。
观察扇形统计图可知,灰色部分占比最大,白色部分次之,深灰色部分占比最小。
分析选项A:条形图中白色直条最高,灰色直条次之,深灰色直条最矮,不符合扇形统计图中各部分占比关系。
分析选项B:条形图中灰色直条最高,白色直条次之,深灰色直条最矮,符合扇形统计图中各部分占比关系。
分析选项C:条形图中白色直条最高,深灰色直条次之,灰色直条最矮,不符合扇形统计图中各部分占比关系。
分析选项D:条形图中白色直条最高,灰色直条和深灰色直条高度相近且较矮,不符合扇形统计图中各部分占比关系。
答案:B。
观察扇形统计图可知,灰色部分占比最大,白色部分次之,深灰色部分占比最小。
分析选项A:条形图中白色直条最高,灰色直条次之,深灰色直条最矮,不符合扇形统计图中各部分占比关系。
分析选项B:条形图中灰色直条最高,白色直条次之,深灰色直条最矮,符合扇形统计图中各部分占比关系。
分析选项C:条形图中白色直条最高,深灰色直条次之,灰色直条最矮,不符合扇形统计图中各部分占比关系。
分析选项D:条形图中白色直条最高,灰色直条和深灰色直条高度相近且较矮,不符合扇形统计图中各部分占比关系。
答案:B。
4.(云南丽江)某年级参加数学竞赛的女生和男生的人数比是1∶3,这次竞赛的平均成绩是82分,男生的平均成绩是80分。女生的平均成绩是(
A.82
B.84
C.86
D.88
D
)分。A.82
B.84
C.86
D.88
答案:
解析:本题考查的是平均数的应用。
可以使用赋值法,先假设女生的人数为1,男生的人数为3。
根据平均成绩=总成绩÷人数,可得:
总成绩=平均成绩×人数,
所以全体学生的总成绩为:
$82× (1+3)=328(分)$
男生的总成绩为:
$80 × 3 = 240(分)$
女生的总成绩为全体学生的总成绩减去男生的总成绩,即:
$328 - 240 = 88(分)$
因为女生的人数为1,所以女生的平均成绩就是女生的总成绩,即88分。
所以,女生的平均成绩是88分,答案为D。
可以使用赋值法,先假设女生的人数为1,男生的人数为3。
根据平均成绩=总成绩÷人数,可得:
总成绩=平均成绩×人数,
所以全体学生的总成绩为:
$82× (1+3)=328(分)$
男生的总成绩为:
$80 × 3 = 240(分)$
女生的总成绩为全体学生的总成绩减去男生的总成绩,即:
$328 - 240 = 88(分)$
因为女生的人数为1,所以女生的平均成绩就是女生的总成绩,即88分。
所以,女生的平均成绩是88分,答案为D。
查看更多完整答案,请扫码查看


