2025年名校优录小升初总复习六年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年名校优录小升初总复习六年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
6.(福建莆田)在$0.\dot{8}\dot{3}$、$0.8\dot{3}$、$\frac{21}{25}$、83.3%、$\frac{11}{25}$这四个数中,最小的数是(
A.$0.\dot{8}\dot{3}$
B.$0.8\dot{3}$
C.$\frac{21}{25}$
D.$\frac{11}{25}$
D
)。A.$0.\dot{8}\dot{3}$
B.$0.8\dot{3}$
C.$\frac{21}{25}$
D.$\frac{11}{25}$
答案:
解析:本题考查了小数、分数、百分数之间的大小比较。需要先将所有数转换为相同的形式(小数形式),再进行比较。
$0.\dot{8}\dot{3}$ 是一个循环小数,表示 $0.838383...$。
$0.8\dot{3}$ 也是一个循环小数,表示 $0.833333...$。
$\frac{21}{25}$ 是一个分数,转换为小数是 $0.84$。
$83.3\%$ 是一个百分数,转换为小数是 $0.833$。
$\frac{11}{25}$ 是一个分数,转换为小数是 $0.44$。
现在,比较这些小数的大小:
$0.44 < 0.833 < 0.833333... < 0.838383... < 0.84$,
即:
$\frac{11}{25} < 83.3\% < 0.8\dot{3} < 0.\dot{8}\dot{3} < \frac{21}{25}$,
从上面的比较中,可以看出最小的数是 $\frac{11}{25}$。
答案:D. $\frac{11}{25}$。
$0.\dot{8}\dot{3}$ 是一个循环小数,表示 $0.838383...$。
$0.8\dot{3}$ 也是一个循环小数,表示 $0.833333...$。
$\frac{21}{25}$ 是一个分数,转换为小数是 $0.84$。
$83.3\%$ 是一个百分数,转换为小数是 $0.833$。
$\frac{11}{25}$ 是一个分数,转换为小数是 $0.44$。
现在,比较这些小数的大小:
$0.44 < 0.833 < 0.833333... < 0.838383... < 0.84$,
即:
$\frac{11}{25} < 83.3\% < 0.8\dot{3} < 0.\dot{8}\dot{3} < \frac{21}{25}$,
从上面的比较中,可以看出最小的数是 $\frac{11}{25}$。
答案:D. $\frac{11}{25}$。
7.分子与分母的和是15的最简真分数有(
A.4
B.5
C.6
D.7
A
)个。A.4
B.5
C.6
D.7
答案:
分子与分母的和是15的真分数,分子小于分母,分子可取1-7。
分子=1,分母=14,分数=1/14,1和14互质,是最简真分数。
分子=2,分母=13,分数=2/13,2和13互质,是最简真分数。
分子=3,分母=12,分数=3/12,3和12有公因数3,不是最简真分数。
分子=4,分母=11,分数=4/11,4和11互质,是最简真分数。
分子=5,分母=10,分数=5/10,5和10有公因数5,不是最简真分数。
分子=6,分母=9,分数=6/9,6和9有公因数3,不是最简真分数。
分子=7,分母=8,分数=7/8,7和8互质,是最简真分数。
符合条件的最简真分数有1/14、2/13、4/11、7/8,共4个。
答案:A
分子=1,分母=14,分数=1/14,1和14互质,是最简真分数。
分子=2,分母=13,分数=2/13,2和13互质,是最简真分数。
分子=3,分母=12,分数=3/12,3和12有公因数3,不是最简真分数。
分子=4,分母=11,分数=4/11,4和11互质,是最简真分数。
分子=5,分母=10,分数=5/10,5和10有公因数5,不是最简真分数。
分子=6,分母=9,分数=6/9,6和9有公因数3,不是最简真分数。
分子=7,分母=8,分数=7/8,7和8互质,是最简真分数。
符合条件的最简真分数有1/14、2/13、4/11、7/8,共4个。
答案:A
8.著名的哥德巴赫猜想:任一大于2的偶数都可写成两个质数之和。下面与哥德巴赫猜想符合的是(
A.$60= 43+17$
B.$84= 3+81$
C.$100= 5+95$
D.$70= 5+65$
A
)。A.$60= 43+17$
B.$84= 3+81$
C.$100= 5+95$
D.$70= 5+65$
答案:
解析:本题考查对哥德巴赫猜想的理解以及质数的认识。哥德巴赫猜想指出任一大于 2 的偶数都可写成两个质数之和,所以需要判断每个选项中两个数是否为质数。
质数是指在大于 1 的自然数中,除了 1 和它本身以外不再有其他因数的自然数。
选项 A:$43$ 的因数只有$1$和$43$,$17$的因数只有$1$和$17$,$43$和$17$都是质数,且$60$是大于$2$的偶数,$60 = 43 + 17$符合哥德巴赫猜想。
选项 B:$81$的因数有$1$、$3$、$9$、$27$、$81$,$81$不是质数,所以$84 = 3 + 81$不符合哥德巴赫猜想。
选项 C:$95$的因数有$1$、$5$、$19$、$95$,$95$不是质数,所以$100 = 5 + 95$不符合哥德巴赫猜想。
选项 D:$65$的因数有$1$、$5$、$13$、$65$,$65$不是质数,所以$70 = 5 + 65$不符合哥德巴赫猜想。
答案:A。
质数是指在大于 1 的自然数中,除了 1 和它本身以外不再有其他因数的自然数。
选项 A:$43$ 的因数只有$1$和$43$,$17$的因数只有$1$和$17$,$43$和$17$都是质数,且$60$是大于$2$的偶数,$60 = 43 + 17$符合哥德巴赫猜想。
选项 B:$81$的因数有$1$、$3$、$9$、$27$、$81$,$81$不是质数,所以$84 = 3 + 81$不符合哥德巴赫猜想。
选项 C:$95$的因数有$1$、$5$、$19$、$95$,$95$不是质数,所以$100 = 5 + 95$不符合哥德巴赫猜想。
选项 D:$65$的因数有$1$、$5$、$13$、$65$,$65$不是质数,所以$70 = 5 + 65$不符合哥德巴赫猜想。
答案:A。
1.每个数中的“6”都表示什么?连一连。(10分)


答案:
本题可根据数位顺序表,确定每个数中“6”所在的数位,进而判断其表示的含义,再进行连线。
分析每个数中“6”表示的含义
6154000000:“6”在十亿位上,计数单位是十亿,所以它表示6个十亿。
46273580:“6”在百万位上,计数单位是百万,所以它表示6个百万。
3560000:“6”在万位上,计数单位是万,所以它表示6个万。
1586310:“6”在千位上,计数单位是千,所以它表示6个千。
3657800000:“6”在亿位上,计数单位是亿,所以它表示6个亿。
连线
将“6154000000”与“6个十亿”相连;
将“46273580”与“6个百万”相连;
将“3560000”与“6个万”相连;
将“1586310”与“6个千”相连;
将“3657800000”与“6个亿”相连。
分析每个数中“6”表示的含义
6154000000:“6”在十亿位上,计数单位是十亿,所以它表示6个十亿。
46273580:“6”在百万位上,计数单位是百万,所以它表示6个百万。
3560000:“6”在万位上,计数单位是万,所以它表示6个万。
1586310:“6”在千位上,计数单位是千,所以它表示6个千。
3657800000:“6”在亿位上,计数单位是亿,所以它表示6个亿。
连线
将“6154000000”与“6个十亿”相连;
将“46273580”与“6个百万”相连;
将“3560000”与“6个万”相连;
将“1586310”与“6个千”相连;
将“3657800000”与“6个亿”相连。
| 小数 | 分数 | 百分数 |
| 0.75 |
|
|
| 0.75 |
$\frac{3}{4}$
| $75\%$
||
1.375
| $1\frac{3}{8}$ | $137.5\%$
||
0.02
| $\frac{1}{50}$
| $2\%$ |
答案:
解析:本题主要考查小数、分数、百分数之间的互化。
小数化成分数:原来有几位小数,就在$1$的后面写几个零作分母,把原来的小数去掉小数点作分子,能约分的要约分。
分数化成小数:用分母去除分子。能除尽的就化成有限小数,有的不能除尽,不能化成有限小数的,一般保留三位小数。
小数化成百分数:只要把小数点向右移动两位,同时在后面添上百分号。
百分数化成小数:把百分数化成小数,只要把百分号去掉,同时把小数点向左移动两位。
分数化成百分数:通常先把分数化成小数(除不尽时,一般保留三位小数),再把小数化成百分数。
百分数化成分数:先把百分数改写成分数,能约分的要约成最简分数。
第一行:
小数$0.75$,化为分数:$\frac{75}{100}=\frac{3}{4}$,化为百分数:$0.75×100\%=75\%$。
第二行:
分数$1\frac{3}{8}$,化为小数:$1\frac{3}{8}=1+3÷8=1+0.375=1.375$,化为百分数:$1.375×100\%=137.5\%$。
第三行:
百分数$2\%$,化为小数:$2÷100=0.02$,化为分数:$\frac{2}{100}=\frac{1}{50}$。
答案:
| 小数 | 分数 | 百分数 |
| 0.75 | $\frac{3}{4}$ | $75\%$ |
| 1.375 | $1\frac{3}{8}$ | $137.5\%$ |
| 0.02 | $\frac{1}{50}$ | $2\%$ |
小数化成分数:原来有几位小数,就在$1$的后面写几个零作分母,把原来的小数去掉小数点作分子,能约分的要约分。
分数化成小数:用分母去除分子。能除尽的就化成有限小数,有的不能除尽,不能化成有限小数的,一般保留三位小数。
小数化成百分数:只要把小数点向右移动两位,同时在后面添上百分号。
百分数化成小数:把百分数化成小数,只要把百分号去掉,同时把小数点向左移动两位。
分数化成百分数:通常先把分数化成小数(除不尽时,一般保留三位小数),再把小数化成百分数。
百分数化成分数:先把百分数改写成分数,能约分的要约成最简分数。
第一行:
小数$0.75$,化为分数:$\frac{75}{100}=\frac{3}{4}$,化为百分数:$0.75×100\%=75\%$。
第二行:
分数$1\frac{3}{8}$,化为小数:$1\frac{3}{8}=1+3÷8=1+0.375=1.375$,化为百分数:$1.375×100\%=137.5\%$。
第三行:
百分数$2\%$,化为小数:$2÷100=0.02$,化为分数:$\frac{2}{100}=\frac{1}{50}$。
答案:
| 小数 | 分数 | 百分数 |
| 0.75 | $\frac{3}{4}$ | $75\%$ |
| 1.375 | $1\frac{3}{8}$ | $137.5\%$ |
| 0.02 | $\frac{1}{50}$ | $2\%$ |
3.将下面每组数进行通分,并比较大小。(8分)
$\frac{5}{8}和\frac{7}{12}$
$\frac{4}{9}和\frac{5}{11}$
$\frac{5}{8}和\frac{7}{12}$
$\frac{4}{9}和\frac{5}{11}$
答案:
解析:
题目考查的是分数的通分以及分数大小的比较。
通分的关键是找到两个分数分母的最小公倍数,然后将两个分数转化为以这个最小公倍数为分母的形式。
比较两个分数大小时,如果它们的分母相同,则比较分子,分子大的分数就大。
答案:
(1) 对于 $\frac{5}{8}$ 和 $\frac{7}{12}$:
首先求8和12的最小公倍数,为24。
$\frac{5}{8} = \frac{5 × 3}{8 × 3} = \frac{15}{24}$
$\frac{7}{12} = \frac{7 × 2}{12 × 2} = \frac{14}{24}$
因为 $\frac{15}{24} > \frac{14}{24}$,所以 $\frac{5}{8} > \frac{7}{12}$。
(2) 对于 $\frac{4}{9}$ 和 $\frac{5}{11}$:
首先求9和11的最小公倍数,为99。
$\frac{4}{9} = \frac{4 × 11}{9 × 11} = \frac{44}{99}$
$\frac{5}{11} = \frac{5 × 9}{11 × 9} = \frac{45}{99}$
因为 $\frac{44}{99} < \frac{45}{99}$,所以 $\frac{4}{9} < \frac{5}{11}$。
题目考查的是分数的通分以及分数大小的比较。
通分的关键是找到两个分数分母的最小公倍数,然后将两个分数转化为以这个最小公倍数为分母的形式。
比较两个分数大小时,如果它们的分母相同,则比较分子,分子大的分数就大。
答案:
(1) 对于 $\frac{5}{8}$ 和 $\frac{7}{12}$:
首先求8和12的最小公倍数,为24。
$\frac{5}{8} = \frac{5 × 3}{8 × 3} = \frac{15}{24}$
$\frac{7}{12} = \frac{7 × 2}{12 × 2} = \frac{14}{24}$
因为 $\frac{15}{24} > \frac{14}{24}$,所以 $\frac{5}{8} > \frac{7}{12}$。
(2) 对于 $\frac{4}{9}$ 和 $\frac{5}{11}$:
首先求9和11的最小公倍数,为99。
$\frac{4}{9} = \frac{4 × 11}{9 × 11} = \frac{44}{99}$
$\frac{5}{11} = \frac{5 × 9}{11 × 9} = \frac{45}{99}$
因为 $\frac{44}{99} < \frac{45}{99}$,所以 $\frac{4}{9} < \frac{5}{11}$。
1.玲玲在写数时,不小心把一个数的千位与万位上的数字交换了位置,百万位和十万位上的数字交换了位置,写成了6240539。这个数原来是多少?读作多少?(4分)
答案:
写作:2604539
读作:二百六十万四千五百三十九
读作:二百六十万四千五百三十九
2.下面的数轴1格表示200米,刚开始汽车的位置在0处。(4分)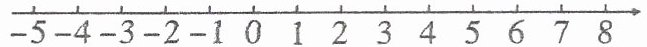
(1)如果从0处向东行驶8格表示$+1600$米,那么从0处开始向西行驶5格,应表示为(
(2)如果汽车的最终位置在$-6$处,说明它向(
(3)如果汽车先向东行驶7格,再向西行驶10格,这时汽车的位置表示为(
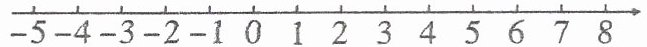
(1)如果从0处向东行驶8格表示$+1600$米,那么从0处开始向西行驶5格,应表示为(
-1000
)米。(2)如果汽车的最终位置在$-6$处,说明它向(
西
)行驶了(1200
)米。(3)如果汽车先向东行驶7格,再向西行驶10格,这时汽车的位置表示为(
-600
)米。
答案:
(1)
解析:已知每格表示200米,向西行驶5格,就是$200×5 = 1000$(米),且向西为负方向。
答案:$-1000$
(2)
解析:因为负号表示向西,位置在$- 6$处,每格200米,所以行驶的距离是$200×6=1200$(米)。
答案:西;1200
(3)
解析:向东行驶7格,位置是$200×7 = 1400$(米),即$+1400$米;再向西行驶10格,位置是$200×10=2000$(米),即$-2000$米。最终位置是$1400 - 2000=-600$(米)。
答案:$-600$
(1)
解析:已知每格表示200米,向西行驶5格,就是$200×5 = 1000$(米),且向西为负方向。
答案:$-1000$
(2)
解析:因为负号表示向西,位置在$- 6$处,每格200米,所以行驶的距离是$200×6=1200$(米)。
答案:西;1200
(3)
解析:向东行驶7格,位置是$200×7 = 1400$(米),即$+1400$米;再向西行驶10格,位置是$200×10=2000$(米),即$-2000$米。最终位置是$1400 - 2000=-600$(米)。
答案:$-600$
3.某商店有三种数量相同的冷饮,星期六的销售情况如下:
冰淇淋 售出$\frac{7}{8}$
果汁 售出$\frac{3}{4}$
可乐 售出$\frac{5}{16}$
如果这个商店要进货,应多进哪种冷饮?为什么?(4分)
冰淇淋 售出$\frac{7}{8}$
果汁 售出$\frac{3}{4}$
可乐 售出$\frac{5}{16}$

如果这个商店要进货,应多进哪种冷饮?为什么?(4分)
答案:
解析:题目考查分数的大小比较这一知识点。要判断商店应多进哪种冷饮,需比较三种冷饮的售出比例,售出比例高的冷饮更受欢迎,应多进货。比较分数大小时,先通分,再比较分子大小。
答案:
$\frac{7}{8}=\frac{7×2}{8×2}=\frac{14}{16}$
$\frac{3}{4}=\frac{3×4}{4×4}=\frac{12}{16}$
因为$\frac{14}{16}>\frac{12}{16}>\frac{5}{16}$,即$\frac{7}{8}>\frac{3}{4}>\frac{5}{16}$。
所以应多进冰淇淋,因为冰淇淋的售出比例最高。
答案:
$\frac{7}{8}=\frac{7×2}{8×2}=\frac{14}{16}$
$\frac{3}{4}=\frac{3×4}{4×4}=\frac{12}{16}$
因为$\frac{14}{16}>\frac{12}{16}>\frac{5}{16}$,即$\frac{7}{8}>\frac{3}{4}>\frac{5}{16}$。
所以应多进冰淇淋,因为冰淇淋的售出比例最高。
4.一块正方形布料,既可以做成边长是18厘米的小正方形手帕,又可以做成边长是30厘米的大正方形手帕,都没有剩余。这块正方形布料的边长至少是多少厘米?(5分)
答案:
解析:本题考查最小公倍数的应用。
要求这块正方形布料的边长至少是多少厘米,即是求18和30的最小公倍数。
对18和30分解质因数:
$18=2×3×3$,
$30=2×3×5$,
所以18和30的最小公倍数为:
$2×3×3×5=90$,
答案:这块正方形布料的边长至少是90厘米。
要求这块正方形布料的边长至少是多少厘米,即是求18和30的最小公倍数。
对18和30分解质因数:
$18=2×3×3$,
$30=2×3×5$,
所以18和30的最小公倍数为:
$2×3×3×5=90$,
答案:这块正方形布料的边长至少是90厘米。
查看更多完整答案,请扫码查看


