2025年名校优录小升初总复习六年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年名校优录小升初总复习六年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
5.一个圆柱和一个圆锥,底面半径之比是2:3,体积之比是5:6,那么圆柱与圆锥的高之比是(
A.5:8
B.8:5
C.15:8
D.8:15
A
)。A.5:8
B.8:5
C.15:8
D.8:15
答案:
解析:
本题考查圆柱与圆锥的体积公式。
圆柱的体积公式为$V_{cylinder} = \pi r_{1}^{2} h_{1}$,圆锥的体积公式为$V_{cone} = \frac{1}{3} \pi r_{2}^{2} h_{2}$。
根据题目,底面半径之比是2:3,设圆柱的底面半径为$2k$,圆锥的底面半径为$3k$;体积之比是5:6,设圆柱的体积为$5m$,圆锥的体积为$6m$。
将这些值代入体积公式,可以得到以下等式:
对于圆柱:$5m = \pi (2k)^{2} h_{1} = 4\pi k^{2} h_{1}$。
对于圆锥:$6m = \frac{1}{3} \pi (3k)^{2} h_{2} = 3\pi k^{2} h_{2}$。
解这两个等式,找出$h_{1}$和$h_{2}$的比值。
从圆柱的体积等式,得到$h_{1} = \frac{5m}{4\pi k^{2}}$。
从圆锥的体积等式,得到$h_{2} = \frac{6m}{3\pi k^{2}} = \frac{2m}{\pi k^{2}}$。
因此,圆柱与圆锥的高之比为:
$\frac{h_{1}}{h_{2}} = \frac{\frac{5m}{4\pi k^{2}}}{\frac{2m}{\pi k^{2}}} = \frac{5}{8}$。
所以,圆柱与圆锥的高之比是5:8。
答案:A
本题考查圆柱与圆锥的体积公式。
圆柱的体积公式为$V_{cylinder} = \pi r_{1}^{2} h_{1}$,圆锥的体积公式为$V_{cone} = \frac{1}{3} \pi r_{2}^{2} h_{2}$。
根据题目,底面半径之比是2:3,设圆柱的底面半径为$2k$,圆锥的底面半径为$3k$;体积之比是5:6,设圆柱的体积为$5m$,圆锥的体积为$6m$。
将这些值代入体积公式,可以得到以下等式:
对于圆柱:$5m = \pi (2k)^{2} h_{1} = 4\pi k^{2} h_{1}$。
对于圆锥:$6m = \frac{1}{3} \pi (3k)^{2} h_{2} = 3\pi k^{2} h_{2}$。
解这两个等式,找出$h_{1}$和$h_{2}$的比值。
从圆柱的体积等式,得到$h_{1} = \frac{5m}{4\pi k^{2}}$。
从圆锥的体积等式,得到$h_{2} = \frac{6m}{3\pi k^{2}} = \frac{2m}{\pi k^{2}}$。
因此,圆柱与圆锥的高之比为:
$\frac{h_{1}}{h_{2}} = \frac{\frac{5m}{4\pi k^{2}}}{\frac{2m}{\pi k^{2}}} = \frac{5}{8}$。
所以,圆柱与圆锥的高之比是5:8。
答案:A
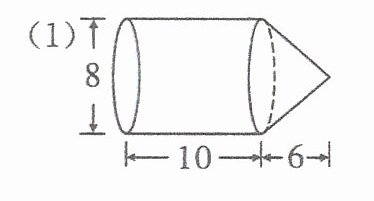
1.求下面各立体图形的体积。(单位:cm)
(1)
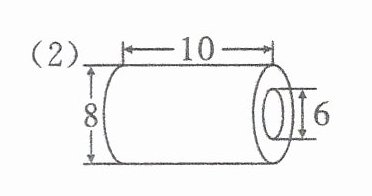
(2)
(1)

(2)

答案:
(1)圆柱体积:$3.14×(8÷2)^2×10 = 3.14×16×10 = 502.4$($cm^3$)
圆锥体积:$\frac{1}{3}×3.14×(8÷2)^2×6 = \frac{1}{3}×3.14×16×6 = 100.48$($cm^3$)
总体积:$502.4 + 100.48 = 602.88$($cm^3$)
(2)外圆柱体积:$3.14×(8÷2)^2×10 = 3.14×16×10 = 502.4$($cm^3$)
内圆柱体积:$3.14×(6÷2)^2×10 = 3.14×9×10 = 282.6$($cm^3$)
体积:$502.4 - 282.6 = 219.8$($cm^3$)
(1)圆柱体积:$3.14×(8÷2)^2×10 = 3.14×16×10 = 502.4$($cm^3$)
圆锥体积:$\frac{1}{3}×3.14×(8÷2)^2×6 = \frac{1}{3}×3.14×16×6 = 100.48$($cm^3$)
总体积:$502.4 + 100.48 = 602.88$($cm^3$)
(2)外圆柱体积:$3.14×(8÷2)^2×10 = 3.14×16×10 = 502.4$($cm^3$)
内圆柱体积:$3.14×(6÷2)^2×10 = 3.14×9×10 = 282.6$($cm^3$)
体积:$502.4 - 282.6 = 219.8$($cm^3$)
2.计算下面图形的表面积。(单位:dm)


答案:
3.14×4×3 + 3.14×(4÷2)²×2 + 3.14×1×2 = 69.08(dm²)
1.(安徽合肥)压路机的滚筒是一个圆柱,它的底面周长是3.14米,长是1.5米,每滚动一周能压多大面积的路面?如果它滚动20周,压路的面积是多少?
答案:
每滚动一周压路面积:3.14×1.5=4.71(平方米)
滚动20周压路面积:4.71×20=94.2(平方米)
答:每滚动一周能压4.71平方米的路面,滚动20周压路的面积是94.2平方米。
滚动20周压路面积:4.71×20=94.2(平方米)
答:每滚动一周能压4.71平方米的路面,滚动20周压路的面积是94.2平方米。
2.(四川内江)如图,用铁丝做一个底面半径10 cm、高30 cm的圆柱形灯笼框架(侧面共有4根铁丝,用来连接上、下两个面)。至少需要铁丝多少厘米?如果在灯笼框架侧面包一层红布,至少需要多少平方厘米的红布?
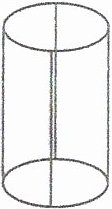

答案:
求至少需要铁丝多少厘米:
圆柱底面周长:$2×3.14×10 = 62.8$(cm)
上、下底面铁丝总长:$62.8×2 = 125.6$(cm)
侧面铁丝总长:$30×4 = 120$(cm)
铁丝总长:$125.6 + 120 = 245.6$(cm)
求至少需要红布多少平方厘米:
圆柱侧面积:$2×3.14×10×30 = 1884$(cm²)
答:至少需要铁丝245.6厘米,至少需要1884平方厘米的红布。
圆柱底面周长:$2×3.14×10 = 62.8$(cm)
上、下底面铁丝总长:$62.8×2 = 125.6$(cm)
侧面铁丝总长:$30×4 = 120$(cm)
铁丝总长:$125.6 + 120 = 245.6$(cm)
求至少需要红布多少平方厘米:
圆柱侧面积:$2×3.14×10×30 = 1884$(cm²)
答:至少需要铁丝245.6厘米,至少需要1884平方厘米的红布。
3.(湖北荆州)如图,一个底面直径是20 cm的圆柱形水杯里浸没着一个底面半径是3 cm的圆锥形铅锤。当取出铅锤时,圆柱形水杯里的水下降0.6 cm。求这个圆锥的高。


答案:
解析:本题考查圆柱和圆锥体积的计算。
先根据圆柱体积公式$V = \pi r^2h$(其中$V$是体积,$r$是底面半径,$h$是高)求出下降的水的体积,这个体积就是圆锥形铅锤的体积。
再根据圆锥体积公式$V=\frac{1}{3}\pi r^2h$(其中$V$是体积,$r$是底面半径,$h$是高)求出圆锥的高。
圆柱底面直径是$20cm$,则半径为$20÷2 = 10cm$,水下降了$0.6cm$,下降的水的体积为:
$V_{圆柱}=\pi×10^2×0.6 = 60\pi(cm^3)$。
因为下降的水的体积等于圆锥形铅锤的体积,所以$V_{圆锥}= 60\pi cm^3$。
圆锥底面半径是$3cm$,根据圆锥体积公式$V=\frac{1}{3}\pi r^2h$可得:
$60\pi=\frac{1}{3}\pi×3^2× h$,
两边同时除以$\pi$得:
$60=\frac{1}{3}×3^2× h$,
$60 = 3h$,
解得$h = 20$。
答案:这个圆锥的高是$20cm$。
先根据圆柱体积公式$V = \pi r^2h$(其中$V$是体积,$r$是底面半径,$h$是高)求出下降的水的体积,这个体积就是圆锥形铅锤的体积。
再根据圆锥体积公式$V=\frac{1}{3}\pi r^2h$(其中$V$是体积,$r$是底面半径,$h$是高)求出圆锥的高。
圆柱底面直径是$20cm$,则半径为$20÷2 = 10cm$,水下降了$0.6cm$,下降的水的体积为:
$V_{圆柱}=\pi×10^2×0.6 = 60\pi(cm^3)$。
因为下降的水的体积等于圆锥形铅锤的体积,所以$V_{圆锥}= 60\pi cm^3$。
圆锥底面半径是$3cm$,根据圆锥体积公式$V=\frac{1}{3}\pi r^2h$可得:
$60\pi=\frac{1}{3}\pi×3^2× h$,
两边同时除以$\pi$得:
$60=\frac{1}{3}×3^2× h$,
$60 = 3h$,
解得$h = 20$。
答案:这个圆锥的高是$20cm$。
4.(湖北黄冈)我们曾经用下面的方法解决了求三角形面积的问题,用这样的经验,你能求出下面右图中这个几何体的体积吗?把你的想法画成草图标并列式计算。(单位:cm)


答案:
将两个完全相同的该几何体拼成一个底面直径20cm、高(15+25)cm的圆柱。
圆柱体积:$3.14×(20÷2)^2×(15+25)=3.14×100×40=12560(cm^3)$
所求几何体体积:$12560÷2=6280(cm^3)$
答案:$\boxed{6280}$
圆柱体积:$3.14×(20÷2)^2×(15+25)=3.14×100×40=12560(cm^3)$
所求几何体体积:$12560÷2=6280(cm^3)$
答案:$\boxed{6280}$
查看更多完整答案,请扫码查看


