2025年名校优录小升初总复习六年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年名校优录小升初总复习六年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 师傅每小时加工 y 个零件,徒弟每小时比师傅少加工 5 个。y-5 表示(
徒弟每小时加工零件的个数
),5(y-5)表示(徒弟5小时加工零件的个数
)。
答案:
解析:题目考查了用字母表示数以及含有字母式子的含义。对于$y - 5$,因为徒弟每小时比师傅少加工$5$个,师傅每小时加工$y$个零件,所以$y - 5$表示徒弟每小时加工零件的个数;对于$5(y - 5)$,$y - 5$是徒弟每小时加工零件的个数,那么$5(y - 5)$就表示徒弟$5$小时加工零件的个数。
答案:徒弟每小时加工零件的个数;徒弟$5$小时加工零件的个数。
答案:徒弟每小时加工零件的个数;徒弟$5$小时加工零件的个数。
2. 一本书共有 m 页,小明每天看 a 页,看了 b 天,还剩 19 页,小明看了(
ab
)页,还可以表示为(m - 19
)页。
答案:
解析:
本题主要考查用字母表示数以及简单的代数运算。
首先,小明每天看$a$页,看了$b$天,所以他总共看了 $a × b$ 页,即 $ab$ 页。
然后,题目说这本书共有$m$页,还剩19页没有看。
因此,小明已经看过的页数和还未看的页数之和应该等于书的总页数。
即:$ab + 19 = m$,
由此,可以得出小明已经看过的页数为 $ab$,
同时,这个表达式还可以表示为 $m - 19$,因为 $m - 19$ 就是小明已经看过的页数。
答案:
$ab$;$m - 19$。
本题主要考查用字母表示数以及简单的代数运算。
首先,小明每天看$a$页,看了$b$天,所以他总共看了 $a × b$ 页,即 $ab$ 页。
然后,题目说这本书共有$m$页,还剩19页没有看。
因此,小明已经看过的页数和还未看的页数之和应该等于书的总页数。
即:$ab + 19 = m$,
由此,可以得出小明已经看过的页数为 $ab$,
同时,这个表达式还可以表示为 $m - 19$,因为 $m - 19$ 就是小明已经看过的页数。
答案:
$ab$;$m - 19$。
3. 桶里原来有 3 千克水,又加入 5 勺,每勺 x 千克。桶里现在有水
3 + 5x
千克,当 x= 0.2 时,桶里一共有水4
千克。
答案:
解析:
本题主要考查用字母表示数以及代数式的求值。
首先,桶里原来有3千克水,又加入了5勺水,每勺x千克,所以加入的水的总重量是$5x$千克。
那么,桶里现在的水总重量就是原来的水重量加上新加入的水重量,即$(3 + 5x)$千克。
然后,当$x = 0.2$时,代入上述表达式,就可以得到桶里现在的水总重量。
即:
$3 + 5 × 0.2 = 4$
所以,桶里现在有水$(3 + 5x)$千克,当$x = 0.2$时,桶里一共有水4千克。
答案:
桶里现在有水$(3 + 5x)$千克;当$x = 0.2$时,桶里一共有水4千克。
本题主要考查用字母表示数以及代数式的求值。
首先,桶里原来有3千克水,又加入了5勺水,每勺x千克,所以加入的水的总重量是$5x$千克。
那么,桶里现在的水总重量就是原来的水重量加上新加入的水重量,即$(3 + 5x)$千克。
然后,当$x = 0.2$时,代入上述表达式,就可以得到桶里现在的水总重量。
即:
$3 + 5 × 0.2 = 4$
所以,桶里现在有水$(3 + 5x)$千克,当$x = 0.2$时,桶里一共有水4千克。
答案:
桶里现在有水$(3 + 5x)$千克;当$x = 0.2$时,桶里一共有水4千克。
4. 分数$\frac{a}{15}$(a 是大于零的自然数),当 a 等于(
14
)时,$\frac{a}{15}$是最大真分数;当 a 大于或等于(15
)时,$\frac{a}{15}$是假分数。
答案:
14;15
5. 如果$4x+20= 100$,那么$7x-60= $
80
。
答案:
解析:本题可先根据等式的性质求出方程$4x + 20 = 100$中$x$的值,再将$x$的值代入$7x - 60$中计算结果。
答案:
解:$4x + 20 = 100$
$4x=100 - 20$
$4x = 80$
$x = 80÷4$
$x = 20$
把$x = 20$代入$7x - 60$可得:
$7×20 - 60$
$=140 - 60$
$= 80$
故答案为$80$。
答案:
解:$4x + 20 = 100$
$4x=100 - 20$
$4x = 80$
$x = 80÷4$
$x = 20$
把$x = 20$代入$7x - 60$可得:
$7×20 - 60$
$=140 - 60$
$= 80$
故答案为$80$。
6. 当$a= \frac{1}{2}$,$b= \frac{4}{5}$时,$2a+5b$的值是(
5
)。
答案:
解析:本题考查代数式的求值,直接将$a$、$b$的值代入式子进行计算。
答案:
当$a = \frac{1}{2}$,$b = \frac{4}{5}$时,
$2a + 5b$
$= 2×\frac{1}{2}+5×\frac{4}{5}$
$= 1 + 4$
$= 5$
故答案为$5$。
答案:
当$a = \frac{1}{2}$,$b = \frac{4}{5}$时,
$2a + 5b$
$= 2×\frac{1}{2}+5×\frac{4}{5}$
$= 1 + 4$
$= 5$
故答案为$5$。
7. 下图是由两个边长分别为 a、b 的正方形拼成的。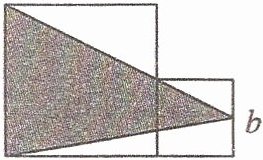
(1)用含字母的式子表示图中阴影部分的面积是(
(2)当$a= 5\ cm$,$b= 4\ cm$时,阴影部分的面积是(

(1)用含字母的式子表示图中阴影部分的面积是(
$\frac{1}{2}(a^2 + b^2 - ab)$
)。(2)当$a= 5\ cm$,$b= 4\ cm$时,阴影部分的面积是(
10.5
)$cm^2$。
答案:
(1) 两个正方形边长分别为 $a$ 和 $b$。
整个图形的面积是 $a^2 + b^2$。
非阴影部分包括一个边长为 $a$ 的三角形和一个边长为 $b$ 的三角形。
边长为 $a$ 的三角形的面积为 $\frac{1}{2} × a × a = \frac{1}{2}a^2$。
边长为 $b$ 的三角形的面积为 $\frac{1}{2} × b × (a + b) = \frac{1}{2}b(a + b)$。
所以,阴影部分的面积为:
$ a^2 + b^2 - \frac{1}{2}a^2 - \frac{1}{2}b(a + b) $
$ = \frac{1}{2}a^2 + \frac{1}{2}b^2 - \frac{1}{2}ab $
$ = \frac{1}{2}(a^2 + b^2 - ab) $
本题应填:$\frac{1}{2}(a^2 + b^2 - ab) $。
(2) 将 $a = 5cm$ 和 $b = 4cm$ 带入阴影部分的面积公式:
$ \frac{1}{2}(a^2 + b^2 - ab) $
$ = \frac{1}{2}(5^2 + 4^2 - 5 × 4) $
$ = \frac{1}{2}(25 + 16 - 20) $
$ = \frac{1}{2} × 21 $
$ = 10.5 (cm^2) $
本题应填:$10.5 cm^2$。
(1) 两个正方形边长分别为 $a$ 和 $b$。
整个图形的面积是 $a^2 + b^2$。
非阴影部分包括一个边长为 $a$ 的三角形和一个边长为 $b$ 的三角形。
边长为 $a$ 的三角形的面积为 $\frac{1}{2} × a × a = \frac{1}{2}a^2$。
边长为 $b$ 的三角形的面积为 $\frac{1}{2} × b × (a + b) = \frac{1}{2}b(a + b)$。
所以,阴影部分的面积为:
$ a^2 + b^2 - \frac{1}{2}a^2 - \frac{1}{2}b(a + b) $
$ = \frac{1}{2}a^2 + \frac{1}{2}b^2 - \frac{1}{2}ab $
$ = \frac{1}{2}(a^2 + b^2 - ab) $
本题应填:$\frac{1}{2}(a^2 + b^2 - ab) $。
(2) 将 $a = 5cm$ 和 $b = 4cm$ 带入阴影部分的面积公式:
$ \frac{1}{2}(a^2 + b^2 - ab) $
$ = \frac{1}{2}(5^2 + 4^2 - 5 × 4) $
$ = \frac{1}{2}(25 + 16 - 20) $
$ = \frac{1}{2} × 21 $
$ = 10.5 (cm^2) $
本题应填:$10.5 cm^2$。
8. 三个连续自然数,中间一个是$a+2$,其余两个数是(
$a+1$
)和($a+3$
)。
答案:
解析:题目考查连续自然数的性质。对于任意三个连续自然数,如果知道其中一个数,那么其余两个数可以通过对这个数加减1来得到。题目已给出中间的一个数是$a+2$,那么前一个数就是$(a+2) - 1 = a+1$,后一个数就是$(a+2) + 1 = a+3$。
答案:$a+1$;$a+3$。
答案:$a+1$;$a+3$。
9. 已知$□+□= \star+\star+\star$,$\star+\star+□+□+□= 65$,则$\star=$(
10
),$□=$(15
)。
答案:
由$□+□=★+★+★$可得$2□=3★$,则$□=\frac{3}{2}★$。
将$□=\frac{3}{2}★$代入$★+★+□+□+□=65$,得:
$2★ + 3×\frac{3}{2}★=65$
$2★+\frac{9}{2}★=65$
$\frac{4}{2}★+\frac{9}{2}★=65$
$\frac{13}{2}★=65$
$★=65×\frac{2}{13}$
$★=10$
则$□=\frac{3}{2}×10=15$
$★=10$,$□=15$
将$□=\frac{3}{2}★$代入$★+★+□+□+□=65$,得:
$2★ + 3×\frac{3}{2}★=65$
$2★+\frac{9}{2}★=65$
$\frac{4}{2}★+\frac{9}{2}★=65$
$\frac{13}{2}★=65$
$★=65×\frac{2}{13}$
$★=10$
则$□=\frac{3}{2}×10=15$
$★=10$,$□=15$
二、判断题。(对的打“√”,错的打“×”)(每小题 2 分,共 12 分)
1. 使方程左右两边相等的未知数的值就是方程的解。(
2. 解$x-1.2= 9.6$时,方程的两边应同时减去 1.2。(
3. 一根绳子长 x 米,用去$\frac{1}{2}$,还剩$(x-\frac{1}{2})$米。(
4. 方程$2x-0.1= 1.08与方程(x+5)×2= 11.18$的解相同。(
5. 3 筐苹果重 a kg,则 5 筐苹果约重$(a÷3×5)\ kg$。(
6. 种树 a 棵,成活了 b 棵。这批树的成活率是$b÷(a+b)×100\%$。(
1. 使方程左右两边相等的未知数的值就是方程的解。(
√
)2. 解$x-1.2= 9.6$时,方程的两边应同时减去 1.2。(
×
)3. 一根绳子长 x 米,用去$\frac{1}{2}$,还剩$(x-\frac{1}{2})$米。(
×
)4. 方程$2x-0.1= 1.08与方程(x+5)×2= 11.18$的解相同。(
√
)5. 3 筐苹果重 a kg,则 5 筐苹果约重$(a÷3×5)\ kg$。(
√
)6. 种树 a 棵,成活了 b 棵。这批树的成活率是$b÷(a+b)×100\%$。(
×
)
答案:
解析:
1. 题目考查方程的解的定义,根据定义,使方程左右两边相等的未知数的值就是方程的解,所以此题正确。
答案:√
2. 题目考查解方程的方法,解$x-1.2= 9.6$时,应该将方程的两边同时加上$1.2$,使方程变为$x=10.8$,而不是同时减去$1.2$,所以此题错误。
答案:×
3. 题目考查分数的运算,一根绳子长$x$米,用去$\frac{1}{2}$,应该还剩$x × (1-\frac{1}{2})=\frac{1}{2}x$米,而不是$(x-\frac{1}{2})$米,所以此题错误。
答案:×
4. 题目考查解方程,对于方程$2x-0.1= 1.08$,可以解出$x=\frac{1.08+0.1}{2}=0.59$;对于方程$(x+5) × 2= 11.18$,可以解出$x=\frac{11.18}{2}-5=0.59$,两个方程的解相同,所以此题正确。
答案:√
5. 题目考查比例运算,3筐苹果重$a$ kg,则一筐苹果重$\frac{a}{3}$ kg,5筐苹果则重$5 × \frac{a}{3}=\frac{5a}{3}$ kg,也可以表示为$(a ÷ 3 × 5)$ kg,所以此题正确。
答案:√
6. 题目考查成活率的计算,成活率应该是成活的数量除以总的数量,即$成活率 = \frac{b}{a} × 100\%$,而不是$\frac{b}{a+b} × 100\%$,所以此题错误。
答案:×
1. 题目考查方程的解的定义,根据定义,使方程左右两边相等的未知数的值就是方程的解,所以此题正确。
答案:√
2. 题目考查解方程的方法,解$x-1.2= 9.6$时,应该将方程的两边同时加上$1.2$,使方程变为$x=10.8$,而不是同时减去$1.2$,所以此题错误。
答案:×
3. 题目考查分数的运算,一根绳子长$x$米,用去$\frac{1}{2}$,应该还剩$x × (1-\frac{1}{2})=\frac{1}{2}x$米,而不是$(x-\frac{1}{2})$米,所以此题错误。
答案:×
4. 题目考查解方程,对于方程$2x-0.1= 1.08$,可以解出$x=\frac{1.08+0.1}{2}=0.59$;对于方程$(x+5) × 2= 11.18$,可以解出$x=\frac{11.18}{2}-5=0.59$,两个方程的解相同,所以此题正确。
答案:√
5. 题目考查比例运算,3筐苹果重$a$ kg,则一筐苹果重$\frac{a}{3}$ kg,5筐苹果则重$5 × \frac{a}{3}=\frac{5a}{3}$ kg,也可以表示为$(a ÷ 3 × 5)$ kg,所以此题正确。
答案:√
6. 题目考查成活率的计算,成活率应该是成活的数量除以总的数量,即$成活率 = \frac{b}{a} × 100\%$,而不是$\frac{b}{a+b} × 100\%$,所以此题错误。
答案:×
1. 下面四种说法中,错误的是(
A.方程一定是等式
B.解方程是求方程的解的过程
C.$3x+\frac{1}{5}>0$是方程
D.$x+y= 1$是方程
C
)。A.方程一定是等式
B.解方程是求方程的解的过程
C.$3x+\frac{1}{5}>0$是方程
D.$x+y= 1$是方程
答案:
解析:本题主要考查方程的定义及解方程的概念。
选项A,根据方程的定义,方程就是含有未知数的等式,所以方程一定是等式,这个选项是正确的。
选项B,解方程确实是通过一定的运算,找出使方程成立的未知数的值,也就是求方程的解的过程,所以这个选项也是正确的。
选项C,$3x+\frac{1}{5}>0$,虽然它含有未知数$x$,但它是一个不等式,不是等式,所以不满足方程的定义,这个选项是错误的。
选项D,$x+y= 1$,它含有两个未知数$x$和$y$,并且是一个等式,所以满足方程的定义,这个选项是正确的。
答案:C。
选项A,根据方程的定义,方程就是含有未知数的等式,所以方程一定是等式,这个选项是正确的。
选项B,解方程确实是通过一定的运算,找出使方程成立的未知数的值,也就是求方程的解的过程,所以这个选项也是正确的。
选项C,$3x+\frac{1}{5}>0$,虽然它含有未知数$x$,但它是一个不等式,不是等式,所以不满足方程的定义,这个选项是错误的。
选项D,$x+y= 1$,它含有两个未知数$x$和$y$,并且是一个等式,所以满足方程的定义,这个选项是正确的。
答案:C。
2. 下列方程中,和方程$x-1= 4$的解相同的方程是(
A.$2x-3= 5$
B.$4x+1= 15$
C.$4x+4= 24$
D.$x+4= 5$
C
)。A.$2x-3= 5$
B.$4x+1= 15$
C.$4x+4= 24$
D.$x+4= 5$
答案:
解方程$x - 1 = 4$,得$x = 5$。
A. 解方程$2x - 3 = 5$,$2x = 5 + 3$,$2x = 8$,$x = 4$。
B. 解方程$4x + 1 = 15$,$4x = 15 - 1$,$4x = 14$,$x = 3.5$。
C. 解方程$4x + 4 = 24$,$4x = 24 - 4$,$4x = 20$,$x = 5$。
D. 解方程$x + 4 = 5$,$x = 5 - 4$,$x = 1$。
答案:C
A. 解方程$2x - 3 = 5$,$2x = 5 + 3$,$2x = 8$,$x = 4$。
B. 解方程$4x + 1 = 15$,$4x = 15 - 1$,$4x = 14$,$x = 3.5$。
C. 解方程$4x + 4 = 24$,$4x = 24 - 4$,$4x = 20$,$x = 5$。
D. 解方程$x + 4 = 5$,$x = 5 - 4$,$x = 1$。
答案:C
3. (河南焦作)工地上有 x 吨水泥,每天用 1.9 吨,用了 y 天,没用完。根据这些信息,不能求出问题(
A.还剩多少吨
B.y 天用了多少吨
C.实际比计划少用多少天
D.照这样计算,这些水泥一共可以用多少天
C
)。A.还剩多少吨
B.y 天用了多少吨
C.实际比计划少用多少天
D.照这样计算,这些水泥一共可以用多少天
答案:
解析:
A选项:还剩多少吨,可以通过$总水泥量 - 已用量 = x - 1.9y$来求得,所以A选项是可以求出的。
B选项:y天用了多少吨,可以通过$每天用量 × 天数 = 1.9y$来求得,所以B选项是可以求出的。
C选项:实际比计划少用多少天,这个选项需要知道计划用的天数和实际用的天数,但题目中只给出了实际用的天数y,没有给出计划用的天数,所以C选项是无法求出的。
D选项:照这样计算,这些水泥一共可以用多少天,可以通过$总水泥量 ÷ 每天用量 = \frac{x}{1.9}$来求得(结果向上取整,因为即使不够一天的量也需要一天来使用),所以D选项在理论上是可以求出的,只是需要一个向上取整的步骤。
答案:C。
A选项:还剩多少吨,可以通过$总水泥量 - 已用量 = x - 1.9y$来求得,所以A选项是可以求出的。
B选项:y天用了多少吨,可以通过$每天用量 × 天数 = 1.9y$来求得,所以B选项是可以求出的。
C选项:实际比计划少用多少天,这个选项需要知道计划用的天数和实际用的天数,但题目中只给出了实际用的天数y,没有给出计划用的天数,所以C选项是无法求出的。
D选项:照这样计算,这些水泥一共可以用多少天,可以通过$总水泥量 ÷ 每天用量 = \frac{x}{1.9}$来求得(结果向上取整,因为即使不够一天的量也需要一天来使用),所以D选项在理论上是可以求出的,只是需要一个向上取整的步骤。
答案:C。
4. 甲数是 a,比乙数的 2 倍多 8,表示乙数的式子是(
A.$2a-8$
B.$(a-8)÷2$
C.$(a+8)÷2$
D.$2a+8$
B
)。A.$2a-8$
B.$(a-8)÷2$
C.$(a+8)÷2$
D.$2a+8$
答案:
解析:本题可根据题目所给的数量关系,通过设未知数列出方程,进而求解表示乙数的式子。
步骤一:设未知数并列出方程
设乙数为$x$,已知甲数是$a$,且甲数比乙数的$2$倍多$8$,那么可得到等式:甲数$=$乙数$×2 + 8$,即$a = 2x + 8$。
步骤二:求解乙数$x$
为了得到表示乙数$x$的式子,需要对$a = 2x + 8$进行求解。
首先,方程两边同时减去$8$可得:$a - 8 = 2x + 8 - 8$,即$a - 8 = 2x$。
然后,方程两边同时除以$2$可得:$(a - 8)÷2 = 2x÷2$,即$x = (a - 8)÷2$。
答案:B
步骤一:设未知数并列出方程
设乙数为$x$,已知甲数是$a$,且甲数比乙数的$2$倍多$8$,那么可得到等式:甲数$=$乙数$×2 + 8$,即$a = 2x + 8$。
步骤二:求解乙数$x$
为了得到表示乙数$x$的式子,需要对$a = 2x + 8$进行求解。
首先,方程两边同时减去$8$可得:$a - 8 = 2x + 8 - 8$,即$a - 8 = 2x$。
然后,方程两边同时除以$2$可得:$(a - 8)÷2 = 2x÷2$,即$x = (a - 8)÷2$。
答案:B
5. 一个长方体的长、宽、高分别为 a 米,b 米、h 米,如果长、宽不变,高增加 2 米,长方体的体积增加(
A.$2ab$
B.$2abg$
C.$abh$
D.$2h$
2ab
)立方米。A.$2ab$
B.$2abg$
C.$abh$
D.$2h$
答案:
解析:
首先,我们需要知道长方体的体积公式,即体积 $V = 长 × 宽 × 高$。
原始长方体的体积为 $V_1 = a × b × h = abh$ 立方米。
当长方体的高增加2米时,新的高为 $h + 2$ 米,所以新的体积 $V_2 = a × b × (h + 2) = ab(h + 2)$ 立方米。
体积的增加量就是新的体积减去原始体积,即 $V_2 - V_1 = ab(h + 2) - abh = 2ab$ 立方米。
所以,长方体的体积增加了 $2ab$ 立方米。
答案:A
首先,我们需要知道长方体的体积公式,即体积 $V = 长 × 宽 × 高$。
原始长方体的体积为 $V_1 = a × b × h = abh$ 立方米。
当长方体的高增加2米时,新的高为 $h + 2$ 米,所以新的体积 $V_2 = a × b × (h + 2) = ab(h + 2)$ 立方米。
体积的增加量就是新的体积减去原始体积,即 $V_2 - V_1 = ab(h + 2) - abh = 2ab$ 立方米。
所以,长方体的体积增加了 $2ab$ 立方米。
答案:A
查看更多完整答案,请扫码查看


