《2025年名校优录小升初总复习六年级数学人教版》

四、计算下列图形的表面积和体积。
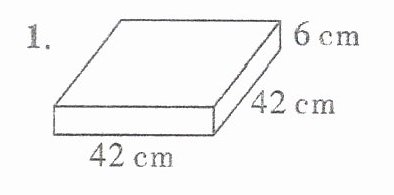
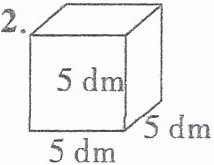
1.
2.

答案： 解析：本题主要考查长方体和正方体表面积与体积的计算。对于长方体，表面积公式为$S=(ab + ah + bh)×2$，体积公式为$V = abh$；对于正方体，表面积公式为$S = 6a^2$，体积公式为$V = a^3$。
答案：
1. 长方体的表面积：
$\;\;\;\;(42×42 + 42×6 + 42×6)×2$
$=(1764 + 252 + 252)×2$
$=(2016 + 252)×2$
$= 2268×2$
$= 4536$（$cm^2$）
长方体的体积：
$\;\;\;\;42×42×6$
$=1764×6$
$= 10584$（$cm^3$）
2. 正方体的表面积：
$\;\;\;\;5×5×6$
$=25×6$
$= 150$（$dm^2$）
正方体的体积：
$\;\;\;\;5×5×5$
$=25×5$
$= 125$（$dm^3$）

1.(长沙开福区)某种饮料罐的形状为圆柱形,底面直径是6 cm,高是12 cm,将24罐这种饮料按如图所示的方式放入箱内,这个箱子的长、宽、高至少是多少厘米?这个箱子的容积大约是多少?

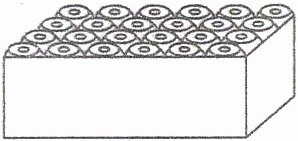
答案： 本题可根据饮料罐的排列方式以及圆柱的直径和高来确定箱子的长、宽、高，再根据长方体容积公式计算箱子的容积。
步骤一：分析箱子的长、宽、高
从图中可以看出，饮料罐是按一定规律放入箱内的。
箱子的长：饮料罐底面直径是$6cm$，箱子长的一边放了$6$罐饮料，那么箱子的长至少是$6$个饮料罐底面直径的长度，即$6×6 = 36$（$cm$）。
箱子的宽：箱子宽的一边放了$4$罐饮料，所以箱子的宽至少是$4$个饮料罐底面直径的长度，即$4×6 = 24$（$cm$）。
箱子的高：饮料罐的高是$12cm$，箱子要装下饮料罐，其高至少等于饮料罐的高，即$12cm$。
步骤二：计算箱子的容积
已知箱子的形状为长方体，根据长方体的容积公式$V = a×b×h$（其中$V$表示容积，$a$表示长，$b$表示宽，$h$表示高），把箱子的长$36cm$、宽$24cm$、高$12cm$代入公式可得：
$V = 36×24×12$
$= 864×12$
$= 10368$（$cm^3$）
综上，这个箱子的长至少是$36$厘米，宽至少是$24$厘米，高至少是$12$厘米，这个箱子的容积大约是$10368cm^3$。

2.一个容器(如下图)里原有0.36升的水,乌鸦叼多少立方厘米的石子放进容器里,就能喝到水?

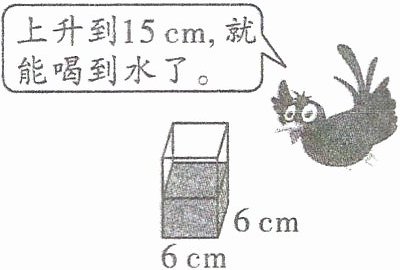
答案： 解析：本题考查长方体体积的计算方法，我们可根据放入石子后水上升的体积即为石子体积这一原理来求解。需要先统一单位，再计算出水面上升的高度，最后根据长方体体积公式求出石子体积。
答案：
解：$0.36$升$ = 360$立方厘米，$15$厘米$ = 15$厘米，$6$厘米$ = 6$厘米。
容器底面积为$6×6 = 36$（平方厘米）。
原有水$360$立方厘米，根据长方体体积公式$V = S× h$（$V$是体积，$S$是底面积，$h$是高），可得原来水的高度为$360÷36 = 10$（厘米）。
那么水面上升的高度为$15 - 10 = 5$（厘米）。
所以石子的体积为$36×5 = 180$（立方厘米）。
答：乌鸦叼$180$立方厘米的石子放进容器里，就能喝到水。

3.(湖南永州)用长10厘米、宽7厘米、高2厘米的6个同样的长方体物体拼凑成一个长方体包装物,怎样包装最节约包装纸?大约需要包装纸多少平方厘米?(6分)

答案： 解：要想最节约包装纸，就要把最大的面拼在一起。
长方体最大的面是长$×$宽的面，即$10×7$的面。
将$6$个长方体这样包装，新的长方体高为$2×6 = 12$厘米，长是$10$厘米，宽是$7$厘米。
根据长方体表面积公式$S=(ab + ah + bh)×2$（其中$a$为长，$b$为宽，$h$为高），可得：
$(10×7 + 10×12 + 7×12)×2$
$=(70 + 120 + 84)×2$
$=(190 + 84)×2$
$=274×2$
$=548$（平方厘米）
答：把$10×7$的面拼在一起最节约包装纸，大约需要包装纸$548$平方厘米。

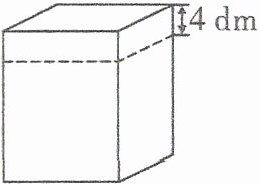
4.一块长方体木料(如图),从上面截下一块高为4 dm的长方体后,表面积减少了$240 dm^2,$剩下的木料为一个正方体。这块长方体木料原来的体积是多少立方分米?

答案： 解析：本题考查了长方体的表面积和体积的计算。
根据题意可知，把一个长方体从上面截下一块高为4分米的长方体后，表面积减少了$240$平方分米，表面积减少的是4个完全相同的直角长方形的面积，由此可以求出长方体的底面边长，$240÷ 4÷ 4=60÷ 4=15$（分米），
则剩下木料的边长为15分米，即原木料的宽和高都是15分米，
进而求出原木料的长是$15 + 4 = 19$（分米），
然后根据长方体的体积公式，$体积=长×宽×高$，把数据代入公式解答。
答案：$240÷ 4÷ 4=15(dm)$，
$15+4=19(dm)$，
$15× 15× 19=4275(dm^{3})$，
所以长方体木料原来的体积是$4275dm^{3}$。

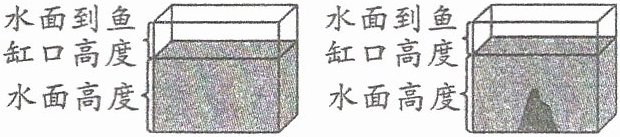
5.(河南开封)小芳家有一个无盖的长方体玻璃鱼缸,长8分米,宽3分米,高6分米。鱼缸里原来水面高度与水面到鱼缸口高度的比是2∶1,在鱼缸里放入一块景观石后,现在鱼缸里水面高度与水面到鱼缸口高度的比是7∶3。这块景观石的体积是多少立方分米?

答案： 解析：本题可先根据已知条件求出原来水面的高度，再求出放入景观石后水面的高度，最后根据长方体体积公式求出景观石的体积。
1. 求出原来水面的高度：
已知鱼缸里原来水面高度与水面到鱼缸口高度的比是$2:1$，那么原来水面高度占鱼缸高度的$\frac{2}{2 + 1}=\frac{2}{3}$。
因为鱼缸高$6$分米，所以原来水面高度为$6×\frac{2}{3}=4$（分米）。
2. 求出放入景观石后水面的高度：
已知放入一块景观石后，现在鱼缸里水面高度与水面到鱼缸口高度的比是$7:3$，那么现在水面高度占鱼缸高度的$\frac{7}{7 + 3}=\frac{7}{10}$。
所以现在水面高度为$6×\frac{7}{10}=4.2$（分米）。
3. 求出景观石的体积：
放入景观石后水面上升的体积就是景观石的体积。
水面上升的高度为$4.2 - 4 = 0.2$（分米）。
已知鱼缸长$8$分米，宽$3$分米，根据长方体体积公式$V = a× b× h$（其中$V$为体积，$a$为长，$b$为宽，$h$为高），可得景观石的体积为：
$8×3×0.2 = 4.8$（立方分米）。
答案：
现在水面高度：$6×\frac{7}{7 + 3}=4.2$（分米）
原来水面高度：$6×\frac{2}{2 + 1}=4$（分米）
水面上升高度：$4.2 - 4 = 0.2$（分米）
景观石体积：$8×3×0.2 = 4.8$（立方分米）
答：这块景观石的体积是$4.8$立方分米。