第3页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
16.[情境题](2024·烟台)目前全球最薄的手撕钢产自中国,厚度只有0.015毫米,约是A4纸厚度的六分之一.已知1毫米=1百万纳米,0.015毫米等于多少纳米?将结果用科学记数法表示为 ( )
[A]0.15×10³纳米 [B]1.5×10⁴纳米
[C]15×10⁻⁵纳米 [D]1.5×10⁻⁶纳米
[A]0.15×10³纳米 [B]1.5×10⁴纳米
[C]15×10⁻⁵纳米 [D]1.5×10⁻⁶纳米
答案:
B [由题意可得 1 毫米 = 1 百万纳米$ = 10^6 $纳米,则 0.015 毫米$ = 1.5×10^(-2)×10^6 $纳米$ = 1.5×10^4 $纳米. 故选 B.]
17.(2024·内蒙古包头)若m,n互为倒数,且满足m+mn=3,则n的值为 ( )
[A]$\frac{1}{4}$ [B]$\frac{1}{2}$ [C]2 [D]4
[A]$\frac{1}{4}$ [B]$\frac{1}{2}$ [C]2 [D]4
答案:
B [
∵m,n 互为倒数,
∴m·n = 1,
∵m + mn = 3,
∴m = 2,则 n = 1/2. 故选 B.]
∵m,n 互为倒数,
∴m·n = 1,
∵m + mn = 3,
∴m = 2,则 n = 1/2. 故选 B.]
18.(2024·菏泽二模)点M,N在数轴上的位置如图所示,其对应的数分别是m和n.对于以下结论:
①n-m>0;②mn>0;③|m|>|n|;④-m>n.其中正确的个数是 ( )
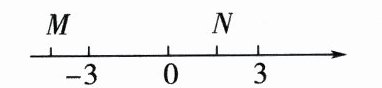
[A]1 [B]2 [C]3 [D]4
①n-m>0;②mn>0;③|m|>|n|;④-m>n.其中正确的个数是 ( )
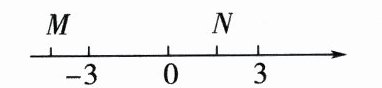
[A]1 [B]2 [C]3 [D]4
答案:
C [由数轴知 m < 0 < n,|m| > |n|,
∴n - m > 0,mn < 0, -m > n,
∴①③④正确. 故选 C.]
∴n - m > 0,mn < 0, -m > n,
∴①③④正确. 故选 C.]
19.(2024·陕西)小华探究“幻方”时,提出了一个问题:
如图,将0,-2,-1,1,2这五个数分别填在五个小

正方形内,使横向三个数之和与纵向三个数之和相等,则填入中间位置的小正方形内的数可以是________.(写出一个符合题意的数即可)
如图,将0,-2,-1,1,2这五个数分别填在五个小

正方形内,使横向三个数之和与纵向三个数之和相等,则填入中间位置的小正方形内的数可以是________.(写出一个符合题意的数即可)
答案:
0(答案不唯一) [由题意,填写如下 1 + 0 + (-1) = 0,2 + 0 + (-2) = 0,满足题意(答案不唯一).]
1 + 0 + (-1) = 0,2 + 0 + (-2) = 0,满足题意(答案不唯一).]
0(答案不唯一) [由题意,填写如下
 1 + 0 + (-1) = 0,2 + 0 + (-2) = 0,满足题意(答案不唯一).]
1 + 0 + (-1) = 0,2 + 0 + (-2) = 0,满足题意(答案不唯一).] 20.(2024·四川成都)若m,n为实数,且(m+4)²+$\sqrt{n - 5}$=0,则(m+n)²的值为________.
答案:
1 [
∵$(m + 4)^2 + √(n - 5) = 0,$
∴m + 4 = 0,n - 5 = 0,解得 m = -4,n = 5,
∴$(m + n)^2 = (-4 + 5)^2 = 1,$故答案为 1.]
∵$(m + 4)^2 + √(n - 5) = 0,$
∴m + 4 = 0,n - 5 = 0,解得 m = -4,n = 5,
∴$(m + n)^2 = (-4 + 5)^2 = 1,$故答案为 1.]
21.(8分)(2024·眉山)计算:($\sqrt{3}$-π)⁰+(-$\frac{1}{2}$)⁻²+2sin45°-|1-$\sqrt{2}$|.
答案:
解:$(√3 - π)^0 + (-1/2)^(-2) + 2sin 45° - |1 - √2| = 1 + 4 + 2×√2/2 - (√2 - 1) = 1 + 4 + √2 - √2 + 1 = 6.$
22.[新定义]定义一种新运算:对于两个非零实数a,b,a※b=$\frac{x}{a}$+$\frac{y}{b}$.若2※(-2)=1,则(-3)※3的值是________.
答案:
-2/3 [
∵2※(-2) = 1,
∴x/2 + y/(-2) = 1,
∴x - y = 2.
∴(-3)※3 = x/(-3) + y/3 = -1/3(x - y) = -1/3×2 = -2/3.]
∵2※(-2) = 1,
∴x/2 + y/(-2) = 1,
∴x - y = 2.
∴(-3)※3 = x/(-3) + y/3 = -1/3(x - y) = -1/3×2 = -2/3.]
查看更多完整答案,请扫码查看


