《2025年初中总复习山东教育出版社数学中考》

11.(2024·兖州区一模)如图,在正方形ABCD中,点E,F分别是AB,CD的中点,AF,DE相交于点M,G为BC上一点,N为EG的中点.若BG=6,CG=2,则线段MN的长度为　(　　)
[A]$\sqrt{17}$　　　[B]$\sqrt{5}$　　　　　[C]2　　　　　　[D]$\sqrt{13}$
　　　　　　　　　　　　　　　　　　　　　　

答案：
A　[如图所示,连接EF,DG,
　
∵在正方形ABCD中,AB//CD,AB=CD,∠BAD=90°,
　　又
∵E,F分别为边AB,CD的中点，
　　　　　　　　　　　　　　　　　　　　
∴AE=DF,AE//DF,
∴四边形AEFD为平行四边形，
∴四边形AEFD为矩形，
∴AF=ED,
∴M为AF,ED的中点，
　又
∵N为EG的中点,
∴在△EGD中,MN//DG,MN=$\frac{1}{2}$DG.
　在Rt△DCG中,利用勾股定理，求得DG=2$\sqrt{17}$,
　则MN= $\sqrt{17}$.故选A.]

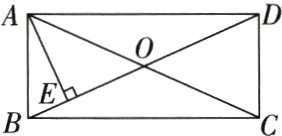
12.(2024·东昌府区二模)如图,在矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,若BE=2,则矩形ABCD的面积为__________.
　　　　　　　　　　　　　　　　　　　　　　

答案： 16$\sqrt{3}$　[在矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,BE=2,
∴∠BAD=90°,
∴90°=∠BAD=∠BAE+∠DAE=∠BAE+2∠BAE,
∴∠BAE=30°,
∵AE⊥BD,即∠AEB=90°,
∴∠ABE=90°−∠BAE=90°−30°=60°,
　在Rt△ABE中,$AB=\frac{BE}{\cos∠ABE}=\frac{2}{\cos 60°}=\frac{2}{\frac{1}{2}}=4$,
　在Rt△ABD中,AD=AB·$\tan∠ABE=4×\tan 60°=4\sqrt{3}$,
∴$S_{矩形ABCD}=AB·AD=4×4\sqrt{3}=16\sqrt{3}$.

13.(12分)[项目式学习试题](2024·泰安)综合与实践
为了研究折纸过程蕴含的数学知识,某校九年级数学兴趣小组的同学进行了数学折纸探究活动.
【探究发现】(1)同学们对一张矩形纸片进行折叠，如图1,把矩形纸片ABCD翻折,使矩形顶点B的对应点G恰好落在矩形的一边CD上,折痕为EF,将纸片展平,连接BG,EF与BG相交于点H.同学们发现图形中四条线段成比例,即$\frac{EF}{BG}$=$\frac{AB}{BC}$,请你判断同学们的发现是否正确，并说明理由.
【拓展延伸】(2)同学们对老师给出的一张平行四边形纸片进行研究,如图2,BD是平行四边形纸片ABCD的一条对角线,同学们将该平行四边形纸片翻折,使点A的对应点G,点C的对应点H都落在对角线BD上,折痕分别是BE和DF.将纸片展平,连接EG,FH,FG.同学们探究后发现,若FG//CD,那么点G恰好是对角线BD的一个“黄金分割点”,即BG²=BD·GD.请你判断同学们的发现是否正确,并说明理由.
　　　　　　　　　　　　

答案：
解:
(1)$\frac{EF}{BG}=\frac{AB}{BC}$正确，理由如下:
　作EM⊥BC,垂足为点M.
　　　　　　　　　　　　　　　　　
∵EF⊥BG,
∴∠BFH=90°,
∴∠FBH+∠BFH=90°,
∵∠EMF=90°,
∴∠MEF+∠MFE=90°,
∴∠FBH=∠MEF.
　又
∵∠EMF=∠C=90°,
∴△EMF∽△BCG.
∴$\frac{EF}{BG}=\frac{EM}{BC}$.
∵四边形ABCD是矩形,EM⊥BC,
∴四边形ABME是矩形.
∴AB=EM,
∴$\frac{EF}{BG}=\frac{AB}{BC}$.
(2)同学们的发现正确，理由如下:
∵CD//FG,
∴$\frac{CD}{FG}=\frac{BD}{BG}$,∠CDF=∠DFG,
　由折叠的性质可知∠CDF=∠BDF,
∴∠DFG=∠BDF,
∴GD=GF,
∴$\frac{CD}{GD}=\frac{BD}{BG}$.
　由平行四边形及折叠的性质可知AB=BG,AB=CD,
∴$\frac{BG}{GD}=\frac{BD}{BG}$,
∴$BG^{2}=BD·GD$.
　即点G为BD的一个黄金分割点.