《2025年学习之友八年级数学下册北师大版》

1.下列三角形：① 有两个角等于$60^{\circ}$；② 有一个角等于$60^{\circ}$的等腰三角形；③ 三个外角（每个顶点处各取一个外角）都相等的三角形；④ 一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有 （ ）
A. ①②③
B. ①②④
C. ①③
D. ①②③④

答案： D

2.将一副三角尺按如图所示的方式叠放在一起，若$AB = 16\mathrm{cm}$，则阴影部分的面积是 __________$\mathrm{cm}^{2}$.

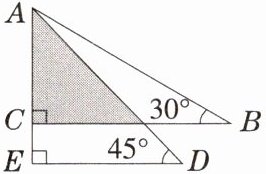
答案： 32

3.若三角形中最小角是$60^{\circ}$，则这个三角形是 ____________ 三角形.

答案： 等边

4.在$\mathrm{Rt}\triangle ABC$中，$CD$，$CE$分别是斜边$AB$上的高和中线，如果$\angle A = 30^{\circ}$，$BD = 1\mathrm{cm}$，那么$\angle BCD = $__________，$BC = $__________$\mathrm{cm}$，$AD = $__________$\mathrm{cm}$.

答案： $30^{\circ}$@@2@@$3\cdots\cdots$

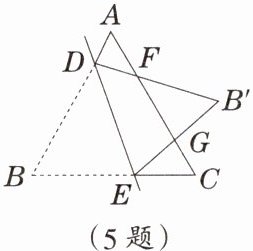
5.已知等边$\triangle ABC$中，点$D$，$E$分别在边$AB$，$BC$上，把$\triangle BDE$沿直线$DE$翻折，使点$B$落在点$B'$处，$DB'$，$EB'$分别交边$AC$于点$F$，$G$，若$\angle ADF = 80^{\circ}$，则$\angle EGC$的度数为 __________.

答案： $80^{\circ}$

6.已知$\triangle ABC$为等边三角形且$AD\perp BC$于$D$，以$AD$为一边作$\triangle ADE$，且$DE\perp AC$，$\angle CAE = 30^{\circ}$. 求证：$\triangle ADE$为等边三角形.

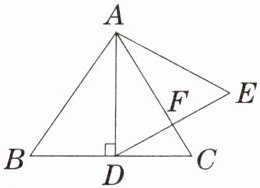
答案： 证明：$\because\triangle ABC$为等边三角形（已知） $AD\perp BC$ $\therefore\angle BAD = \angle CAD = 30^{\circ}$ $\because\angle CAE = 30^{\circ}$（已知） $\therefore\angle DAE=\angle DAC+\angle CAE = 60^{\circ}$ $\because DE\perp AC$（已知） $\therefore\angle ADE = 90^{\circ}-\angle DAC = 60^{\circ}$ $\therefore\angle AED = 180^{\circ}-\angle DAE-\angle ADE = 60^{\circ}$ $\therefore\triangle ADE$为等边三角形.

1.$\triangle ABC$的三个内角的度数为$\alpha$，$\beta$，$\gamma$，满足$\begin{cases}\alpha+\beta = 120^{\circ},\\2\alpha-\beta = 60^{\circ},\end{cases}$则$\triangle ABC$为 （ ）
A. 直角三角形
B. 等腰直角三角形
C. 等腰三角形
D. 等边三角形

答案： D

2.等边三角形的边长为$2$，则该三角形的面积是 （ ）
A. $4\sqrt{3}$
B. $2\sqrt{3}$
C. $\sqrt{3}$
D. $3$

答案： C

3.命题“如果一个三角形的一条边长等于另一条边长的一半，那么这条边所对的角等于$30^{\circ}$”是 ________（填“真”或“假”）命题.

答案： 假

4.某人要测一古塔$AB$的高度，他采用了如下方法：沿直线$CB$向塔基前进，在$C$处测得$\angle C = 15^{\circ}$，在$D$处测得$\angle ADB = 30^{\circ}$，若$CD = 80\mathrm{m}$，则塔高$AB$等于 __________$\mathrm{m}$.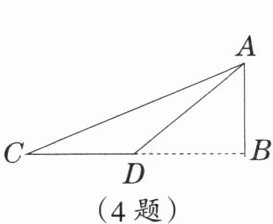

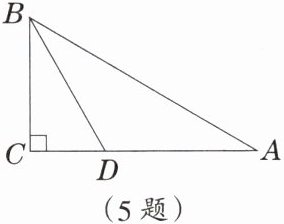
答案： 40