《2025年学习之友八年级数学下册北师大版》

8.对于不等式“$5x + 4y\leqslant20$”，我们可以这样解释：香蕉每千克5元，苹果每千克4元，购买$x$千克香蕉与$y$千克苹果的总金额不超过20元.
请你结合生活实际，设计具体情境表示下列不等式.
（1）$3x - 1\geqslant5$；
（2）$4a + 3b<8$.

答案： 可理解为：现有 3 个房间，每个房间住$x$人，但有一间空余一床位，住宿总人数不少于 5 人.@@可理解为：长为$2a$ cm，宽为$\frac{3}{2}b$ cm 的长方形，其周长小于 8 cm.

9.物美超市准备用甲、乙两种糖配制50千克什锦糖，其中，甲种糖价格是24元 / 千克，乙种糖价格是18元 / 千克，如果要使价格不高于21元 / 千克，则掺入甲种糖的质量$x$应满足的关系式是 ____________________.

答案： $24x + 18(50 - x) \leq 21\times50$

10.比较大小.（在横线上填“>”“<”或“=”）
（1）$4^{2}+3^{2}\underline{\qquad}2\times4\times3$；
（2）$(-2)^{2}+1^{2}\underline{\qquad}2\times(-2)\times1$；
（3）$(\sqrt{2})^{2}+(\frac{1}{2})^{2}\underline{\qquad}2\times\sqrt{2}\times\frac{1}{2}$；
（4）$2^{2}+2^{2}\underline{\qquad}2\times2\times2$；
……
通过观察归纳，请你写出反映这种规律的一般结论.

答案： >@@>@@>@@=@@$a^2 + b^2 \geq 2ab$ 当$a = b$时，等号成立.

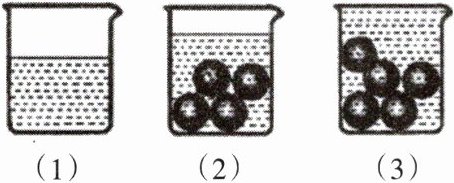
1.下图是测量一颗玻璃球体积的过程：
（1）将300 mL的水倒进一个容量为500 mL的量杯中；
（2）将四颗相同体积的玻璃球放入水中，结果水没有满；
（3）再加一颗同样体积的玻璃球放入水中，结果水满溢出.
根据以上过程，推测这样一颗玻璃球的体积在 ______$cm^{3}$以上，______$cm^{3}$以下.

答案： 40@@50

2.某商店将平板电视先按原价提高40%，然后在广告中写上“大酬宾，八折优惠”. 结果每台平板电视比按原价销售多赚240元以上. 试问平板电视原价在多少元以上？设平板电视原价为$x$元，用关于$x$的不等式表示题目中的不等关系. 如果平板电视原价是2200元，那么它是否符合要求？

答案： $80\%(1 + 40\%)x - x > 240$

1.用“＞”或者“＜”填空，并写明理由.
（1）若$-x<1$，则$x$ ＞ $-1$，理由是 不等式两边同时乘（或除以）同一个负数，不等号的方向改变.
（2）若$\frac{a}{6}<-\frac{b}{3}$，则$a$ ＜ $-2b$，理由是 不等式两边同时乘（或除以）同一个正数，不等号的方向不变.
（3）若$m - 2>n - 2$，则$m$ ＞ $n$，理由是 不等式两边同时加（或减）同一个数或式子，不等号的方向不变.

答案： >@@不等式的两边都乘(或除以)同一个负数，不等号的方向改变@@<@@不等式的两边都乘(或除以)同一个正数，不等号的方向不变@@>@@不等式的两边都加(或减)同一个整式，不等号的方向不变