第77页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
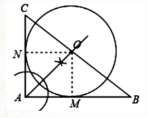
3. 如图,在$\triangle ABC$中,$\angle A= 90^{\circ}$.
(1)请你画一个半圆使得圆心O在边BC上,并与AB、AC都相切(保留画图痕迹);
(2)已知$AB= 4,AC= 3$,求(1)中所画圆的半径.
]

(1)请你画一个半圆使得圆心O在边BC上,并与AB、AC都相切(保留画图痕迹);
(2)已知$AB= 4,AC= 3$,求(1)中所画圆的半径.
]

答案:
解:连接圆心和两个切点M和N
则四边形OMAN是正方形
设半径为r
∴CN=AC-AN=3-r,BM= AB-AM=4-r
∴$OC=\sqrt{CN^2+ON^2},$$OB=\sqrt{BM^2+OM^2}$
∴$BC=OC+OB=\sqrt{(3-r)^2+r^2}+\sqrt{r^2+(4-r)^2}=\sqrt{3^2+4^2}$
解得$r=\frac {12}7$
解:连接圆心和两个切点M和N
则四边形OMAN是正方形
设半径为r
∴CN=AC-AN=3-r,BM= AB-AM=4-r
∴$OC=\sqrt{CN^2+ON^2},$$OB=\sqrt{BM^2+OM^2}$
∴$BC=OC+OB=\sqrt{(3-r)^2+r^2}+\sqrt{r^2+(4-r)^2}=\sqrt{3^2+4^2}$
解得$r=\frac {12}7$

4. 为检测生产的一种铁球的大小是否符合要求,工人设计了一个工件槽,工件槽的两个底角均为$90^{\circ}$,尺寸如图所示(单位:cm).将形状规则的铁球放入槽内,若同时具有图中的A、B、E三个接触点,则该球大小符合要求.请结合图中数据,计算符合要求的铁球直径.
]

]

答案:
解:如图,对点O、C、 D作标注,连接OA,设OE交AB于点P
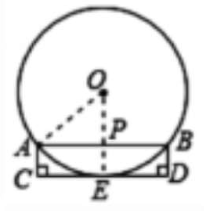
∵AC⊥CD , BD⊥CD , AC//BD
∴四边形ABDC为矩形
∴AB=CD=16cm , AB//CD
∵CD与圆O相切
∴OE⊥ CD
∵AB//CD , OE⊥CD
∴OE ⊥ AB
∴$ AP= BP=\frac 12AB= 8cm$
∵OE⊥CD ,四边形ABDC为矩形
∴EP= BD= 4cm
设铁球的半径为rcm ,即OA=OE=rcm ,则OP=(r-4)cm
∵△OAP为直角三角形
∴$OA^2=OP^2+AP^2$
∴$r^2 =(r-4)^2+8^2$
∴r=10
∴铁球的直径为20cm
解:如图,对点O、C、 D作标注,连接OA,设OE交AB于点P

∵AC⊥CD , BD⊥CD , AC//BD
∴四边形ABDC为矩形
∴AB=CD=16cm , AB//CD
∵CD与圆O相切
∴OE⊥ CD
∵AB//CD , OE⊥CD
∴OE ⊥ AB
∴$ AP= BP=\frac 12AB= 8cm$
∵OE⊥CD ,四边形ABDC为矩形
∴EP= BD= 4cm
设铁球的半径为rcm ,即OA=OE=rcm ,则OP=(r-4)cm
∵△OAP为直角三角形
∴$OA^2=OP^2+AP^2$
∴$r^2 =(r-4)^2+8^2$
∴r=10
∴铁球的直径为20cm
5. 如图,在正方形ABCD中,点O在对角线AC上,以点O为圆心,OA的长为半径的$\odot O$与BC相切于点M,与AB、AD分别相交于点E、F.
(1)求证:CD是$\odot O$的切线;
(2)已知正方形ABCD的边长为1,求$\odot O$的半径.
]

(1)求证:CD是$\odot O$的切线;
(2)已知正方形ABCD的边长为1,求$\odot O$的半径.
]

答案:
(1)证明:连接OM,过点O作ON⊥CD ,垂足为N
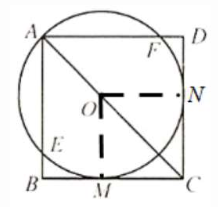
∵圆O与BC相切于M
∴OM⊥BC,
∵正方形ABCD中, AC平分∠BCD
又
∵ON⊥CD , OM⊥BC
∴OM = ON
∴CD与圆O相切
(2)设圆O的半径为R ,则OM = R
∵正方形ABCD的边长为1,
∴$ AC=\sqrt2,$$ OC=\sqrt2- R$
在Rt△OMC中,∠OCM=45°
∴CM=OM=R
∴$ R^2+ R^2=(\sqrt2- R)^2$
解得$R=2-\sqrt2$
(1)证明:连接OM,过点O作ON⊥CD ,垂足为N

∵圆O与BC相切于M
∴OM⊥BC,
∵正方形ABCD中, AC平分∠BCD
又
∵ON⊥CD , OM⊥BC
∴OM = ON
∴CD与圆O相切
(2)设圆O的半径为R ,则OM = R
∵正方形ABCD的边长为1,
∴$ AC=\sqrt2,$$ OC=\sqrt2- R$
在Rt△OMC中,∠OCM=45°
∴CM=OM=R
∴$ R^2+ R^2=(\sqrt2- R)^2$
解得$R=2-\sqrt2$
6. 如图①、②、③、…、ⓝ,在$\odot O$的内接正三角形ABC、正四边形ABCD、正五边形ABCDE、…、正n边形$ABCDE…$中,点M、N分别在边AB、BC上,且$BM= CN$,连接OM、ON.

(1)图①中的$\angle O= $______°;
(2)图②中的$\angle O= $______°,图③中的$\angle O= $______°;
(3)试探究$\angle O$的度数与正n边形的边数n之间的关系(直接写出答案).

(1)图①中的$\angle O= $______°;
(2)图②中的$\angle O= $______°,图③中的$\angle O= $______°;
(3)试探究$\angle O$的度数与正n边形的边数n之间的关系(直接写出答案).
答案:
120
90
72
120
90
72
查看更多完整答案,请扫码查看


