《2024年学习与评价江苏教育出版社九年级数学上册苏科版》

如何在操场上画一个半径为6m的圆？说说你的做法和理由.

答案： 如将长为6 m的绳子一端点O固定，另一端绑上粉笔绕着点O在平面内旋转1圈，即得半径为6 m的圆
理由:到点O的距离等于6 m的点的集合是以点O为圆心，6 m为半径的圆

例1 已知$\odot O$的半径为4cm,A是线段OP的中点,当$OP= 6\ cm$时,点A在$\odot O$______；当$OP= 8\ cm$时,点A在$\odot O$______；当$OP= 10\ cm$时,点A在$\odot O$______.
分析 判断点和圆的位置关系,就需要比较“点到圆心的距离d”与“圆的半径r”的大小.当$d\lt r$时,点在圆内；当$d= r$时,点在圆上；当$d\gt r$时,点在圆外.
解 当$OP= 6\ cm$时,$OA= 3\ cm\lt4\ cm$,所以点A在$\odot O$内；
当$OP= 8\ cm$时,$OA= 4\ cm$,所以点A在$\odot O$上；
当$OP= 10\ cm$时,$OA= 5\ cm\gt4\ cm$,所以点A在$\odot O$外.

答案： 内
上
外

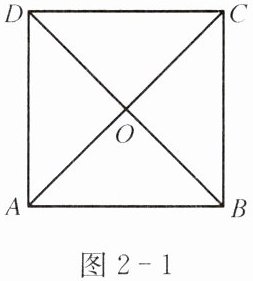
例2 如图2-1,正方形ABCD的对角线AC、BD相交于点O.
求证：A、B、C、D四个点在以点O为圆心的同一个圆上.
分析 判断几个点是否在同一个圆上,关键是看这几个点到某一个点的距离是否相等.
证明 $\because$ 四边形ABCD是正方形,
$\therefore OA= OC= \frac{1}{2}AC$,$OB= OD= \frac{1}{2}BD$,$AC= BD$.
$\therefore OA= OC= OB= OD$.
$\therefore$ A、B、C、D四个点在以点O为圆心,OA为半径的圆上.
思考 若四边形是矩形,则上述结论还成立吗？为什么？

答案： 解：上述结论还成立
因为矩形的对角线相等，则OA=OB=OC=OD仍然成立

1. 填空题：
(1)已知$\odot A$的直径为8cm,且点B在$\odot A$上,那么$AB= $______cm；
(2)已知$\odot O$的半径是3cm,且$OP= 2\ cm$,$OQ= 3\ cm$,则点P、Q与$\odot O$的位置关系是：点P在$\odot O$______,点Q在$\odot O$______；
(3)正方形ABCD的边长为1cm,对角线AC、BD相交于点O,以点A为圆心,1cm长为半径画圆,则点B、C、D、O与$\odot A$的位置关系为：点B在$\odot A$______,点C在$\odot A$______,点D在$\odot A$______,点O在$\odot A$______.

答案： 4
内
上
上
外
上
内