《2024年学习与评价江苏教育出版社九年级数学上册苏科版》

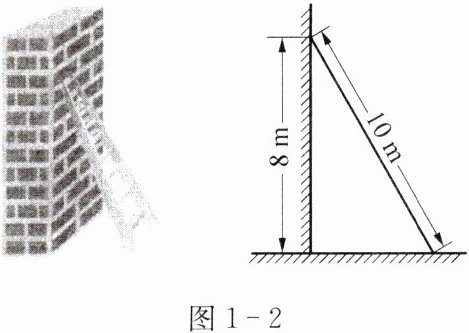
如图1-2,长为10 m的梯子斜靠在墙上,梯子的顶端与地面的距离为8 m.如果梯子顶端下滑1 m,那么梯子的底端滑动了多少米?

答案： 解：设梯子的底端滑动了x米
$ (x+6)^2+7^{2}=10^{2}$
解得$x_1=-6+\sqrt{51}，$$x_2=-6-\sqrt{51}($不合题意，舍去)
答：梯子的底端滑动了$(-6+\sqrt{51})$米。

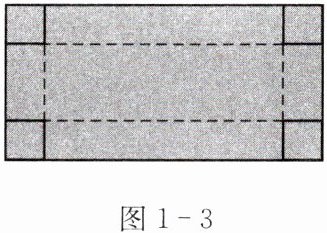
例 如图1-3,一块矩形铁皮的长是宽的2倍,四角各截去一个正方形,制成高是5 cm、容积是$500 cm^3$的无盖长方体容器.求这块铁皮的长和宽.
分析 设这块铁皮的宽是x cm,则制成的长方体容器底面的宽是(x-10)cm,长是(2x-10)cm,根据“长×宽×高= 长方体容积”,列出方程.
解 设这块铁皮的宽是x cm.
根据题意,得
5(x-10)(2x-10)= 500,
即
$x^2-15x= 0.$

解方程,得
$x_1= 15,x_2= 0($不合题意,舍去).
所以
x= 15,2x= 30.
答 这块铁皮的长是30 cm,宽是15 cm.

答案：