《2024年学习与评价江苏教育出版社九年级数学上册苏科版》

3. 如图,圆锥的高为$\sqrt{3}$,底面半径为1,求圆锥侧面展开图的面积.

答案： 解：
∵ 圆锥的高为$\sqrt{3} ，$底面半径为1
圆锥的母线长为：$ \sqrt{(\sqrt{3})^2+1^{2}}=2$
圆锥的侧面展开图的面积为： π×2×1 = 2π

4. 如图,一只虫子从圆柱上点A处绕圆柱爬一圈到点B处.圆柱的高为6 cm,圆柱底面圆的周长为8 cm,求虫子爬行的最短路程.

答案： 解：最短路程为$ \sqrt{8^{2}+6^{2}}=10(\ \mathrm {cm})$

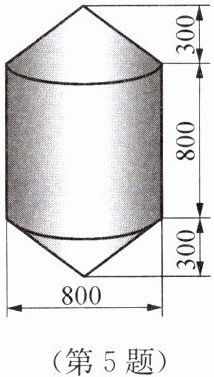
5. 锚标浮筒在打捞作业中用来标记锚或沉船位置.如图,它的上下两部分是圆锥,中间是一个圆柱(单位：mm).锚标浮筒需要在表面镀一层锌,电镀时每平方米用锌0.11 kg,要电镀100个这样的锚标浮筒,需要多少锌(精确到0.01 kg)？

答案： 解: 800mm=0.8m     300mm=0.3m
底面半径为0.8÷ 2=0.4(m )
圆锥的母线长为$\sqrt{0.4^2 + 0.3^2} = 0.5(m )$
一个圆锥的侧面积为$S=π×0.4×0.5=0.2π(m^2 )$
圆柱的侧面积为$2×π×0.4×0.8=0.64π(m^2 )$
浮筒的表面积为$2×0.2π+ 0.64π= 1.04π(m^2)$
需要用锌0.11× 1.04π× 100≈35.92(kg)
答：大约需要用锌35.92kg。

6. 如图,把半径为1的圆形纸片的四分之三沿半径OA剪开,依次用得到的半圆形纸片和四分之一圆形纸片做成两个圆锥的侧面.求这两个圆锥的底面积之比.

答案： 解：由题意知，小扇形的弧长为$ \frac 12π ，$则它组成的圆锥的底面半径为$ \frac 14，$
小圆锥的底面面积$ \frac 1{16}π$
大扇形的弧长为π ，则它组成的圆锥的底面半径为$ \frac 12，$
大圆锥的底面面积为$ \frac 14π$
∴大圆锥的底面面积：小圆锥的底面面积$= (\frac 14π)$：$(\frac 1{16}π)=4$：1