《2025年教材帮高中数学选择性必修第三册人教B版》

例 4 设随机变量$\xi$ 服从标准正态分布，则 $P(|\xi|\lt1.88)$ 等于（已知 $\varPhi(1.88)=0.97$）（D）

A.$0.03$
B.$0.06$
C.$0.97$
D.$0.94$

答案： 解析 $\because\varPhi(1.88)=0.97$，
$\therefore P(\xi\lt1.88)=0.97,P(\xi\geqslant1.88)=0.03$，
$\because$ 标准正态曲线关于直线 $x = 0$ 对称，
$\therefore P(\xi\geqslant1.88)+P(\xi\leqslant - 1.88)=0.03 + 0.03 = 0.06$，
故 $P(|\xi|\lt1.88)=1 - 0.06 = 0.94$.
答案 D

例 5 [多选题] (2025·湖南省邵阳市期中)
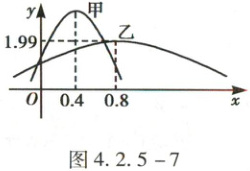
甲、乙两类水果的质量(单位：$kg$)分别服从正态分布 $N(\mu_1,\sigma_1^2),N(\mu_2,\sigma_2^2)$，正态曲线如图 4.2.5 - 7 所示，则下列说法正确的是(ABC)

A.甲类水果的平均质量 $\mu_1 = 0.4kg$
B.甲类水果的质量比乙类水果的质量更集中于平均质量
C.甲类水果的平均质量比乙类水果的平均质量小
D.乙类水果的质量服从的正态分布的参数 $\sigma_2 = 1.99$

答案： 解析 由图象可知甲曲线关于直线 $x = 0.4$ 对称，乙曲线关于直线 $x = 0.8$ 对称，$\therefore\mu_1 = 0.4,\mu_2 = 0.8$，故 A，C 正确；
$\because$ 甲曲线比乙曲线更“高瘦”，$\therefore$ 甲类水果的质量比乙类水果的质量更集中于平均质量，故 B 正确；
$\because$ 乙曲线的峰值为 $1.99$，即 $\frac{1}{\sigma_2\sqrt{2\pi}} = 1.99$，
$\therefore\sigma_2\neq1.99$，故 D 错误.
答案 ABC

例 6 [多选题] (2025·江苏省苏州市测试)
“杂交水稻之父”袁隆平一生致力于杂交水稻技术的研究、应用与推广，发明了“三系法”籼型杂交水稻，成功研究出“两系法”杂交水稻，创建了超级杂交稻技术体系，为我国粮食安全、农业科学发展和世界粮食供给做出了杰出贡献.某杂交水稻种植研究所调查某地水稻的株高，得出株高(单位：$cm$)服从正态分布，其正态密度函数为 $f(x)=\frac{1}{10\sqrt{2\pi}}· e^{-\frac{(x - 100)^2}{200}},x\in\mathbf{R}$，则下列说法正确的是(AC)

A.该地水稻的平均株高为 $100cm$
B.该地水稻株高的方差为 $10\sqrt{2}$
C.随机测量一株水稻，其株高在 $120cm$ 以上的概率比株高在 $70cm$ 以下的概率大
D.随机测量一株水稻，其株高在 $(80,90)$ 和在 $(100,110)$(单位：$cm$)的概率一样大

答案： 解析 由 $f(x)=\frac{1}{10\sqrt{2\pi}}e^{-\frac{(x - 100)^2}{200}}$，得 $\mu = 100,\sigma^2 = 100$，故该地水稻的平均株高为 $100cm$，该地水稻株高的方差为 $100$，故 A 正确，B 错误；
$P(x\gt120)=P(x\lt80)\gt P(x\lt70)$，所以随机测量一株水稻，其株高在 $120cm$ 以上的概率比株高在 $70cm$ 以下的概率大，故 C 正确；
根据正态曲线对称性知，$P(100\lt x\lt110)=P(90\lt x\lt100)\gt P(80\lt x\lt90)$，故随机测量一株水稻，其株高在 $(80,90)$ 和在 $(100,110)$(单位：$cm$)的概率不一样大，故 D 错误.
答案 AC