《2025年教材帮高中数学选择性必修第三册人教B版》

3. （2025·天津市和平区期末）某班组织知识竞赛，共有10道题目，现随机抽取3道让甲回答，规定至少要答对其中2道才能通过初试，已知甲只能答对其中6道，试求：
（1）随机抽出的3道题目甲能答对的道数的分布列；
（2）甲能通过初试的概率。

答案： 3.
(1)设随机抽出的3道题目甲能答对的道数为$X$，$X$的所有可能取值为$0,1,2,3$，易知$X$服从超几何分布，
则$P(X = 0) =\frac{C_{6}^{0}C_{4}^{3}}{C_{10}^{3}} = \frac{1}{30}$，$P(X = 1) =\frac{C_{6}^{1}C_{4}^{2}}{C_{10}^{3}} = \frac{3}{10}$，
$P(X = 2) =\frac{C_{6}^{2}C_{4}^{1}}{C_{10}^{3}} = \frac{1}{2}$，$P(X = 3) =\frac{C_{6}^{3}C_{4}^{0}}{C_{10}^{3}} = \frac{1}{6}$，
所以$X$的分布列为
$\begin{array}{c|cccc}X & 0 & 1 & 2 & 3 \\ \hline P &\frac{1}{30} &\frac{3}{10} &\frac{1}{2} &\frac{1}{6} \\ \end{array}$
(2)由至少要答对其中2道才能通过初试，可知$P(X\geq2) =$
$P(X = 2) + P(X = 3) = \frac{1}{2} + \frac{1}{6} = \frac{2}{3}$，
即甲能通过初试的概率为$\frac{2}{3}$。

例12 （2025·江西省宜春市丰城中学期中）树立和践行“绿水青山就是金山银山，坚持人与自然和谐共生”的理念越来越深入人心，已形成了全民自觉参与，造福百姓的良性循环。据此，某网站开展了关于生态文明建设进展情况的调查，调查数据表明，环境治理和保护问题仍是百姓最为关心的热点，参与调查者中关注此问题的约占80%。现从参与关注生态文明建设的调查者中随机选出200人，并将这200人按年龄分组：第1组$[15,25)$，第2组$[25,35)$，第3组$[35,45)$，第4组$[45,55)$，第5组$[55,65)$。由调查数据得到的频率分布直方图如图4.2.3-2所示。

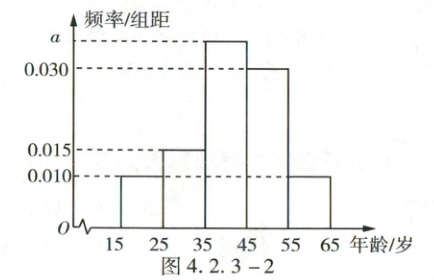
（1）求这200人年龄的平均数（同一组数据用该区间的中点值作代表）和中位数（精确到小数点后一位）；
（2）现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人，再从这5人中随机抽取3人进行问卷调查，求第2组恰好抽取2人的概率；
（3）若从所有参与调查的人（人数很多）中任意选出3人，设其中关注环境治理和保护问题的人数X为随机变量，求X的分布列。

答案：
解析 （1）由$10×(0.010+0.015+a+0.030+0.010)=1$，得$a=0.035$，
平均数为$20×0.1+30×0.15+40×0.35+50×0.3+60×0.1=41.5$。
设中位数为x，则$10×0.010+10×0.015+(x-35)×0.035=0.5$，$\therefore x\approx42.1$。
（2）由题意知，从第1,2组抽取的人数分别为2,3。
设第2组中恰好抽取2人的事件为A，则$P(A)=\frac{ C_{2}^{1} C_{3}^{2}}{ C_{5}^{3}}=\frac{3}{5}$。
（3）从所有参与调查的人中任意选出1人，此人关注环境治理和保护问题的概率为$\frac{4}{5}$，
易知X的所有可能取值为0,1,2,3，
$\therefore P(X=0)= C_{3}^{0}(1-\frac{4}{5})^{3}=\frac{1}{125}$，
$P(X=1)= C_{3}^{1}(\frac{4}{5})^{1}(1-\frac{4}{5})^{2}=\frac{12}{125}$，
$P(X=2)= C_{3}^{2}(\frac{4}{5})^{2}(1-\frac{4}{5})^{1}=\frac{48}{125}$，
$P(X=3)= C_{3}^{3}(\frac{4}{5})^{3}=\frac{64}{125}$，
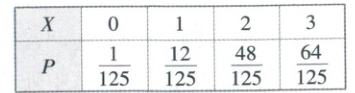
$\therefore$X的分布列为