《2026年高考领航卷物理》

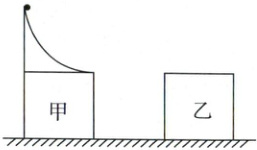
14. (12分)如图所示,光滑水平面上有两个相同的正方体物块甲、乙,甲固定在地面上,乙不固定,甲上固定四分之一圆轨道,圆轨道半径、正方体棱长均为$L$,圆轨道下端水平。开始时,甲、乙的距离为$L$。一小球从轨道顶端静止下滑。小球与物块乙碰撞时,小球竖直速度不变,水平方向遵循弹性碰撞规律。已知物块乙的质量为$M$,小球的质量为$m$,小球可视为质点。
(1)求小球与物块乙的碰撞点的离地高度;
(2)若$M = 9m$,求小球与物块乙碰后瞬间各自的水平速度大小;
(3)请计算说明能否通过改变物块乙的质量,使小球在落地前与物块甲相碰。

答案： 14.机械能守恒、动量守恒+分析综合能力
解：
(1)设小球离开圆轨道时速度大小为$v_0$
由机械能守恒定律有$mgL=\frac{1}{2}mv_0^2$(1分)
时间$t_1=\frac{L}{v_0}$(1分)
下落距离$\Delta h=\frac{1}{2}gt_1^2$(1分)
小球与物块乙的碰撞点的离地高度$h=L-\Delta h=\frac{3}{4}L$(1分)
(2)小球与物块乙碰撞过程水平方向动量守恒、机械能守恒
$mv_0=Mv_2 - mv_1$(1分)
$\frac{1}{2}mv_0^2=\frac{1}{2}mv_1^2+\frac{1}{2}Mv_2^2$(1分)
联立解得碰后瞬间小球水平速度大小为$v_1=\frac{M - m}{m + M}v_0=\frac{4}{5}\sqrt{2gL}$(1分)
物块乙水平速度大小为$v_2=\frac{2m}{m + M}v_0=\frac{1}{5}\sqrt{2gL}$(1分)
(3)若无物块乙，则$L=\frac{1}{2}gt^2$
小球落地时水平位移$x=v_0t=2L$(1分)
可知若小球与物块乙碰后瞬间水平速度大小仍为$v_0$，则小球落地时恰好与物块甲的底部相碰(1分)
由
(2)中分析可知，与物块乙碰后瞬间小球的水平速度大小为$v_球=\frac{M - m}{m + M}v_0＜v_0$(1分)
故不能通过改变物块乙的质量，使小球在落地前与物块甲相碰(1分)