2026年高考领航卷物理
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年高考领航卷物理 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
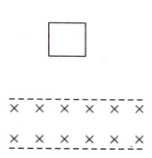
10. 如图所示,相距为$d$的两水平虚线间存在垂直纸面向里、磁感应强度大小为$B$的匀强磁场,正方形金属线框质量为$m$、电阻为$R$、边长为$L(L < d)$,从距离磁场上边界一定高度处由静止释放,线框刚好匀速进入磁场。线框完全出磁场瞬间的速度为$v$,已知重力加速度为$g$,忽略空气阻力。下列说法正确的是
A.线框开始进磁场时的速度大小为$\frac{mgR}{B^2d^2}$
B.线框从进入磁场到出磁场过程所用时间为$\frac{mR(B^2L^2v - mgR) + 2B^4L^5}{mgRB^2L^2}$
C.全过程中,线框产生的焦耳热不大于$mg(d + L)$
D.线框进磁场过程中,通过线框某横截面的电荷量为$\frac{BL^2}{R}$

A.线框开始进磁场时的速度大小为$\frac{mgR}{B^2d^2}$
B.线框从进入磁场到出磁场过程所用时间为$\frac{mR(B^2L^2v - mgR) + 2B^4L^5}{mgRB^2L^2}$
C.全过程中,线框产生的焦耳热不大于$mg(d + L)$
D.线框进磁场过程中,通过线框某横截面的电荷量为$\frac{BL^2}{R}$
答案:
10.BCD 电磁感应+分析综合能力
过程拆解
线框刚好匀速进入磁场线框受力平衡线框开始进磁场时的速度
线框开始进入磁场到出磁场过程的时间
第一步:根据受力平衡求解线框进磁场时的速度 设线框进磁场时的速度为$v_0$,由于线框匀速进入磁场,受力平衡,则$F_{A1}=mg$,又$F_{A1}=BIL$,$I=\frac{E}{R}$,$E=BLv_0$,解得$v_0=\frac{mgR}{B^2L^2}$,A错误。
第二步:结合平均电流和动量定理求解时间 平均安培力$\overline{F_A}=B\overline{I}L=\frac{B^2L^3\overline{v}}{R}$,则线框进磁场过程安培力冲量大小为$I_1=\overline{F_{A1}}\Delta t_1=\frac{B^2L^3}{R}$,线框出磁场过程安培力冲量大小为$I_2=\overline{F_{A2}}\Delta t_2=\frac{B^2L^3}{R}$,所以全过程中线框所受安培力的冲量大小为$I=I_1+I_2=\frac{2B^2L^3}{R}$[点拨:也可以通过$I=F_At=BLIt=BLq$的思路来求解安培力冲量大小]。线框从进入磁场到出磁场过程中,由动量定理可得$I_c-I_A=mgt-\frac{2B^2L^3}{R}=mv-mv_0$,则总时间$t=\frac{mR(B^2L^2v-mgR)+2B^4L^5}{mgRB^2L^2}$,B正确。
第三步:根据能量守恒定律分析线框中产生焦耳热与对应量的关系 由能量守恒定律可得$\frac{1}{2}mv_0^2+mg(d+L)=\frac{1}{2}mv^2+Q$,分析可知$v\geq v_0$[点拨:$d>L$,线框匀速进入磁场,然后做自由落体运动,最后在重力和安培力作用下出磁场;线框出磁场过程中,一定先做减速运动,若速度可以减小为$v_0$,则此时线框受力平衡,开始做匀速运动,出磁场过程中速度不会再减小,即一定有$v\geq v_0$],则$Q\leq mg(d+L)$,C正确。
第四步:求解电荷量 由$q=\overline{I}\Delta t_1$,$\overline{I}=\frac{\overline{E}}{R}$,$\overline{E}=BL\overline{v}$可得$q=\frac{BL^2}{R}$[点拨:$q=\frac{\Delta\Phi}{R}$],D正确。
过程拆解
线框刚好匀速进入磁场线框受力平衡线框开始进磁场时的速度
线框开始进入磁场到出磁场过程的时间
第一步:根据受力平衡求解线框进磁场时的速度 设线框进磁场时的速度为$v_0$,由于线框匀速进入磁场,受力平衡,则$F_{A1}=mg$,又$F_{A1}=BIL$,$I=\frac{E}{R}$,$E=BLv_0$,解得$v_0=\frac{mgR}{B^2L^2}$,A错误。
第二步:结合平均电流和动量定理求解时间 平均安培力$\overline{F_A}=B\overline{I}L=\frac{B^2L^3\overline{v}}{R}$,则线框进磁场过程安培力冲量大小为$I_1=\overline{F_{A1}}\Delta t_1=\frac{B^2L^3}{R}$,线框出磁场过程安培力冲量大小为$I_2=\overline{F_{A2}}\Delta t_2=\frac{B^2L^3}{R}$,所以全过程中线框所受安培力的冲量大小为$I=I_1+I_2=\frac{2B^2L^3}{R}$[点拨:也可以通过$I=F_At=BLIt=BLq$的思路来求解安培力冲量大小]。线框从进入磁场到出磁场过程中,由动量定理可得$I_c-I_A=mgt-\frac{2B^2L^3}{R}=mv-mv_0$,则总时间$t=\frac{mR(B^2L^2v-mgR)+2B^4L^5}{mgRB^2L^2}$,B正确。
第三步:根据能量守恒定律分析线框中产生焦耳热与对应量的关系 由能量守恒定律可得$\frac{1}{2}mv_0^2+mg(d+L)=\frac{1}{2}mv^2+Q$,分析可知$v\geq v_0$[点拨:$d>L$,线框匀速进入磁场,然后做自由落体运动,最后在重力和安培力作用下出磁场;线框出磁场过程中,一定先做减速运动,若速度可以减小为$v_0$,则此时线框受力平衡,开始做匀速运动,出磁场过程中速度不会再减小,即一定有$v\geq v_0$],则$Q\leq mg(d+L)$,C正确。
第四步:求解电荷量 由$q=\overline{I}\Delta t_1$,$\overline{I}=\frac{\overline{E}}{R}$,$\overline{E}=BL\overline{v}$可得$q=\frac{BL^2}{R}$[点拨:$q=\frac{\Delta\Phi}{R}$],D正确。
11. (6分)某实验小组要测量弹簧的劲度系数,他们利用手机自带的定位传感器、小布袋和质量均相等的若干玻璃球,设计了图甲所示的实验装置。实验步骤如下:
①按图甲安装实验器材,弹簧上端固定在横杆上,下端与手机连接,手机重心和弹簧在同一竖直线上;
②手托着手机缓慢下移直到手离开手机,手机静止时,打开定位传感器,将此位置定为初始位置;
③在小布袋中放入5颗玻璃球,将小布袋挂在手机下方,手托着手机缓慢下移直到手离开手机,待手机静止时记录手机相对于初始位置的位移$x$;
④增加玻璃球的颗数,重复上述操作,记录放入玻璃球的个数$n$与相应的位移$x$,根据记录数据作出$n - x$图像,如图乙所示。
回答下列问题:
(1)已知每颗玻璃球的质量为2 g,当地重力加速度$g = 9.8 m/s^2$,由图乙可以求得弹簧的劲度系数为N/m,小布袋质量为g。
(2)$n - x$图像末端出现弯曲的原因是:________________________。

①按图甲安装实验器材,弹簧上端固定在横杆上,下端与手机连接,手机重心和弹簧在同一竖直线上;
②手托着手机缓慢下移直到手离开手机,手机静止时,打开定位传感器,将此位置定为初始位置;
③在小布袋中放入5颗玻璃球,将小布袋挂在手机下方,手托着手机缓慢下移直到手离开手机,待手机静止时记录手机相对于初始位置的位移$x$;
④增加玻璃球的颗数,重复上述操作,记录放入玻璃球的个数$n$与相应的位移$x$,根据记录数据作出$n - x$图像,如图乙所示。
回答下列问题:
(1)已知每颗玻璃球的质量为2 g,当地重力加速度$g = 9.8 m/s^2$,由图乙可以求得弹簧的劲度系数为N/m,小布袋质量为g。
(2)$n - x$图像末端出现弯曲的原因是:________________________。

答案:
11.【答案】
(1)$19.6$(2分)$20$(2分)
(2)弹簧形变量超出了弹性限度(2分)
【评分标准】
(2)表述合理即可得分。
【解题思路】
(1)设手机的质量为M,挂上手机平衡后弹簧形变量为$x_0$,根据胡克定律和平衡条件有$kx_0=Mg$。设小布袋和一颗玻璃球的质量分别为$m_0$、m,挂上装入玻璃球的小布袋平衡后,根据胡克定律和平衡条件有$k(x_0+x)=Mg+m_0g+nmg$。联立得$n=\frac{k}{mg}x-\frac{m_0}{m}$,结合图乙可知,图像斜率为$\frac{k}{mg}=\frac{20 - 10}{(3 - 2)×10^{-2}m}=\frac{10}{0.01m}=19.6N/m$。由图乙可知,当$x = 1cm = 0.01m$时$n = 0$,又$k = 19.6N/m$,代入$n=\frac{k}{mg}x-\frac{m_0}{m}$,解得$m_0 = 20g$。
(2)当弹簧形变量超出弹性限度时,随着玻璃球数量的增加,弹簧形变量增加量逐渐变小或不再增加,n - x图像末端会向右下弯曲。
(1)$19.6$(2分)$20$(2分)
(2)弹簧形变量超出了弹性限度(2分)
【评分标准】
(2)表述合理即可得分。
【解题思路】
(1)设手机的质量为M,挂上手机平衡后弹簧形变量为$x_0$,根据胡克定律和平衡条件有$kx_0=Mg$。设小布袋和一颗玻璃球的质量分别为$m_0$、m,挂上装入玻璃球的小布袋平衡后,根据胡克定律和平衡条件有$k(x_0+x)=Mg+m_0g+nmg$。联立得$n=\frac{k}{mg}x-\frac{m_0}{m}$,结合图乙可知,图像斜率为$\frac{k}{mg}=\frac{20 - 10}{(3 - 2)×10^{-2}m}=\frac{10}{0.01m}=19.6N/m$。由图乙可知,当$x = 1cm = 0.01m$时$n = 0$,又$k = 19.6N/m$,代入$n=\frac{k}{mg}x-\frac{m_0}{m}$,解得$m_0 = 20g$。
(2)当弹簧形变量超出弹性限度时,随着玻璃球数量的增加,弹簧形变量增加量逐渐变小或不再增加,n - x图像末端会向右下弯曲。
查看更多完整答案,请扫码查看


