《2026年高考领航卷物理》

7. 如图所示,理想变压器原线圈与电阻$R_1$串联后接在$u = 250\sqrt{2}\sin(100\pi t) V$的交流电源两端。已知电阻箱接入电路的阻值为$40\Omega$时,电流表示数为1 A,电阻箱接入电路的阻值为$15\Omega$时,电流表示数为2 A,电流表为理想交流电表,则


A.交流电的频率为100 Hz
B.电阻$R_1$的阻值为100 $\Omega$
C.变压器原、副线圈匝数比为$4:1$
D.电流表示数为1 A时,电路总功率为50 W

答案： 7.D 理想变压器变压、变流规律 由交流电表达式$u=U_m\sin\omega t=250\sqrt{2}\sin(100\pi t)V$可知，圆频率$\omega=100\pi rad/s$，交流电频率$f=\frac{\omega}{2\pi}=50Hz$，A错误。设变压器原副线圈匝数的比值为k，电流表示数为I，则原线圈两端电压$U_1=kU_2=kIR_2$，又$U_1=\frac{U_m}{\sqrt{2}}-\frac{R_1}{k}I$，将$I = 1A$、$R_2 = 40\Omega$及$I = 2A$、$R_2 = 15\Omega$代入，解得$k = 5$，$R_1 = 250\Omega$，BC错误。电阻箱接入电路的阻值$R_2 = 40\Omega$时，电流表示数$I = 1A$，电路总功率$P=P_1+P_2=(\frac{I}{k})^2R_1+I^2R_2=50W$，D正确。

8. 一列简谐横波沿$x$轴传播,波源位于坐标原点$O$处,从$t = 0$时刻开始振动,$t = 5 s$时波刚好传到$x = 10 m$处,波形如图所示,下列说法正确的是

A.该波的波速为2 m/s

B.波源起振的方向沿$y$轴正方向
C.当$t = 10 s$时$x = 10 m$处的质点在波峰
D.$x = 2 m$处质点的振动方程为$y = 2\sin(\frac{\pi}{2}t + \frac{\pi}{2})cm(t \geq 1 s)$

答案：
8.AD 机械波的传播

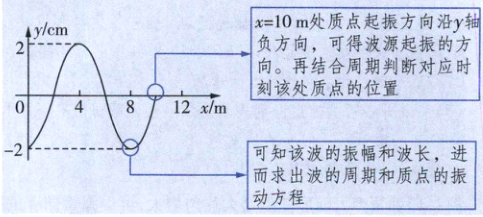
据图析题：$x = 10m$处质点起振方向沿y轴负方向，可得波源起振的方向沿y轴负方向。再结合周期判断对应时刻该处质点的位置。
波速$v=\frac{\Delta x}{\Delta t}=\frac{10m}{5s}=2m/s$，A正确。根据同侧法可知，$t = 5s$时$x = 10m$处质点沿y轴负方向运动，则波源起振的方向沿y轴负方向[点拨：各质点起振的方向与波源起振的方向相同]，B错误。由图可知波长$\lambda = 8m$，则周期$T=\frac{\lambda}{v}=\frac{8m}{2m/s}=4s$。$t = 10s$时$x = 10m$处质点振动时间为$\Delta t'=5s=1\frac{1}{4}T$，质点起振方向沿y轴负方向，则$t = 10s$时$x = 10m$处质点在波谷，C错误。振幅$A = 2cm$，圆频率$\omega=\frac{2\pi}{T}=\frac{\pi}{2}rad/s$，$x = 2m$处质点的振动方程为$y = 2\sin(\frac{\pi}{2}t+\varphi)cm$。当$t=\frac{\Delta x'}{v}=\frac{2m}{2m/s}=1s$时波传到该点，则有$0 = 2\sin(\frac{\pi}{2}×1+\varphi)cm$，解得$\varphi=\frac{\pi}{2}$或$\varphi=-\frac{\pi}{2}$，由于质点起振方向沿y轴负方向，则$\varphi=\frac{\pi}{2}$，故$x = 2m$处的质点的振动方程为$y = 2\sin(\frac{\pi}{2}t+\frac{\pi}{2})cm(t\geq1s)$，D正确。

9. 如图所示,一光滑半圆形支架固定在竖直平面内,半径为$R$,圆心为$O$,$AB$为竖直直径,圆弧上穿一小球,可沿圆弧滑动。两根相同橡皮筋一端固定在小球上,另一端分别固定在$A$、$B$点。初始时小球在$P$点,由静止释放小球,$\angle PAB = 60^{\circ}$,$\angle QAB = 30^{\circ}$,橡皮筋伸长量在弹性限度内。已知橡皮筋原长为$R$,满足胡克定律,劲度系数为$k$,小球可视为质点,重力加速度为$g$,下列说法正确的是


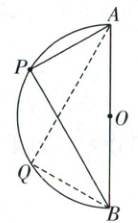
A.小球运动到$Q$点时速度大小为$\sqrt{gR}$
B.小球运动到$Q$点时速度大小为$\sqrt{2gR}$
C.若小球运动到$Q$点时速度恰好达最大值,则小球质量为$\frac{(3 - \sqrt{3})kR}{3g}$
D.若小球运动到$Q$点时速度恰好达最大值,则小球质量为$\frac{(3\sqrt{3} - 1)kR}{3g}$

答案： 9.BC 机械能守恒+逻辑推理能力 由题可知，小球在P、Q点时都是一根橡皮筋处于原长，另一根橡皮筋伸长，且伸长的橡皮筋的伸长量相同，则小球在P、Q点时橡皮筋具有的总弹性势能相同。设小球质量为m，从P到Q根据机械能守恒定律有$mg(2R\sin60°×\sin60°-2R\cos60°×\cos60°)=\frac{1}{2}mv^2$，解得$v=\sqrt{2gR}$，A错误，B正确。若小球运动到Q点时速度恰好达最大值，则小球切向加速度为0，切向所受合力为零，有$mg\cos30°=k(2R\sin60°-R)\cos60°$，解得$m=\frac{(3-\sqrt{3})kR}{3g}$，C正确，D错误。