《2026年高考领航卷数学》

18. (17分)
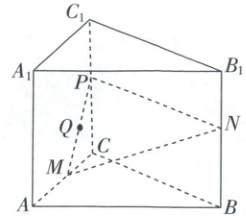
如图，在直三棱柱$ A B C - A _ { 1 } B _ { 1 } C _ { 1 } $中，$ A B = 4 $，$ B C = 2 \sqrt { 3 } $，$ \angle A B C = \frac { \pi } { 6 } $，$ A A _ { 1 } = 3 $。若$ M $，$ N $分别为棱$ A C $，$ B B _ { 1 } $上的动点，且$ M N = 2 \sqrt { 5 } $，点$ N $在平面$ A _ { 1 } A C C _ { 1 } $上的射影为点$ P $，线段$ M P $的中点为$ Q $。
(1)求证：平面$ B C C _ { 1 } B _ { 1 } \perp $平面$ A _ { 1 } A C C _ { 1 } $；
(2)求点$ Q $的轨迹长度；
(3)求直线$ A B $与平面$ M N P $所成角的正弦值的取值范围。

答案：
18.面面垂直+线面角的正弦值+动点的轨迹
解:
(1)第一步:利用勾股定理的逆定理证明$ BC \perp AC $
在$ \triangle ABC $中,由余弦定理得$ AC^2 = AB^2 + BC^2 - 2AB · BC · \cos \angle ABC = 4^2 + (2\sqrt{3})^2 - 2 × 4 × 2\sqrt{3} × \cos \frac{\pi}{6} = 4 $,
所以$ AC = 2 $,
则$ AB^2 = AC^2 + BC^2 $,所以$ BC \perp AC $。 (2分)
第二步:结合直棱柱的几何特征及线面垂直的判定定理证明$ BC \perp $平面$ A_1ACC_1 $
由题可得$ BC \perp CC_1 $,(直棱柱的几何特征的应用)
因为$ AC \cap CC_1 = C $,$ AC,CC_1 \subset $平面$ A_1ACC_1 $,所以$ BC \perp $平面$ A_1ACC_1 $。 (3分)
第三步:利用面面垂直的判定定理证得结论
又$ BC \subset $平面$ BCC_1B_1 $,所以平面$ BCC_1B_1 \perp $平面$ A_1ACC_1 $。 (4分)
评分标准 ①求出$ AC = 2 $给1分,证得$ BC \perp AC $再给1分;②证明线面垂直时缺少相交条件不给分。
(2)解法一 第一步:建立空间直角坐标系,设出$ M,N $的坐标,结合线段长求出坐标间的关系
以$ C $为坐标原点,$ \overrightarrow{CA} $的方向为$ x $轴正方向,$ \overrightarrow{CB} $的方向为$ y $轴正方向,$ \overrightarrow{CC_1} $的方向为$ z $轴正方向,建立如图所示的空间直角坐标系,

设$ M(a, 0, 0) $,$ N(0, 2\sqrt{3}, b) (0 \leq a \leq 2, 0 \leq b \leq 3) $,
因为$ MN = 2\sqrt{5} $,
所以$ \sqrt{(a - 0)^2 + (0 - 2\sqrt{3})^2 + (0 - b)^2} = 2\sqrt{5} $,整理得$ a^2 + b^2 = 8 $。 (6分)
第二步:利用中点坐标公式表示出点$ Q $的坐标,并结合换元法得到点$ Q $坐标间的关系
因为$ NP \perp $平面$ A_1ACC_1 $,且平面$ BCC_1B_1 \perp $平面$ A_1ACC_1 $,
所以点$ P $在线段$ CC_1 $上,则$ P(0, 0, b) $,所以$ Q\left( \frac{a}{2}, 0, \frac{b}{2} \right) $,(中点坐标公式的应用)
又点$ Q $在平面$ xCz $内,不妨设$ Q(x, 0, z) $,则$ x = \frac{a}{2} $,$ z = \frac{b}{2} $,于是$ a = 2x $,$ b = 2z $,
所以$ (2x)^2 + (2z)^2 = 8 $,即$ x^2 + z^2 = 2 $。 (8分)
第三步:找到点$ Q $的轨迹,即可得解
当点$ M $与$ A $重合时,$ a = 2 $,则$ b = 2 $,即$ x = 1 $时,$ z = 1 $;
当点$ M $与$ C $重合时,$ a = 0 $,则$ b = 2\sqrt{2} $,即$ x = 0 $时,$ z = \sqrt{2} $。
故点$ Q $的轨迹是以$ C $为圆心,$ \sqrt{2} $为半径的圆的一段圆弧,且其所对的圆心角等于$ \frac{\pi}{4} $, (10分)
因此点$ Q $的轨迹长度为$ \sqrt{2} × \frac{\pi}{4} = \frac{\sqrt{2}}{4}\pi $。 (11分)
评分标准 ①建系给1分,得到$ a^2 + b^2 = 8 $再给1分;②求出点$ Q\left( \frac{a}{2}, 0, \frac{b}{2} \right) $给1分,得到$ x^2 + z^2 = 2 $再给1分;③得到点$ Q $在以$ C $为圆心,$ \sqrt{2} $为半径的圆上也给1分。
解法二 因为点$ N $在平面$ A_1ACC_1 $上的射影为点$ P $,
所以$ NP \perp $平面$ A_1ACC_1 $, (5分)
则$ NP // BC $,且点$ P $在线段$ CC_1 $上,故$ NP = BC = 2\sqrt{3} $, (6分)
易知$ NP \perp PM $,所以$ PM = \sqrt{MN^2 - NP^2} = \sqrt{20 - 12} = 2\sqrt{2} $, (7分)
连接$ CQ $,当$ M $与$ C $重合时,易知$ CQ = \frac{1}{2}PM = \sqrt{2} $,当$ M $与$ C $不重合时,在$ \mathrm{Rt} \triangle PMC $中,$ CQ = \frac{1}{2}PM = \sqrt{2} $,(在直角三角形中,斜边上的中线等于斜边的一半)
所以点$ Q $在以$ C $为圆心,$ \sqrt{2} $为半径的圆上。 (8分)
当点$ M $与$ A $重合时,$ BN = PC = 2 $,$ \triangle MCP $为等腰直角三角形,
此时点$ Q $所在的位置$ Q_1 $满足$ \angle ACQ_1 = \angle PCQ_1 = \frac{\pi}{4} $;
当点$ M $与$ C $重合时,$ BN = PC = 2\sqrt{2} $,此时点$ Q $所在的位置$ Q_2 $在$ PC $上。
所以点$ Q $的轨迹是以$ C $为圆心,$ \sqrt{2} $为半径的圆中,从$ Q_1 $到$ Q_2 $的一段圆弧,且$ \angle Q_1CQ_2 = \frac{\pi}{4} $,如图所示,
(10分)
因此点$ Q $的轨迹长度为$ \sqrt{2} × \frac{\pi}{4} = \frac{\sqrt{2}}{4}\pi $。 (11分)
评分标准 得到点$ M $的两种极限情况,一种给1分。
(3)第一步:写出相关点、向量的坐标及$ b $的范围
由
(2)的解法一可得$ A(2, 0, 0) $,$ B(0, 2\sqrt{3}, 0) $,$ M(a, 0, 0) $,$ N(0, 2\sqrt{3}, b) $,$ P(0, 0, b) $,
所以$ \overrightarrow{AB} = (-2, 2\sqrt{3}, 0) $,$ \overrightarrow{MN} = (-a, 2\sqrt{3}, b) $,$ \overrightarrow{MP} = (-a, 0, b) $。 (12分)
由
(2)的解法一知$ a^2 + b^2 = 8 $,又$ 0 \leq a \leq 2 $,所以$ 2 \leq b \leq 2\sqrt{2} $。 (13分)
第二步:求平面$ MNP $的法向量
设平面$ MNP $的法向量为$ \boldsymbol{n} = (x', y', z') $,
则$ \begin{cases} \overrightarrow{MN} · \boldsymbol{n} = 0 \\ \overrightarrow{MP} · \boldsymbol{n} = 0 \end{cases} $,即$ \begin{cases} -ax' + 2\sqrt{3}y' + bz' = 0 \\ -ax' + bz' = 0 \end{cases} $,
取$ x' = 1 $,则$ y' = 0 $,$ z' = \frac{a}{b} $,于是$ \boldsymbol{n} = \left( 1, 0, \frac{a}{b} \right) $。 (14分)
第三步:借助向量的夹角公式求线面角的正弦值
设直线$ AB $与平面$ MNP $所成角为$ \theta $,
则$ \sin \theta = |\cos \langle \overrightarrow{AB}, \boldsymbol{n} \rangle| = \frac{|\overrightarrow{AB} · \boldsymbol{n}|}{|\overrightarrow{AB}||\boldsymbol{n}|} = \frac{|-2|}{4 × \sqrt{1 + \left( \frac{a}{b} \right)^2}} = \frac{1}{2\sqrt{\frac{b^2 + a^2}{b^2}}} = \frac{b}{4\sqrt{2}} $。 (16分)
第四步:结合$ b $的范围,即可得解
又$ 2 \leq b \leq 2\sqrt{2} $,所以$ \frac{\sqrt{2}}{4} \leq \frac{b}{4\sqrt{2}} \leq \frac{1}{2} $,即$ \frac{\sqrt{2}}{4} \leq \sin \theta \leq \frac{1}{2} $,
故直线$ AB $与平面$ MNP $所成角的正弦值的取值范围是$ \left[ \frac{\sqrt{2}}{4}, \frac{1}{2} \right] $。 (17分)
评分标准 ①正确得到相关向量的坐标即可给1分;②正确求出平面$ MNP $的其他法向量同样给1分。
方法技巧 解决空间中动点的轨迹问题时,要从动中求静,从运动变化中发现不变的位置关系或数量关系,进而转化为常规几何问题求解。在解题时,可以建立空间直角坐标系,通过坐标寻求动点满足的条件,分析动点的轨迹;也可以根据题意,将空间中动点的轨迹从几何体中抽离出来,并作出平面图形,进而利用平面几何的相关知识进行求解。