2026年高考领航卷数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年高考领航卷数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
17. (15分)
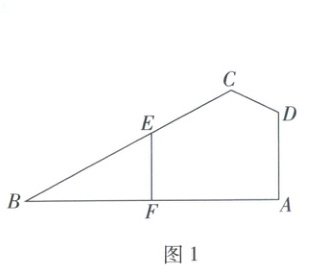
如图1,在四边形$ ABCD $中,$ AB \perp AD $,$ \angle ABC = 30^{\circ} $,$ \angle ADC = \angle BCD $,点$ E $满足$ \overrightarrow{BE} = \frac{3}{5}\overrightarrow{BC} $,$ F $为$ AB $的中点,$ AB = 6\sqrt{3} $,$ BE = 6 $。将$ \triangle BEF $沿$ EF $翻折至$ \triangle GEF $,使得$ GC = 8 $,如图2。
(1) 证明:$ GF \perp $平面$ AFECD $。
(2) 已知$ M $,$ N $分别在线段$ GE $,$ GF $上,且$ NC = 7 $,$ GM = \frac{1}{2}ME $。
(i) 证明:$ AD // $平面$ MNC $;
(ii) 求二面角$ A - DN - C $的正弦值。

如图1,在四边形$ ABCD $中,$ AB \perp AD $,$ \angle ABC = 30^{\circ} $,$ \angle ADC = \angle BCD $,点$ E $满足$ \overrightarrow{BE} = \frac{3}{5}\overrightarrow{BC} $,$ F $为$ AB $的中点,$ AB = 6\sqrt{3} $,$ BE = 6 $。将$ \triangle BEF $沿$ EF $翻折至$ \triangle GEF $,使得$ GC = 8 $,如图2。
(1) 证明:$ GF \perp $平面$ AFECD $。
(2) 已知$ M $,$ N $分别在线段$ GE $,$ GF $上,且$ NC = 7 $,$ GM = \frac{1}{2}ME $。
(i) 证明:$ AD // $平面$ MNC $;
(ii) 求二面角$ A - DN - C $的正弦值。


答案:
17.线面垂直+线面平行+二面角的正弦值
解:
(1)在题图1中连接AE,在$\triangle ABE$中,$AB = 6\sqrt{3},$BE = 6,$\angle ABE = 30^{\circ},$所以$AE^2 = AB^2 + BE^2 - 2AB · BE \cos \angle ABE = (6\sqrt{3})^2 + 6^2 - 2×6\sqrt{3} × 6 × \cos 30^{\circ} = 36,$(余弦定理的应用)故AE = 6,又F为AB的中点,所以$EF \perp AB,$EF = 3,所以$GF \perp EF。$由$\overrightarrow{BE} = \frac{3}{5}\overrightarrow{BC},$得EC = 4,易知$\angle BEF = \angle AE$
解:
(1)在题图1中连接AE,在$\triangle ABE$中,$AB = 6\sqrt{3},$BE = 6,$\angle ABE = 30^{\circ},$所以$AE^2 = AB^2 + BE^2 - 2AB · BE \cos \angle ABE = (6\sqrt{3})^2 + 6^2 - 2×6\sqrt{3} × 6 × \cos 30^{\circ} = 36,$(余弦定理的应用)故AE = 6,又F为AB的中点,所以$EF \perp AB,$EF = 3,所以$GF \perp EF。$由$\overrightarrow{BE} = \frac{3}{5}\overrightarrow{BC},$得EC = 4,易知$\angle BEF = \angle AE$
查看更多完整答案,请扫码查看


