《2026年高考领航卷数学》

19.（17分）
如图，在三棱柱$ABC - A_{1}B_{1}C_{1}$中，$AB = AC$，点$A_{1}$在平面$ABC$上的射影为$BC$的中点$O$。
（1）求证：四边形$BCC_{1}B_{1}$是矩形；
（2）若$AB \perp AC$，$BC = BB_{1} = 2$，求二面角$B - AB_{1} - C$的正弦值；
（3）记三棱柱$ABC - A_{1}B_{1}C_{1}$的体积为$V$，线段$CC_{n}(n \in \mathbf{N}^{*})$的中点为$C_{n + 1}$，三棱锥$C_{n} - AB_{1}C$的体积为$V_{n}$，若$T_{n} = \frac{(n + 2)V_{n}}{n(n + 1)}$，求证：$T_{1} + T_{2} + ·s + T_{n} ＜ \frac{2V}{3}$。

答案：
19.垂直关系的证明+二面角正弦值的计算+三棱锥的体积+等比数列+裂项相消法求和
解:
(1)第一步:连接$AO$,利用线面垂直的判定定理证明$BC\perp$平面$AOA_{1}$
如图,连接$AO$,因为$O$为$BC$的中点,$AB = AC$,所以$AO\perp BC$。
因为点$A_{1}$在平面$ABC$上的射影为$BC$的中点$O$,所以$A_{1}O\perp$平面$ABC$,
因为$BC\subset$平面$ABC$,所以$A_{1}O\perp BC$,
因为$AO\cap A_{1}O=O$,所以$BC\perp$平面$AOA_{1}$。
第二步:利用线面垂直的性质证明$AA_{1}\perp BC$
因为$AA_{1}\subset$平面$AOA_{1}$,所以$AA_{1}\perp BC$。
第三步:利用三棱柱的性质证明四边形$BCC_{1}B_{1}$是矩形
因为$AA_{1}// BB_{1}$,所以$BB_{1}\perp BC$,
又四边形$BCC_{1}B_{1}$是平行四边形,所以四边形$BCC_{1}B_{1}$是矩形。

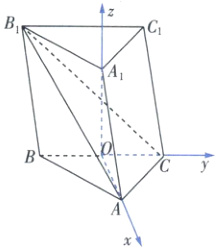
(2)第一步:建立空间直角坐标系,求相关点及向量的坐标
由
(1)知$OA$,$OC$,$OA_{1}$两两垂直,以$O$为坐标原点,直线$OA$,$OC$,$OA_{1}$分别为$x$,$y$,$z$轴建立如图所示的空间直角坐标系,
则$A(1,0,0)$,$B(0,-1,0)$,$C(0,1,0)$,$A_{1}(0,0,\sqrt{3})$,所以$\overrightarrow{AB}=(-1,-1,0)$,$\overrightarrow{AC}=(-1,1,0)$,$\overrightarrow{AA_{1}}=(-1,0,\sqrt{3})$,
$\overrightarrow{AB_{1}}=\overrightarrow{AB}+\overrightarrow{AA_{1}}=(-1,-1,0)+(-1,0,\sqrt{3})=(-2,-1,\sqrt{3})$。
第二步:分别求平面$ABB_{1}$与平面$ACB_{1}$的法向量
设平面$ABB_{1}$的法向量为$\boldsymbol{n}_{1}=(x_{1},y_{1},z_{1})$,
则$\begin{cases}\boldsymbol{n}_{1}·\overrightarrow{AB}=0\\\boldsymbol{n}_{1}·\overrightarrow{AB_{1}}=0\end{cases}$即$\begin{cases}-x_{1}-y_{1}=0\\-2x_{1}-y_{1}+\sqrt{3}z_{1}=0\end{cases}$,
取$z_{1}=1$,得$\boldsymbol{n}_{1}=(\sqrt{3},-\sqrt{3},1)$。
设平面$ACB_{1}$的法向量为$\boldsymbol{n}_{2}=(x_{2},y_{2},z_{2})$,
则$\begin{cases}\boldsymbol{n}_{2}·\overrightarrow{AC}=0\\\boldsymbol{n}_{2}·\overrightarrow{AB_{1}}=0\end{cases}$,即$\begin{cases}-x_{2}+y_{2}=0\\-2x_{2}-y_{2}+\sqrt{3}z_{2}=0\end{cases}$,
取$x_{2}=1$,得$\boldsymbol{n}_{2}=(1,1,\sqrt{3})$。
第三步:求二面角$B-AB_{1}-C$的正弦值
设二面角$B-AB_{1}-C$的平面角的大小为$\theta$,
则$\vert\cos\theta\vert=\frac{\vert\boldsymbol{n}_{1}·\boldsymbol{n}_{2}\vert}{\vert\boldsymbol{n}_{1}\vert\vert\boldsymbol{n}_{2}\vert}=\frac{\vert\sqrt{3}×1+(-\sqrt{3})×1+1×\sqrt{3}\vert}{\sqrt{(\sqrt{3})^{2}+(-\sqrt{3})^{2}+1^{2}}×\sqrt{1^{2}+1^{2}+(\sqrt{3})^{2}}}=\frac{\sqrt{3}}{\sqrt{7}×\sqrt{5}}=\frac{\sqrt{3}}{\sqrt{35}}$,
所以$\sin\theta=\sqrt{1-\cos^{2}\theta}=\sqrt{1-\frac{3}{35}}=\sqrt{\frac{32}{35}}=\frac{4\sqrt{70}}{35}$,
即二面角$B-AB_{1}-C$的正弦值为$\frac{4\sqrt{70}}{35}$。
(3)第一步:确定数列$\{V_{n}\}$是等比数列,并求其通项公式
由题可得$V_{1}=V_{C_{1}-ABC}=V_{A_{1}-ABC}=V_{B-ABC}=\frac{1}{3}V$,
因为$C_{n+1}$为线段$CC_{n}$的中点,所以$V_{n+1}=\frac{1}{2}V_{n}$,
所以数列$\{V_{n}\}$是首项为$\frac{1}{3}V$,公比为$\frac{1}{2}$的等比数列,
所以$V_{n}=\frac{1}{3}V×(\frac{1}{2})^{n-1}=\frac{V}{3×2^{n-1}}$。
第二步:利用裂项相消法求和,并结合放缩法即可得证
所以$T_{n}=\frac{(n+2)V_{n}}{n(n+1)}=\frac{(n+2)V}{3n(n+1)2^{n-1}}=\frac{2V}{3}[\frac{1}{n×2^{n-1}}-\frac{1}{(n+1)×2^{n}}]$,
所以$T_{1}+T_{2}+·s+T_{n}=\frac{2V}{3}[\frac{1}{1×1}-\frac{1}{2×2}+\frac{1}{2×2}-\frac{1}{3×2^{2}}+·s+\frac{1}{n×2^{n-1}}-\frac{1}{(n+1)×2^{n}}]=\frac{2V}{3}[1-\frac{1}{(n+1)×2^{n}}]＜\frac{2V}{3}$。