《2026年高考领航卷数学》

7. 某人工智能团队在训练深度学习模型时,采用分阶段学习率衰减策略。第一阶段使用对数衰减,初始学习率为0.1，学习率$ \eta $随迭代次数$ n ( n \in \mathbf { N } ^ { * } ) $的变化公式为$ \eta = 0.1 - 0.01 \ln ( n + 1 ) $。当学习率小于等于0.05时,切换至第二阶段,第二阶段使用指数衰减策略,学习率公式为$ \eta = 0.05 \mathrm { e } ^ { - 0.01 ( n - n _ { 1 } ) } $，其中$ n _ { 1 } $为第一阶段结束时的迭代次数，$ n $为总迭代次数。当学习率小于等于0.01时,模型停止训练。则该模型需要训练的总迭代次数为(结果保留整数。参考数据:$ \mathrm { e } ^ { 5 } \approx 148.413 $，$ \ln 5 \approx 1.609 $)

A.307
B.308
C.309
D.310

答案： 7.C 函数模型+指数型、对数型函数的单调性+指数、对数运算 令$ \eta = 0.1 - 0.01\ln(n + 1) = 0.05 $,则$ \ln(n + 1) = 5 $,所以$ n + 1 = e^5 $,于是$ n = e^5 - 1 \approx 148.413 - 1 = 147.413 $,由于$ n\in \mathbf{N}^* $,且$ \eta = 0.1 - 0.01\ln(n + 1) $随$ n $的增大而减小,所以第一阶段结束时的迭代次数$ n_1 = 148 $。
令$ \eta = 0.05e^{-0.01(n - n_1)} = 0.01 $,则$ e^{-0.01(n - 148)} = 0.2 $,得$ n = 148 + 100\ln 5 $,又$ 100\ln 5 \approx 100 × 1.609 = 160.9 $,$ n\in \mathbf{N}^* $,且$ \eta = 0.05e^{-0.01(n - n_1)} $随$ n $的增大而减小,所以该模型需要训练的总迭代次数$ n = 148 + 161 = 309 $,故选C。

8. 已知$ O $为坐标原点，椭圆$ C : \frac { x ^ { 2 } } { a ^ { 2 } } + \frac { y ^ { 2 } } { b ^ { 2 } } = 1 ( a ＞ b ＞ 0 ) $的左焦点为$ F _ { 1 } $，过点$ F _ { 1 } $的直线$ \sqrt { 3 } x + 3 y + 1 = 0 $与$ C $的一个交点$ P $位于第四象限，若$ \triangle O P F _ { 1 } $为等腰三角形，则$ C $的离心率为

A.$ \frac { 2 } { 3 } $
B.$ \frac { \sqrt { 3 } } { 2 } $
C.$ \sqrt { 3 } - 1 $
D.$ \frac { \sqrt { 3 } - 1 } { 2 } $

答案： 8.C 椭圆的定义、几何性质+直线与椭圆的位置关系
思维导引 先由直线$ \sqrt{3}x + 3y + 1 = 0 $过点$ F_1 $,求出$ F_1 $的坐标,再由直线方程求出直线$ PF_1 $的倾斜角,得$ \angle OF_1P = 30° $,由$ \triangle OPF_1 $为等腰三角形、点$ P $在第四象限,知$ |OP| = |OF_1| = \frac{\sqrt{3}}{3} $,$ \angle F_1OP = 120° $,从而可以写出点$ P $的坐标,根据点$ P $在椭圆上,即可得到关于$ a,b $的方程,再根据$ a^2 = b^2 + c^2 $与离心率公式即可得解。
解法一 $ \sqrt{3}x + 3y + 1 = 0 $中,令$ y = 0 $,得$ x = -\frac{\sqrt{3}}{3} $,因为直线$ \sqrt{3}x + 3y + 1 = 0 $过点$ F_1 $,所以$ c = |OF_1| = \frac{\sqrt{3}}{3} $,由直线$ PF_1 $的斜率为$ -\frac{\sqrt{3}}{3} $,得直线$ PF_1 $的倾斜角为$ 150° $,所以$ \angle OF_1P = 30° $。由$ \triangle OPF_1 $为等腰三角形,而点$ P $在第四象限,知$ |OP| = |OF_1| = \frac{\sqrt{3}}{3} $,得$ \angle F_1OP = 120° $,(若等腰三角形$ OPF_1 $的底边为$ OF_1 $或$ OP $,则点$ P $不可能位于第四象限)
于是点$ P $的坐标为$ \left( \frac{\sqrt{3}}{6}, -\frac{1}{2} \right) $,由点$ P $在$ C $上,得$ \frac{1}{12a^2} + \frac{1}{4b^2} = 1 $,又$ a^2 = b^2 + \frac{1}{3} $,所以$ 36a^4 - 24a^2 + 1 = 0 $,得$ a^2 = \frac{2 + \sqrt{3}}{6} $,故$ \frac{c^2}{a^2} = \frac{\frac{1}{3}}{\frac{2 + \sqrt{3}}{6}} = 4 - 2\sqrt{3} $,所以$ C $的离心率为$ \frac{c}{a} = \sqrt{3} - 1 $,故选C。
解法二 $ \sqrt{3}x + 3y + 1 = 0 $中,令$ y = 0 $,得$ x = -\frac{\sqrt{3}}{3} $,
因为直线$ \sqrt{3}x + 3y + 1 = 0 $过点$ F_1 $,所以$ c = |OF_1| = \frac{\sqrt{3}}{3} $,由直线$ PF_1 $的斜率为$ -\frac{\sqrt{3}}{3} $,得直线$ PF_1 $的倾斜角为$ 150° $,所以$ \angle OF_1P = 30° $。由$ \triangle OPF_1 $为等腰三角形,而点$ P $在第四象限,知$ |OP| = |OF_1| = \frac{\sqrt{3}}{3} $,得$ \angle F_1OP = 120° $,所以$ |F_1P| = \sqrt{3}|OP| = 1 $。设$ F_2 $为$ C $的右焦点,连接$ PF_2 $,由椭圆的定义得$ |PF_2| = 2a - 1 $。在$ \triangle PF_1F_2 $中,由余弦定理得$ (2a - 1)^2 = 1 + \frac{4}{3} - 2 × 1 × \frac{2\sqrt{3}}{3} × \frac{\sqrt{3}}{2} = \frac{1}{3} $,得$ 2a = 1 + \frac{\sqrt{3}}{3} $,又$ 2c = \frac{2\sqrt{3}}{3} $,所以$ C $的离心率$ e = \frac{2c}{2a} = \frac{\frac{2\sqrt{3}}{3}}{1 + \frac{\sqrt{3}}{3}} = \sqrt{3} - 1 $,故选C。
解法三 由$ \triangle OPF_1 $为等腰三角形,而点$ P $在第四象限,知$ |OP| = |OF_1| $。(若等腰三角形$ OPF_1 $的底边为$ OF_1 $或$ OP $,则点$ P $不可能位于第四象限)
设$ F_2 $为椭圆的右焦点,连接$ PF_2 $,又$ |OF_2| = |OF_1| $,所以$ |OP| = |OF_1| = |OF_2| $,所以$ PF_1 \perp PF_2 $。由直线$ PF_1 $的斜率为$ -\frac{\sqrt{3}}{3} $,得直线$ PF_1 $的倾斜角为$ 150° $,所以$ \angle OF_1P = 30° $,则$ |PF_1| = \sqrt{3}c $,$ |PF_2| = c $,则$ |PF_1| + |PF_2| = 2a = \sqrt{3}c + c = (\sqrt{3} + 1)c $,(椭圆定义的应用)
故$ C $的离心率$ e = \frac{c}{a} = \frac{2}{\sqrt{3} + 1} = \sqrt{3} - 1 $,故选C。
方法技巧 求椭圆离心率(或范围)的方法
(1)根据已知条件列方程组,解出$ a,c $的值,直接利用离心率公式求解即可；
(2)根据已知条件得到一个关于$ a,c $(或$ a,b $)的齐次方程(或不等式),然后转化为关于离心率$ e $的方程(或不等式)求解；
(3)因为离心率是比值,所以有时也可以利用特殊值法,例如令$ a = 1 $,求出相应的$ c $的值,进而求出离心率。

9. 已知等比数列$ \left\{ a _ { n } \right\} $的公比为$ q $，前$ n $项和为$ S _ { n } $，$ a _ { 3 } = 4 $，则下列结论中一定正确的是

A.若$ a _ { 6 } = - 32 $，则$ q = \pm 2 $
B.$ a _ { 2 } a _ { 6 } a _ { 7 } = a _ { 5 } ^ { 3 } $
C.若$ a _ { 6 } = \frac { 1 } { 2 } $，则$ a _ { 1 } a _ { 2 } a _ { 3 } · ·s · a _ { n } $的最大值为1024
D.$ S _ { 2 } $，$ S _ { 4 } - S _ { 2 } $，$ S _ { 6 } - S _ { 4 } $构成等比数列

答案： 9.BC 等比数列的通项公式+等比数列的性质+等比数列求和
A(×)由已知得$ \begin{cases} a_1q^2 = 4 \\ a_1q^5 = -32 \end{cases} $,所以$ q^3 = -8 $,解得$ q = -2 $。
B(√)由于$ \{a_n\} $为等比数列,所以$ a_2a_6a_7 = (a_3a_5)a_7 = a_5(a_3a_7) = a_5 · a_5^2 = a_5^3 $。
C(√)通解 由已知得$ \begin{cases} a_1q^2 = 4 \\ a_1q^5 = \frac{1}{2} \end{cases} $,所以$ \begin{cases} a_1 = 16 \\ q = \frac{1}{2} \end{cases} $,因此$ a_1a_2a_3 · ·s · a_n = a_1^n q^{1 + 2 + ·s + (n - 1)} = 16^n \left( \frac{1}{2} \right)^{\frac{n(n - 1)}{2}} = 2^{-\frac{1}{2}n^2 + \frac{9}{2}n} = 2^{-\frac{1}{2}\left( n - \frac{9}{2} \right)^2 + \frac{81}{8}} $,所以当$ n = 4 $或$ 5 $时,$ a_1a_2a_3 · ·s · a_n $取最大值,且最大值为$ 2^{10} = 1024 $。(技巧:借助二次函数的图象与性质求最值)
优解 由$ a_3 = 4 $,$ a_6 = \frac{1}{2} $,得$ q^3 = \frac{a_6}{a_3} = \frac{1}{8} $,得$ q = \frac{1}{2} $,所以$ a_5 = a_3q^2 = 1 $,故当$ n ＞ 5 $时,$ a_n ＜ 1 $,当$ n \leq 5 $时,$ a_n \geq 1 $,所以当$ n = 4 $或$ n = 5 $时,$ a_1a_2a_3 · ·s · a_n $取得最大值,且最大值为$ a_1a_2a_3a_4 = 16 × 8 × 4 × 2 = 1024 $。
D(×)解法一 数列$ S_2,S_4 - S_2,S_6 - S_4 $,即数列$ a_1 + a_2,a_3 + a_4,a_5 + a_6 $,即数列$ a_1 + a_2,(a_1 + a_2)q^2,(a_1 + a_2)q^4 $,当$ a_1 + a_2 \neq 0 $,即$ q \neq -1 $时,$ S_2,S_4 - S_2,S_6 - S_4 $构成等比数列,当$ a_1 + a_2 = 0 $,即$ q = -1 $时,$ S_2,S_4 - S_2,S_6 - S_4 $不构成等比数列。
解法二 当$ q = -1 $时,$ S_2 = S_4 - S_2 = S_6 - S_4 = 0 $,此时$ S_2,S_4 - S_2,S_6 - S_4 $不构成等比数列。
故选BC。
结论拓展 若等比数列$ \{a_n\} $的前$ n $项和为$ S_n $,公比为$ q(q \neq -1) $,则$ S_n,S_{2n} - S_n,S_{3n} - S_{2n},·s $也构成等比数列,且公比为$ q^n $。

10. 已知实数$ x $，$ \theta $满足$ x + \frac { 1 } { x } = 2 \cos \theta $，则下列结论中正确的是

A.$ x \cos \theta = \pm 1 $
B.$ x - \frac { 1 } { x } = 2 \sin \theta $
C.$ x ^ { 2 } + \frac { 1 } { x ^ { 2 } } = 2 \cos 2 \theta $
D.$ x ^ { 3 } + \frac { 1 } { x ^ { 3 } } = 2 \cos 3 \theta $

答案： 10.BCD 基本不等式+三角恒等变换 解法一 由基本不等式可得$ \left| x + \frac{1}{x} \right| = |x| + \left| \frac{1}{x} \right| \geq 2\sqrt{|x| · \left| \frac{1}{x} \right|} = 2 $,当且仅当$ |x| = 1 $时取等号。又$ |2\cos \theta| \leq 2 $,所以$ \left| x + \frac{1}{x} \right| = |2\cos \theta| = 2 $。当$ x = 1 $时,可得$ \cos \theta = 1 $,$ \sin \theta = 0 $;当$ x = -1 $时,可得$ \cos \theta = -1 $,$ \sin \theta = 0 $。
A(×)当$ x = 1 $时,$ x\cos \theta = 1 $,当$ x = -1 $时,$ x\cos \theta = 1 $。所以$ x\cos \theta = 1 $。
B(√)当$ x = 1 $时,$ x - \frac{1}{x} = 0 = 2\sin \theta $,当$ x = -1 $时,$ x - \frac{1}{x} = 0 = 2\sin \theta $。所以$ x - \frac{1}{x} = 2\sin \theta $。
C(√)$ 2\cos 2\theta = 2(2\cos^2 \theta - 1) = 4\cos^2 \theta - 2 $,(二倍角公式的应用)
当$ x = 1 $时,$ x^2 + \frac{1}{x^2} = 2 = 2\cos 2\theta $,当$ x = -1 $时,$ x^2 + \frac{1}{x^2} = 2 = 2\cos 2\theta $。所以$ x^2 + \frac{1}{x^2} = 2\cos 2\theta $。
D(√)$ \cos 3\theta = \cos(2\theta + \theta) = \cos 2\theta \cos \theta - \sin 2\theta \sin \theta = (2\cos^2 \theta - 1)\cos \theta - 2\sin^2 \theta \cos \theta = 2\cos^3 \theta - \cos \theta - 2(1 - \cos^2 \theta)\cos \theta = 4\cos^3 \theta - 3\cos \theta $,(两角和的余弦公式、二倍角公式、同角三角函数的基本关系的应用)
所以$ 2\cos 3\theta = 8\cos^3 \theta - 6\cos \theta $。当$ x = 1 $时,$ x^3 + \frac{1}{x^3} = 2 = 2\cos 3\theta $,当$ x = -1 $时,$ x^3 + \frac{1}{x^3} = -2 = 2\cos 3\theta $。所以$ x^3 + \frac{1}{x^3} = 2\cos 3\theta $。
故选BCD。
解法二 由$ x + \frac{1}{x} = 2\cos \theta $可得$ x^2 - 2\cos \theta · x + 1 = 0 $,易知$ \Delta = 4\cos^2 \theta - 4 \geq 0 $。因为$ |\cos \theta| \leq 1 $,所以$ 4\cos^2 \theta - 4 \leq 0 $,从而$ 4\cos^2 \theta - 4 = 0 $,于是$ \cos \theta = \pm 1 $。当$ \cos \theta = 1 $时,可得$ x = 1 $,$ \sin \theta = 0 $;当$ \cos \theta = -1 $时,可得$ x = -1 $,$ \sin \theta = 0 $。
A(×)当$ \cos \theta = 1 $时,$ x\cos \theta = 1 $,当$ \cos \theta = -1 $时,$ x\cos \theta = 1 $。所以$ x\cos \theta = 1 $。
B(√)当$ \cos \theta = 1 $时,$ x - \frac{1}{x} = 0 = 2\sin \theta $,当$ \cos \theta = -1 $时,$ x - \frac{1}{x} = 0 = 2\sin \theta $。所以$ x - \frac{1}{x} = 2\sin \theta $。
C(√)$ 2\cos 2\theta = 2(2\cos^2 \theta - 1) = 4\cos^2 \theta - 2 $,(二倍角公式的应用)
当$ \cos \theta = 1 $时,$ x^2 + \frac{1}{x^2} = 2 = 2\cos 2\theta $,当$ \cos \theta = -1 $时,$ x^2 + \frac{1}{x^2} = 2 = 2\cos 2\theta $。所以$ x^2 + \frac{1}{x^2} = 2\cos 2\theta $。
D(√)$ \cos 3\theta = \cos(2\theta + \theta) = \cos 2\theta \cos \theta - \sin 2\theta \sin \theta = (2\cos^2 \theta - 1)\cos \theta - 2\sin^2 \theta \cos \theta = 2\cos^3 \theta - \cos \theta - 2(1 - \cos^2 \theta)\cos \theta = 4\cos^3 \theta - 3\cos \theta $,(两角和的余弦公式、二倍角公式、同角三角函数的基本关系的应用)
所以$ 2\cos 3\theta = 8\cos^3 \theta - 6\cos \theta $。当$ x = 1 $时,$ x^3 + \frac{1}{x^3} = 2 = 2\cos 3\theta $,当$ x = -1 $时,$ x^3 + \frac{1}{x^3} = -2 = 2\cos 3\theta $。所以$ x^3 + \frac{1}{x^3} = 2\cos 3\theta $。
故选BCD。
结论拓展 ①若实数$ x,\theta $满足$ x + \frac{1}{x} = 2\cos \theta $,则$ x^n + \frac{1}{x^n} = 2\cos n\theta (n\in \mathbf{N}^*) $;②三角函数中的三倍角公式$ \sin 3\theta = 3\sin \theta - 4\sin^3 \theta $,$ \cos 3\theta = 4\cos^3 \theta - 3\cos \theta $。

11. 如图1，在直角梯形$ A _ { 1 } A _ { 2 } A _ { 3 } D $中，$ A _ { 1 } D // A _ { 2 } A _ { 3 } $，$ A _ { 1 } A _ { 2 } \perp A _ { 1 } D $，$ A _ { 1 } D = 5 $，$ A _ { 1 } A _ { 2 } = 4 $，$ B $，$ C $分别为$ A _ { 1 } A _ { 2 } $，$ A _ { 2 } A _ { 3 } $的中点，现把$ \triangle A _ { 1 } B D $，$ \triangle A _ { 2 } B C $，$ \triangle A _ { 3 } C D $分别沿$ B D $，$ B C $，$ C D $折起，使得点$ A _ { 1 } $，$ A _ { 2 } $，$ A _ { 3 } $重合为一点$ A $，得到如图2所示的四面体$ A B C D $，则下列说法正确的是

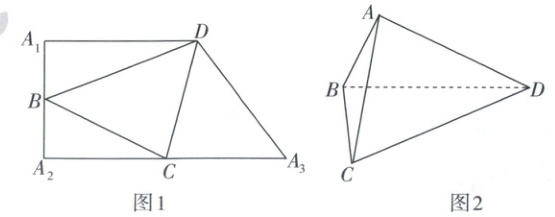
A.$ A B \perp C D $
B.四面体$ A B C D $的体积为$ \frac { 32 } { 3 } $
C.点$ A $到底面$ B C D $的距离为$ \frac { 16 } { 9 } $
D.二面角$ A - B C - D $的余弦值为$ \frac { 4 \sqrt { 5 } } { 9 } $

答案：
11.AC 线面位置关系+四面体的体积+点到平面的距离+二面角的余弦值
A(√)在直角梯形$ A_1A_2A_3D $中,$ A_1B \perp A_1D $,$ A_2B \perp A_2C $,则在四面体$ ABCD $中,$ AB \perp AD $,$ AB \perp AC $,因为$ AC \cap AD = A $,$ AC,AD \subset $平面$ ACD $,所以$ AB \perp $平面$ ACD $,(线面垂直的判定定理的应用)
又$ CD \subset $平面$ ACD $,所以$ AB \perp CD $。
B(×)在直角梯形$ A_1A_2A_3D $中,过$ D $作$ DE \perp A_2A_3 $于点$ E $。因为$ A_1A_2 = 4 $,所以$ ED = 4 $,因为$ A_1D = A_3D = 5 $,所以$ EA_3 = 3 $,所以$ A_2A_3 = 5 + 3 = 8 $,所以$ A_2C = A_3C = 4 $,因为$ B $为$ A_1A_2 $的中点,所以$ A_1B = A_2B = 2 $。所以在四面体$ ABCD $中,$ AB = 2 $,$ AC = 4 $,$ AD = 5 $,所以$ S_{\triangle ACD} = S_{\triangle A_3CD} = \frac{1}{2} × 4 × 4 = 8 $,又$ AB \perp $平面$ ACD $,所以$ V_{ABCD} = V_{B - ACD} = \frac{1}{3} × 8 × 2 = \frac{16}{3} $。
C(√)由选项B可得直角梯形$ A_1A_2A_3D $的面积$ S = \frac{1}{2} × (A_1D + A_2A_3) × A_1A_2 = 26 $,$ S_{\triangle ABD} = \frac{1}{2}A_1B × A_1D = 5 $,$ S_{\triangle ABC} = \frac{1}{2}A_2B × A_2C = 4 $,$ S_{\triangle A_3CD} = 8 $,故$ S_{\triangle BCD} = S - S_{\triangle ABD} - S_{\triangle ABC} - S_{\triangle A_3CD} = 26 - 5 - 4 - 8 = 9 $。设点$ A $到底面$ BCD $的距离为$ h $,由选项B知$ V_{A - BCD} = \frac{1}{3}S_{\triangle BCD} · h = \frac{16}{3} $,得$ h = \frac{16}{9} $。
D(×)如图,在四面体$ ABCD $中,过$ A $作$ AO \perp $平面$ BCD $,经判断知点$ O $在$ \triangle BCD $内,

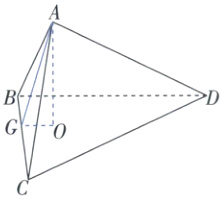
过$ A $作$ AG \perp BC $于点$ G $,连接$ OG $,则$ OG \perp BC $,所以$ \angle AGO $为二面角$ A - BC - D $的平面角。在$ \mathrm{Rt} \triangle ABC $中,$ \frac{1}{2}AB · AC = \frac{1}{2}BC · AG $,得$ AG = \frac{AB · AC}{BC} = \frac{2 × 4}{2\sqrt{5}} = \frac{4\sqrt{5}}{5} $,由选项C知$ OA = h = \frac{16}{9} $,所以$ \sin \angle AGO = \frac{AO}{AG} = \frac{\frac{16}{9}}{\frac{4\sqrt{5}}{5}} = \frac{4\sqrt{5}}{9} $,所以$ \cos \angle AGO = \frac{1}{9} $,即二面角$ A - BC - D $的余弦值为$ \frac{1}{9} $。
故选AC。