《2026年高考领航卷数学》

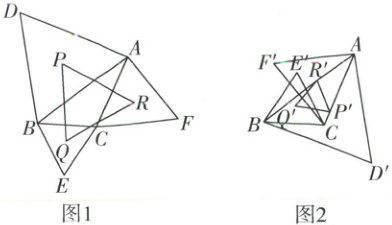
14. 一般地,若从任意三角形的三边分别向外作等边三角形,则这三个等边三角形的中心连接起来构成一个等边三角形,这个等边三角形称为原三角形的外拿破仑三角形;若从任意三角形的三边分别向内作等边三角形,则这三个等边三角形的中心连接起来也构成一个等边三角形,这个等边三角形称为原三角形的内拿破仑三角形。在 $ \triangle ABC $ 中,已知 $ A = \frac{\pi}{6},BC = 6,\triangle ABC $ 的外拿破仑三角形 $ PQR $（如图 1）的面积为 $ S_1 $,内拿破仑三角形 $ P'Q'R' $（如图 2）的面积为 $ S_2 $,则 $ S_1 - S_2 $ 的最大值等于____。

答案： 14. 9(2 + $\sqrt{3}$) 外拿破仑三角形、内拿破仑三角形+正、余弦定理+三角形面积
第一步：结合外拿破仑三角形的定义求△PQR的面积
在题图1中连接AP,AR,在△ABC中,设AB = c,AC = b,BC = a,则由外拿破仑三角形的定义得AP = $\frac{\sqrt{3}}{3}$c,AR = $\frac{\sqrt{3}}{3}$b,∠PAR = ∠PAB + ∠BAC + ∠CAR = $\frac{\pi}{6}$ + $\frac{\pi}{6}$ + $\frac{\pi}{6}$ = $\frac{\pi}{2}$,(点拨:设等边三角形的边长为a,外接圆半径为R,则2R = $\frac{a}{\sin\frac{\pi}{3}}$ = $\frac{2\sqrt{3}}{3}$a,所以R = $\frac{\sqrt{3}}{3}$a。由等边三角形“三线合一”的性质知,AP、AR分别是∠DAB、∠FAC的平分线,所以∠PAB = $\frac{1}{2}$∠DAB = $\frac{\pi}{6}$,∠CAR = $\frac{1}{2}$∠FAC = $\frac{\pi}{6}$)
所以由勾股定理得PR² = $\frac{1}{3}$(b² + c²),所以S₁ = $\frac{\sqrt{3}}{4}$PR² = $\frac{\sqrt{3}}{12}$(b² + c²)。
第二步：结合内拿破仑三角形的定义求得△P'Q'R'的面积,进而求得S₁ - S₂
在题图2中连接AP',AR',由内拿破仑三角形的定义得AP' = $\frac{\sqrt{3}}{3}$c,AR' = $\frac{\sqrt{3}}{3}$b,∠P'AR' = ∠P'AB + ∠R'AC - ∠BAC = $\frac{\pi}{6}$,所以由余弦定理得P'R'² = $\frac{1}{3}$(b² + c² - $\sqrt{3}$bc),所以S₂ = $\frac{\sqrt{3}}{4}$P'R'² = $\frac{\sqrt{3}}{12}$(b² + c² - $\sqrt{3}$bc),所以S₁ - S₂ = $\frac{1}{4}$bc。
第三步：利用余弦定理、基本不等式求S₁ - S₂的最大值
在△ABC中,因为∠BAC = $\frac{\pi}{6}$,BC = 6,所以由余弦定理得b² + c² - $\sqrt{3}$bc = 36,因为b² + c²≥2bc,所以(2 - $\sqrt{3}$)bc≤36,所以bc≤36(2 + $\sqrt{3}$),所以S₁ - S₂ = $\frac{1}{4}$bc≤9(2 + $\sqrt{3}$),当且仅当b = c = 3$\sqrt{6}$ + 3$\sqrt{2}$时,S₁ - S₂取得最大值,为9(2 + $\sqrt{3}$)。
结论拓展 一般地,若一个三角形的内、外拿破仑三角形都存在,则外拿破仑三角形的面积与内拿破仑三角形的面积的差等于原三角形的面积。

15. (13分)
已知等差数列 $ \{2a_n - b_n\} $ 的公差为 2,等比数列 $ \{2a_n + b_n\} $ 的公比为 2,且 $ a_1 = b_1 = 1 $。
(1) 求数列 $ \{a_n\} $ 的通项公式;
(2) 求数列 $ \{\frac{4a_n^2 - b_n^2}{3}\} $ 的前 $ n $ 项和 $ T_n $。

答案： 15.等差数列+等比数列+数列求和
解:
(1)第一步:写出等差数列{2aₙ - bₙ}的通项公式
因为等差数列{2aₙ - bₙ}的公差为2,2a₁ - b₁ = 1,
所以2aₙ - bₙ = 1 + 2(n - 1) = 2n - 1。① (2分)
第二步:写出等比数列{2aₙ + bₙ}的通项公式
因为等比数列{2aₙ + bₙ}的公比为2,2a₁ + b₁ = 3,
所以2aₙ + bₙ = 3×2ⁿ⁻¹。② (4分)
第三步:两式相加求得{aₙ}的通项公式
由① + ②得4aₙ = 2n - 1 + 3×2ⁿ⁻¹,
则aₙ = $\frac{1}{4}$(2n - 1) + 3×2ⁿ⁻³。 (6分)
评分标准 {aₙ}的通项公式写成其他等价形式同样给分。
(2)解法一 第一步:结合
(1)求得$\frac{4aₙ² - bₙ²}{3}$的通项公式
由
(1)知$\frac{4aₙ² - bₙ²}{3}$ = $\frac{(2aₙ - bₙ)(2aₙ + bₙ)}{3}$ = (2n - 1)2ⁿ⁻¹,
(另解:也可以分别求出{aₙ},{bₙ}的通项公式,再代入$\frac{4aₙ² - bₙ²}{3}$求解) (8分)
第二步:利用错位相减法求和
所以Tₙ = 1×1 + 3×2 + 5×2² + … + (2n - 1)2ⁿ⁻¹,
2Tₙ = 1×2 + 3×2² + 5×2³ + … + (2n - 1)2ⁿ。 (10分)
两式相减得 -Tₙ = 1 + 2(2 + 2² + … + 2ⁿ⁻¹) - (2n - 1)2ⁿ
= 1 + 2×$\frac{2(1 - 2ⁿ⁻¹)}{1 - 2}$ - (2n - 1)2ⁿ
= - 3 - (2n - 3)2ⁿ,
所以Tₙ = 3 + (2n - 3)2ⁿ。 (13分)
评分标准 ①Tₙ列式正确即可给1分;②正确写出 -Tₙ的表达式给1分,化简正确再给1分。
解法二 第一步:结合
(1)求得$\frac{4aₙ² - bₙ²}{3}$的通项公式
由
(1)知$\frac{4aₙ² - bₙ²}{3}$ = $\frac{(2aₙ - bₙ)(2aₙ + bₙ)}{3}$ = (2n - 1)2ⁿ⁻¹,
(另解:也可以分别求出{aₙ},{bₙ}的通项公式,再代入$\frac{4aₙ² - bₙ²}{3}$求解) (8分)
第二步:利用裂项相消法求Tₙ
易知(2n - 1)2ⁿ⁻¹ = (2n - 3)2ⁿ - (2n - 5)2ⁿ⁻¹。 (10分)
所以Tₙ = [(-1)×2 - (-3)×1] + [1×2² - (-1)×2] + [3×2³ - 1×2²] + … + [(2n - 3)2ⁿ - (2n - 5)2ⁿ⁻¹] = -(-3)×1 + (2n - 3)2ⁿ = 3 + (2n - 3)2ⁿ。 (13分)
评分标准 Tₙ列式正确给1分,结果正确给2分。
方法技巧 数列求和的常用方法
1.公式法:直接利用等差、等比数列的前n项和公式求和。
2.分组求和法:将数列的通项转化为若干个可求和的新数列的通项之和,从而求得原数列的前n项和。
3.错位相减法:适用于通项为一个等差数列和一个等比数列通项相乘的形式。
4.裂项相消法:将通项拆成两项之差的形式,然后让各项相加,中间项相互抵消,剩余的有限项相加,得到数列的前n项和。

16. (15分)
已知函数 $ f(x) = xe^{k x}(k \in \mathbf{R}) $。
(1) 若 $ f(x) $ 在 $ [-1,1] $ 上不单调,求 $ k $ 的取值范围;
(2) 当 $ k = 1 $ 时,若对任意的 $ x ＞ 0,f(x) ＞ x^2 + a x $ 恒成立,求实数 $ a $ 的取值范围。

答案： 16.函数的单调性+零点存在定理+导数的应用+由不等式恒成立求参数的取值范围
解:
(1)第一步:结合导数,将原问题转化为方程有解问题
因为f(x) = xeᵏˣ(k∈R),所以f'(x) = eᵏˣ(kx + 1)。
因为f(x)在[-1,1]上不单调,
所以f'(x) = eᵏˣ(kx + 1) = 0在(-1,1)上有解。(3分)
第二步:构造函数,利用零点存在定理求解k的取值范围
设h(x) = kx + 1,
因为eᵏˣ ＞ 0,所以当x∈(-1,1)时,h(x) = 0有解,
(5分)
所以h
(1)h(-1) = (1 + k)(1 - k) ＜ 0,(零点存在定理的应用)
解得k ＜ -1或k ＞ 1。
故实数k的取值范围为(-∞,-1)∪(1,+∞)。 (8分)
评分标准 体现零点存在定理给2分,得到k的取值范围给1分。
(2)第一步:利用分离参数法将问题进行转化
当k = 1时,f(x) = xeˣ,
因为x ＞ 0,所以由f(x) ＞ x² + ax得a ＜ eˣ - x,(分离参数法的应用)
第二步:构造函数,利用导数知识求y = eˣ - x的取值范围
设p(x) = eˣ - x(x≥0),则p'(x) = eˣ - 1≥0。 (12分)
所以p(x)在[0,+∞)上单调递增,
所以当x ＞ 0时,p(x) ＞ p
(0) = 1。 (14分)
第三步:得到实数a的取值范围
所以实数a的取值范围为(-∞,1]。(提示:注意对1的取舍，本题中eˣ - x取不到1,故a可以取到1) (15分)
方法技巧 分离参数法解决不等式恒成立问题的步骤
(1)将参数分离出来,转化为f(x) ＞ a或f(x) ＜ a的形式。
(2)通过研究函数f(x)的性质求得f(x)的最值。
(3)得参数a的取值范围。