《2026年高考领航卷数学》

17. (15分)
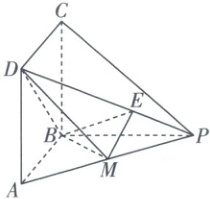
【漳州市2026届高三第一次质检】如图，点$ P $为正方形$ ABCD $所在平面外一点，$ M $为$ PA $中点，$ \overrightarrow{DE} = \lambda \overrightarrow{DP}(0 ＜ \lambda ＜ 1) $。
(1) 求证：$ PC // $平面$ BDM $。
(2) 若平面$ ABCD \perp $平面$ ABP $，$ AB = BP = 2 $，$ AB \perp BP $。
(i) 当$ \lambda = \frac{2}{3} $时，求证：$ PD \perp $平面$ BEM $；

(ii) 当二面角$ D - BM - E $的正弦值为$ \frac{\sqrt{6}}{9} $时，求$ \lambda $的值。

答案：
17. 线面平行的判定+线面垂直的判定+二面角
解法一：
(1) 连接AC交BD于点Q，连接QM，因为四边形ABCD是正方形，所以Q为AC的中点，又M为PA的中点，所以在△PAC中，有QM // PC，因为QM ⊂平面BDM，PC ⊄平面BDM，所以PC //平面BDM。
(2) 在正方形ABCD中，有BC ⊥ AB，因为平面ABCD ⊥平面ABP，平面ABCD ∩平面ABP = AB，BC ⊂平面ABCD，所以BC ⊥平面ABP，因为BP ⊂平面ABP，所以BC ⊥ BP，又AB ⊥ BP，故以B为原点，分别以BA，BP，BC的方向为x轴、y轴、z轴的正方向建立空间直角坐标系，如图所示，

则B(0, 0, 0)，P(0, 2, 0)，D(2, 0, 2)，A(2, 0, 0)，M(1, 1, 0)，DP = (-2, 2, -2)，DE = (-2λ, 2λ, -2λ)，BD = (2, 0, 2)，BM = (1, 1, 0)。
(i) 当λ = 2/3时，DE = (-4/3, 4/3, -4/3)，BE = BD + DE = (2/3, 4/3, 2/3)，所以DP · BE = -2 × (2/3) + 2 × (4/3) - 2 × (2/3) = 0，DP · BM = -2 × 1 + 2 × 1 - 2 × 0 = 0，所以DP ⊥ BE，DP ⊥ BM，即PD ⊥ BE，PD ⊥ BM，又BE ⊂平面BEM，BM ⊂平面BEM，BM ∩ BE = B，所以PD ⊥平面BEM。
(ii) 设n = (x₁, y₁, z₁)为平面BDM的法向量，则{n · BD = 0；n · BM = 0}，即{2x₁ + 2z₁ = 0；x₁ + y₁ = 0}，取x₁ = 1，得y₁ = -1，z₁ = -1，则n = (1, -1, -1)是平面BDM的一个法向量。
BE = BD + DE = (2 - 2λ, 2λ, 2 - 2λ)，设m = (x₂, y₂, z₂)为平面BEM的法向量，则{m · BE = 0；m · BM = 0}，即{(2 - 2λ)x₂ + 2λy₂ + (2 - 2λ)z₂ = 0；x₂ + y₂ = 0}，得(1 - 2λ)x₂ + (1 - λ)z₂ = 0，取x₂ = λ - 1，得y₂ = 1 - λ，z₂ = 1 - 2λ，则m = (λ - 1, 1 - λ, 1 - 2λ)是平面BEM的一个法向量。
因为二面角D - BM - E的正弦值为√6/9，所以sin ＜m, n＞ = √6/9，所以cos² ＜m, n＞ = 1 - (√6/9)² = 25/27，即(4λ - 3)²/(3 × (6λ² - 8λ + 3)) = 25/27，化简得3λ² + 8λ - 3 = 0，解得λ = 1/3或λ = -3（舍去），所以λ的值为1/3。
解法二：
(1) 同解法一。
(2)(i) 第一步：利用面面垂直的性质定理得到AD ⊥平面ABP。因为四边形ABCD为正方形，所以AD ⊥ AB，因为平面ABCD ⊥平面ABP，平面ABCD ∩平面ABP = AB，AD ⊂平面ABCD，所以AD ⊥平面ABP。
第二步：利用线面垂直的判定定理得到BM ⊥平面ADP，进而得到BM ⊥ PD。因为BM ⊂平面ABP，所以AD ⊥ BM。又AB = BP，M为AP的中点，所以BM ⊥ AP，又AD ∩ AP = A，所以BM ⊥平面ADP，又PD ⊂平面ADP，所以BM ⊥ PD。
第三步：解三角形得到PD ⊥ EM。因为AB = BP = 2，AB ⊥ BP，所以AP = 2√2，所以PM = √2，PD = √(AD² + AP²) = 2√3，PE = 2√3/3，在Rt△ADP中，cos ∠DPA = AP/PD = 2√2/2√3 = √6/3，在△EMP中，由余弦定理可得EM² = PE² + PM² - 2PE × PM cos ∠EPM = 4/3 + 2 - 2 × (2√3/3) × √2 × √6/3 = 2/3，所以PM² = PE² + EM²，所以PE ⊥ EM，即PD ⊥ EM。
第四步：根据线面垂直的判定定理证得PD ⊥平面BEM。又EM ∩ BM = M，所以PD ⊥平面BEM。
(ii) 第一步：找出二面角D - BM - E的平面角。因为BM ⊥平面ADP，DM，EM ⊂平面ADP，所以BM ⊥ DM，BM ⊥ EM，又DM ⊂平面DBM，EM ⊂平面BME，所以二面角D - BM - E的平面角为∠DME。
第二步：得到∠DME，∠PDM的正、余弦值。所以sin ∠DME = √6/9，则cos ∠DME = ±√(1 - (√6/9)²) = ±5√3/9，因为0 ＜ λ ＜ 1，所以-√3/3 ＜ cos ∠DME ＜ 1，所以cos ∠DME = 5√3/9（负值舍去）。故在△PDM中，cos ∠PDM = (PD² + DM² - PM²)/(2PD × DM) = (12 + 6 - 2)/(2 × 2√3 × √6) = 2√2/3，则sin ∠PDM = 1/3。
第三步：根据两角和的正弦公式求得sin ∠DEM的值。在△EDM中，sin ∠DEM = sin(∠EDM + ∠DME) = sin ∠EDM cos ∠DME + cos ∠EDM sin ∠DME = (1/3) × (5√3/9) + (2√2/3) × (√6/9) = √3/3。
第四步：根据正弦定理求得λ的值。又DE = λDP = 2√3λ，所以在△EDM中，由正弦定理得DM/sin ∠DEM = DE/sin ∠DME，即√6/(√3/3) = 2√3λ/(√6/9)，解得λ = 1/3，所以λ的值为1/3。
解法三：
(1) 同解法一。
(2)(i) 同解法二。
(ii) 第一步：找出二面角D - BM - E的平面角，并求其余弦值的平方。因为BM ⊥平面ADP，DM，EM ⊂平面ADP，所以BM ⊥ DM，BM ⊥ EM，所以二面角D - BM - E的平面角为∠DME，所以sin ∠DME = √6/9，cos² ∠DME = 1 - (√6/9)² = 25/27。
第二步：在平面PAD内建立平面直角坐标系，并写出相关点及向量的坐标。在平面PAD内，以A为原点，分别以AP，AD的方向为x轴、y轴的正方向建立平面直角坐标系，如图所示，

则D(0, 2)，P(2√2, 0)，M(√2, 0)，DP = (2√2, -2)，MD = (-√2, 2)，DE = λDP = (2√2λ, -2λ)，ME = MD + DE = (2√2λ - √2, 2 - 2λ)。
第三步：利用向量的夹角公式求得λ的值。cos² ＜ME, MD＞ = ((ME · MD)/(|ME||MD|))² = (-4λ + 2 + 4 - 4λ)²/(6[(2√2λ - √2)² + (2 - 2λ)²]) = 25/27，化简得3λ² + 8λ - 3 = 0，解得λ = 1/3或λ = -3（舍去），所以λ的值为1/3。