《2026年高考基础卷物理》

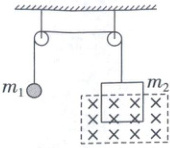
4. 回归教材 习题改编 如图所示，细线跨过两光滑定滑轮分别与质量为 $ m_1 $ 的小球和质量为 $ m_2 $ 的矩形线圈相连。线圈处于匀强磁场内，磁场方向垂直线圈平面向里，线圈的水平边长为 $ L $，当线圈通过恒定电流 $ I $ 时，整个装置处于静止状态。当电流反向后，线圈有向下的加速度，已知重力加速度为 $ g $，下列说法正确的是(D)


A.小球的质量大于线圈的质量
B.整个装置处于静止状态时电流沿顺时针方向
C.磁感应强度大小为 $ \dfrac{(m_1 + m_2)g}{IL} $
D.电流反向时，线圈的加速度大小为 $ \dfrac{2(m_2 - m_1)g}{m_1 + m_2} $

答案： 4. D 安培力 【解析】由题意可知，电流反向前，整个装置处于静止状态，电流反向后，线圈有向下的加速度，则电流反向前线圈受到安培力竖直向上，由左手定则可知，线圈中的电流沿逆时针方向，B 错误；装置处于静止状态时，对整个装置受力分析可得$m_1g = m_2g - BIL$，则$m_1 ＜ m_2$，磁感应强度大小$B = \frac{(m_2 - m_1)g}{IL}$，A、C 错误；电流反向后，线圈所受安培力竖直向下，小球和线圈加速度大小相同，对小球和线圈整体，由牛顿第二定律有$m_2g + BIL - m_1g = (m_1 + m_2)a$，联立解得$a = \frac{2(m_2 - m_1)g}{m_1 + m_2}$，D 正确。
教材溯源 本题由人教版选择性必修第二册 P7T3 改编，考点为安培力，该考点在真题中的考频为近 6 年 104 卷 11 考，教材原题以电流天平为情境，利用力的平衡，分析安培力的大小与方向，教材改编题将天平替换成滑轮组，根据线框的运动状态，分析安培力的大小和方向，进而求其他物理量，考查学生对所学知识的分析综合能力。

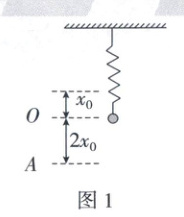
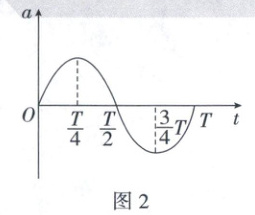
5. 如图 1 所示，一轻质弹簧上端固定，下端连接一质量为 $ m $ 的小球。初始时小球在 $ O $ 点静止，弹簧伸长量为 $ x_0 $，现把小球竖直向下拉至 $ O $ 点下方 $ 2x_0 $ 处的 $ A $ 点，静止释放后小球做简谐运动。忽略一切阻力，重力加速度为 $ g $。取竖直向上为正方向，从某时刻起开始计时，小球加速度随时间变化如图 2 所示，下列说法正确的是(B)


A.0 时刻，小球位于 $ A $ 点
B.$ \dfrac{T}{4} $ 时刻，小球与 $ O $ 相距 $ 2x_0 $
C.$ \dfrac{T}{2} $ 时刻，弹簧弹性势能为 0
D.$ \dfrac{3T}{4} $ 时刻，弹簧弹力大小为 $ 2mg $

答案： 5. B 弹簧振子
腾远·零障碍解题 信息提取
$t = \frac{T}{4}$时，加速度正向最大，说明小球处于最低点，$t = \frac{3T}{4}$时，小球处于最高点
$t = 0$时，加速度$a = 0$，说明小球处于平衡位置
$t = \frac{T}{2}$前后，加速度由正转负，说明小球由下向上经过平衡位置
【解析】由题图 2 可知，0 时刻小球加速度为 0，随时间沿正方向增大，所以小球正处于平衡位置$O$处且即将竖直向下运动，A 错误；$\frac{T}{4}$时刻小球加速度正向最大，可知小球正处于$A$点，与平衡位置$O$相距$2x_0$，B 正确；$\frac{T}{2}$时刻小球处于简谐运动最高点，由对称性可知，此时小球加速度和$A$点加速度大小相等，故弹簧处于压缩状态，由牛顿第二定律有$F_{弹} + mg = ma$，则$F_{弹} = mg$，D 错误；小球处于$O$点时，由力的平衡条件有$kx_0 = mg$，小球处于$A$点时，由牛顿第二定律有$3kx_0 - mg = ma$，解得加速度大小$a = 2g$，$\frac{3T}{4}$时刻小球处于简谐运动最高点，C 错误。

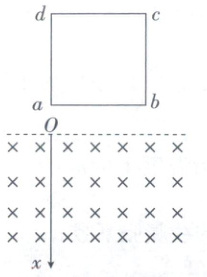
6. 如图所示，虚线下存在垂直纸面向里的磁场，以 $ O $ 点为坐标原点，竖直向下建立 $ x $ 轴，磁感应强度大小为 $ B = 4x $。一边长为 $ L $、电阻为 $ R $ 的正方形线框在磁场上方由静止释放，当线框的 $ cd $ 边进入磁场时，线框的速度大小为 $ v_0 $，重力加速度为 $ g $，此时给线框一个竖直向上的拉力 $ F = mg $，则线框从 $ cd $ 边刚进入磁场到达到平衡状态运动的位移为(C)


A.$ \dfrac{mv_0R}{2L^4} $
B.$ \dfrac{mv_0R}{8L^4} $
C.$ \dfrac{mv_0R}{16L^4} $
D.$ \dfrac{mv_0R}{32L^4} $

答案： 6. C 法拉第电磁感应定律、动量定理
腾远·零障碍解题 过程分解
线框的运动可分为以下两个过程：
过程 1——线框$ab$边进入磁场到$cd$边进入磁场，此过程线框中产生逆时针的感应电流，$ab$边所受安培力竖直向上，当$cd$边进入磁场时，对线框竖直向上的拉力等于线框的重力，这两个力平衡，线框在安培力的作用下做加速度减小的减速运动；
过程 2——线框完全进入磁场中，$ab$与$cd$边所处位置的磁感应强度差值不变，线框所受合外力仍为安培力，线框在安培力的作用下，继续做加速度减小的减速运动，直到速度为 0 达到平衡状态。对于整个过程，根据法拉第电磁感应定律、闭合电路欧姆定律和安培力公式列出线框所受安培力的合力表达式，再根据动量定理结合平均速度与时间乘积求解线框进入磁场后达到平衡状态时的位移。
【解析】线框完全进入磁场后，$ab$边和$cd$边所在位置磁感应强度大小始终相差$\Delta B = 4(x + L) - 4x = 4L$，则线圈中的感应电动势$\overline{E} = \Delta B L \overline{v} = 4L^2 \overline{v}$，由闭合电路欧姆定律可得感应电流$\overline{I} = \frac{\overline{E}}{R} = \frac{4L^2 \overline{v}}{R}$，线框所受安培力合力$\overline{F}_{安} = B_{ab}IL - B_{cd}IL = \frac{16L^4 \overline{v}}{R}$，由题可知，拉力和重力平衡，线框在安培力作用下在磁场中做减速运动，到达到平衡状态时速度为 0，由动量定理有$-\overline{F}_{安} t = 0 - mv_0$，即$\frac{16L^4 \overline{v}}{R} t = -mv_0$，$x = \overline{v} t$，解得线框从$cd$刚进入磁场到达到平衡状态运动的位移$x = \frac{mv_0 R}{16L^4}$，C 正确。