2026年高考基础卷物理
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年高考基础卷物理 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
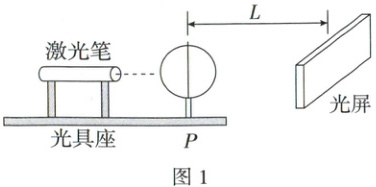
9. 方法新 用头发丝替代双缝 (8 分)某同学利用如图 1 的装置进行光学实验。
(1)在图 1 中的 $ P $ 处放置“单缝”,激光笔发出的单色光经过单缝后在光屏上看到的图案可能是

(2)该同学找到一根较粗且直径均匀的长头发,把头发不重叠的密绕在铅笔上。已知 100 匝的密绕头发长度为 $ l $,则头发的直径 $ d = $
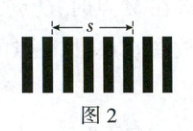
(3)把上述头发的一段粘贴在单缝的中心,使单缝成为双缝,双缝间距近似等于头发的直径,放置在图 1 中的 $ P $ 处,用激光笔照射双缝,在光屏上得到如图 2 所示条纹,则条纹间距为
(4)已知 $ P $ 与光屏的距离为 $ L $,则激光笔发射的激光的波长 $ \lambda = $
(1)在图 1 中的 $ P $ 处放置“单缝”,激光笔发出的单色光经过单缝后在光屏上看到的图案可能是
B
;
(2)该同学找到一根较粗且直径均匀的长头发,把头发不重叠的密绕在铅笔上。已知 100 匝的密绕头发长度为 $ l $,则头发的直径 $ d = $
$\frac{l}{100}$
;(3)把上述头发的一段粘贴在单缝的中心,使单缝成为双缝,双缝间距近似等于头发的直径,放置在图 1 中的 $ P $ 处,用激光笔照射双缝,在光屏上得到如图 2 所示条纹,则条纹间距为
$\frac{s}{4}$
;(4)已知 $ P $ 与光屏的距离为 $ L $,则激光笔发射的激光的波长 $ \lambda = $
$\frac{ls}{400L}$
。

答案:
9. (8分)
(1)B(2分)
(2)$\frac{l}{100}$(2分)
(3)$\frac{s}{4}$(2分)
(4)$\frac{ls}{400L}$(2分)
用双缝干涉装置测光的波长
【解析】
(1)光屏上看到的图案应为单缝衍射图样,单缝衍射中央亮条纹最宽,其余各级亮条纹和暗条纹的宽度大致相等,对称分布在中央亮条纹的两侧,B正确。
(2)$100$匝的密绕头发长度为$l$,则头发的直径$d=\frac{l}{100}$。
(3)由题图2可知,$s = 4\Delta x$,解得条纹间距$\Delta x=\frac{s}{4}$。
(4)由题可知,双缝间距等于头发的直径$d$,由双缝干涉条纹间距公式$\Delta x = L\frac{\lambda}{d}$可知,$\lambda=\frac{\Delta xd}{L}$,代入解得$\lambda=\frac{ls}{400L}$。
(1)B(2分)
(2)$\frac{l}{100}$(2分)
(3)$\frac{s}{4}$(2分)
(4)$\frac{ls}{400L}$(2分)
用双缝干涉装置测光的波长
【解析】
(1)光屏上看到的图案应为单缝衍射图样,单缝衍射中央亮条纹最宽,其余各级亮条纹和暗条纹的宽度大致相等,对称分布在中央亮条纹的两侧,B正确。
(2)$100$匝的密绕头发长度为$l$,则头发的直径$d=\frac{l}{100}$。
(3)由题图2可知,$s = 4\Delta x$,解得条纹间距$\Delta x=\frac{s}{4}$。
(4)由题可知,双缝间距等于头发的直径$d$,由双缝干涉条纹间距公式$\Delta x = L\frac{\lambda}{d}$可知,$\lambda=\frac{\Delta xd}{L}$,代入解得$\lambda=\frac{ls}{400L}$。
10. (12 分)如图所示为某 LED 灯玻璃体的结构图,其由半径为 $ R $ 的半圆柱 $ ABC $ 和厚为 $ 2R $ 的长方体 $ ACDE $ 组成。为研究该 LED 灯玻璃体的光学性能,将一束由 Ⅰ、Ⅱ 两种单色光组成的复色光以与 $ AE $ 面夹角为 $ 30° $ 照射到该玻璃体的 $ A $ 点,折射光线分别与半圆柱直径 $ AC $ 的夹角分别为 $ 45° $ 和 $ 30° $。已知真空中光速为 $ c $,不考虑光的反射。求:

(1)该玻璃体对单色光 Ⅰ 的折射率 $ n_1 $;
(2)单色光 Ⅱ 在玻璃体中的传播时间。

(1)该玻璃体对单色光 Ⅰ 的折射率 $ n_1 $;
(2)单色光 Ⅱ 在玻璃体中的传播时间。
答案:
10. (12分)
(1)$\frac{\sqrt{6}}{2}$
(2)$\frac{3R}{c}$
折射定律【解析】
(1)由题可知,复色光射向$AE$面的入射角为$i = 60^{\circ}$①(1分)
对单色光Ⅰ,折射角$r_{1}=45^{\circ}$,由折射定律有$n_{1}=\frac{\sin i}{\sin45^{\circ}}$②(1分)
解得$n_{1}=\frac{\sqrt{6}}{2}$③(2分)
(2)对单色光Ⅱ,折射角$r_{2}=30^{\circ}$,由折射定律有$n_{2}=\frac{\sin i}{\sin30^{\circ}}$④(1分)
解得$n_{2}=\sqrt{3}$⑤(1分)
单色光Ⅱ在玻璃中的传播速度$v=\frac{c}{n_{2}}$⑥(1分)
单色光Ⅱ在玻璃体中的传播路程$s = 2R\cos30^{\circ}$⑦(2分)
单色光Ⅱ在玻璃体中的传播时间$t=\frac{s}{v}$⑧(1分)
联立⑤⑥⑦⑧解得$t=\frac{3R}{c}$(2分)
技法链接 本题技法见《抢分必备》夺分妙技23/P22
(1)$\frac{\sqrt{6}}{2}$
(2)$\frac{3R}{c}$
折射定律【解析】
(1)由题可知,复色光射向$AE$面的入射角为$i = 60^{\circ}$①(1分)
对单色光Ⅰ,折射角$r_{1}=45^{\circ}$,由折射定律有$n_{1}=\frac{\sin i}{\sin45^{\circ}}$②(1分)
解得$n_{1}=\frac{\sqrt{6}}{2}$③(2分)
(2)对单色光Ⅱ,折射角$r_{2}=30^{\circ}$,由折射定律有$n_{2}=\frac{\sin i}{\sin30^{\circ}}$④(1分)
解得$n_{2}=\sqrt{3}$⑤(1分)
单色光Ⅱ在玻璃中的传播速度$v=\frac{c}{n_{2}}$⑥(1分)
单色光Ⅱ在玻璃体中的传播路程$s = 2R\cos30^{\circ}$⑦(2分)
单色光Ⅱ在玻璃体中的传播时间$t=\frac{s}{v}$⑧(1分)
联立⑤⑥⑦⑧解得$t=\frac{3R}{c}$(2分)
技法链接 本题技法见《抢分必备》夺分妙技23/P22
查看更多完整答案,请扫码查看


