《2026年高考基础卷物理》

7. 感动中国 2024 年度人物栾恩杰是中国首次月球探测工程总指挥，提出深空探测“探、登、驻（住）”和“绕、落、回”的技术发展路线。如图所示是月球探测器某次着陆的变轨过程，探测器首先在距离月球表面高度为 $h$ 的圆轨道 1 上稳定运行，运动周期为 $T$，为了实现月球软着陆，在 $A$ 点变轨进入椭圆轨道 2，$B$ 点为椭圆轨道的近月点，已知引力常量为 $G$，月球半径为 $R$。下列说法正确的是


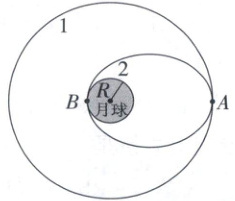
A.探测器在轨道 1 上 $A$ 点的速度大于在轨道 2 上 $A$ 点的速度
B.探测器在轨道 2 上从 $A$ 点到 $B$ 点的过程中，机械能逐渐增大
C.月球质量为 $\frac{4\pi^2(h + R)^3}{GT^2}$
D.探测器在轨道 2 上运动周期为 $\frac{\sqrt{2}}{4}T$

答案：
7.AC 万有引力定律、开普勒第三定律 【解析】卫星从高轨道变到低轨道需要减速，则探测器在轨道1上A点的速度大于在轨道2上A点的速度，A正确；探测器在轨道2上从A点到B点的过程中，只有万有引力做功，机械能不变，B错误；在A点，对探测器受力分析，根据万有引力提供向心力有$G\frac{Mm}{(h + R)^{2}} = m\frac{4\pi^{2}}{T^{2}}(h + R)$，解得月球质量$M = \frac{4\pi^{2}(h + R)^{3}}{GT^{2}}$，C正确；对探测器，根据开普勒第三定律有$\frac{r_{共}^{3}}{T_{2}^{2}} = \frac{(R + h)^{3}}{T^{2}}$，解得$T_{2} = (\frac{2R + h}{2R + 2h})^{\frac{3}{2}}T$，D错误。

腾远·零障碍解题 类题通法
椭圆轨道问题的处理技巧
1.在椭圆轨道上，卫星从远点向近点运动时，万有引力做正功，速度变大，加速度变大；从近点向远点运动时，万有引力做负功，速度变小，加速度变小。
2.椭圆轨道上运动的周期比低轨道周期大，比高轨道周期小，其周期的计算要根据开普勒第三定律，如图所示，$r$为低轨道半径，$R$为高圆轨道半径，椭圆轨道的半长轴为$\frac{R + r}{2}$，则有$\frac{T_{椭}^{2}}{T_{高}^{2}} = \frac{(\frac{R + r}{2})^{3}}{R^{3}}$。

8. 如图所示，竖直平面内存在两有界匀强电场，$MN$ 是两电场的分界线，分界线与水平方向的夹角 $\theta = 37°$，位于 $MN$ 左下方电场的电场强度大小为 $E_1$（未知），电场方向垂直于 $MN$，位于 $MN$ 右上方电场的电场强度大小 $E = \frac{mg}{q}$，电场方向竖直向下。一质量为 $m$、电荷量为 $+q$ 的带电小球从 $P$ 点由静止释放后，小球在 $E_1$ 中沿长度为 $l$ 的直线 $PQ$ 运动到 $Q$ 点后进入 $MN$ 右上方电场中。已知 $\sin37° = 0.6$，重力加速度为 $g$，则下列说法正确的是


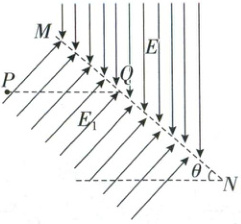
A.$MN$ 左下方电场强度 $E_1 = \frac{5mg}{4q}$
B.小球运动到 $Q$ 点的速度为 $\sqrt{2gl}$
C.小球在 $MN$ 右上方电场中运动的加速度大小为 $\sqrt{2g}$
D.小球在 $MN$ 右上方电场中运动的时间为 $\frac{3}{4}\sqrt{\frac{3l}{2g}}$

答案： 8.AD 带电体在电场、重力场的叠加场中的运动
【解析】由题可知，小球由静止释放后沿直线$PQ$运动，则小球所受合力方向沿水平方向，竖直方向受力平衡，对小球受力分析，沿竖直方向有$qE_{1}\cos37^{\circ} = mg$，解得$E_{1} = \frac{5mg}{4q}$，A正确；在左下方电场中，沿水平方向，对小球由牛顿第二定律有$qE_{1}\sin37^{\circ} = ma$，解得$a = \frac{3}{4}g$，从$P$点到$Q$点，由速度—位移公式有$v^{2} = 2al$，解得小球运动到$Q$点的速度为$v = \sqrt{\frac{3}{2}gl}$，B错误；由题可知，小球沿水平方向进入$MN$右上方电场，小球在右上方电场中做类平抛运动，设小球在右上方电场中运动的加速度大小、时间分别为$a_{1}$和$t$，由平抛运动规律可知，小球在水平方向位移满足$x = vt$，竖直方向位移满足$y = \frac{1}{2}a_{1}t^{2}$，沿竖直方向由牛顿第二定律有$Eq + mg = ma_{1}$，解得$a_{1} = 2g$，当小球返回$MN$时，结合几何关系有$\tan37^{\circ} = \frac{\frac{1}{2}a_{1}t^{2}}{vt}$，解得$t = \frac{3}{4}\sqrt{\frac{3l}{2g}}$，C错误，D正确。