《2026年期末直通车九年级数学全一册人教版》

1. (2024·新昌)如图, 在△ABC 中, AB = AC = 6, ∠BAC = 120°, 现以△ABC 的一条边为直径作圆, 所作的圆分别与△ABC 另外两条边所在的直线交于点 D,E(点 D,E 不与△ABC 的顶点重合), 则$\overgroup{DE}$的长为 (A)

A.$\sqrt{3}\pi$或 $2\pi$
B.$\sqrt{3}\pi$或 $\pi$
C.$2\sqrt{3}\pi$或 $2\pi$
D.$2\sqrt{3}\pi$或 $4\pi$

答案： 1.A 解析：①若以BA(或CA)为直径作圆，与直线BC交于点D，与直线CA(或BA)交于点E，则有圆心O到点D，E的长均为$\frac{1}{2}AB$，$\therefore$Rt$\triangle ABD$，Rt$\triangle ABE$，$\therefore AD$垂直平分BC，$\therefore \angle BAD=\frac{1}{2}\angle BAC=60°$，$\angle BAE=60°$，$\therefore l_{弦}=\frac{120}{180}· 3\pi=2\pi$。②若以BC为直径作圆，则易得$l_{弦}=\frac{120}{180}· 3\sqrt{3}\pi=\sqrt{3}\pi$。故选A。

2. (2024·温岭)已知⊙O 的直径 CD = 10 cm, AB 是⊙O 的弦, AB⊥CD, 垂足为 M, 且 AB = 8 cm, 则 AC 的长为 (C)

A.$2\sqrt{5}$ cm
B.$4\sqrt{5}$ cm
C.$4\sqrt{5}$ cm 或 $2\sqrt{5}$ cm
D.$2\sqrt{3}$ cm 或 $\sqrt{3}$ cm

答案：
2.C 解析：如图，连接AC，AO。$\because$⊙O的直径CD = 10 cm，AB⊥CD，AB = 8 cm，$\therefore$AM = $\frac{1}{2}$AB = 4(cm)，OD = OC = 5 cm。

①当点C的位置如图1所示时，$\because$OA = 5 cm，AM = 4 cm，CD⊥AB，$\therefore$OM = $\sqrt{OA^2 - AM^2}$ = $\sqrt{5^2 - 4^2}$ = 3(cm)，$\therefore$CM = OC + OM = 5 + 3 = 8(cm)，$\therefore$在Rt$\triangle AMC$中，AC = $\sqrt{AM^2 + CM^2}$ = $\sqrt{4^2 + 8^2}$ = 4$\sqrt{5}$(cm)。②当点C的位置如图2所示时，同理可得OM = 3 cm。$\because$OC = 5 cm，$\therefore$MC = 5 - 3 = 2(cm)，$\therefore$在Rt$\triangle AMC$中，AC = $\sqrt{AM^2 + CM^2}$ = $\sqrt{4^2 + 2^2}$ = 2$\sqrt{5}$(cm)。综上所述，AC的长为4$\sqrt{5}$cm或2$\sqrt{5}$cm。故选C。

3. (2024·玉环)已知二次函数 $y = x^2 - 2ax + a^2 - 1$, 当 $-1 \leq x \leq 2$时, 函数的最大值与最小值的差为 3, 则 a 的值为 (C)

A.1 或 0
B.1 或 $2 - \sqrt{3}$
C.$2 - \sqrt{3}$或 $\sqrt{3} - 1$
D.0 或 $\sqrt{3} - 1$

答案： 3.C 解析：$\because y=(x - a)^2 - 1$，$\therefore$函数图象的对称轴为直线x = a，当x = -1时，y = $(a + 1)^2 - 1$；当x = 2时，y = $(2 - a)^2 - 1$。①当$a ＞ 2$时，$(a + 1)^2 - 1 - [(2 - a)^2 - 1] = 3$，解得a = 1，与$a ＞ 2$矛盾，舍去；②当$\frac{-1 + 2}{2} ＜ a \leq 2$时，有$(a + 1)^2 - 1 - (-1) = 3$，解得$a = \pm\sqrt{3} - 1$，$\because\frac{1}{2} ＜ a \leq 2$，$\therefore a = \sqrt{3} - 1$；③当$-1 ＜ a \leq\frac{1}{2}$时，有$(2 - a)^2 - 1 - (-1) = 3$，解得$a = \pm\sqrt{3} + 2$，$\because -1 ＜ a \leq\frac{1}{2}$，$\therefore a = 2 - \sqrt{3}$；④当$a \leq -1$时，有$(2 - a)^2 - 1 - [(a + 1)^2 - 1] = 3$，解得a = 0，这与$a \leq -1$矛盾，舍去。综上，$a = \sqrt{3} - 1$或$2 - \sqrt{3}$。故选C。

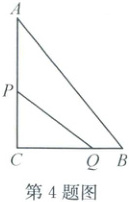
4. (2024·绍兴上虞)如图, 在 Rt△ABC 中, ∠C = 90°, AC = 10 cm, BC = 8 cm. 点 P 从点 C 出发, 以 2 cm/s 的速度沿着 CA 向点 A 匀速运动, 同时点 Q 从点 B 出发, 以 1 cm/s 的速度沿着 BC 向点 C 匀速运动, 当一个点到达终点时, 另一个点随之停止运动, 经过$\frac{40}{13}$或$\frac{16}{7}$ s, △PCQ 与△ABC 相似.

答案： 4.$\frac{40}{13}$或$\frac{16}{7}$ 解析：设时间为t s，则BQ = t cm，CP = 2t cm，CQ = (8 - t)cm，①若$\triangle PCQ\sim\triangle ACB$，则$\frac{PC}{AC}=\frac{CQ}{CB}$，即$\frac{2t}{10}=\frac{8 - t}{8}$，解得$t = \frac{40}{13}$；②若$\triangle PCQ\sim\triangle BCA$，则$\frac{PC}{BC}=\frac{CQ}{CA}$，即$\frac{2t}{8}=\frac{8 - t}{10}$，解得$t = \frac{16}{7}$。综上所述，经过$\frac{40}{13}$s或$\frac{16}{7}$s，$\triangle PCQ$与$\triangle ABC$相似。