《2026年期末直通车九年级数学全一册人教版》

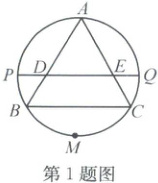
1. (2024·三门)如图，把正△ABC 的外接圆对折，使点 A 与$\overset{\frown}{BC}$的中点 M 重合，若折痕 PQ 的长为 6，则折痕在△ABC 内的部分 DE 的长为(A)

A.$2\sqrt{3}$
B.$\sqrt{3}$
C.4
D.3

答案：
1.A 解析：连接AM与PQ交于点O，$\because AB=AC$，$\therefore\widehat{AB}=\widehat{AC}$，又$\because BM=CM$，$\therefore\widehat{ABM}=\widehat{ACM}$，$\therefore AM$为直径，又$\because$点A与点M重合，$\therefore PQ$为直径，$\therefore$点O为圆心，$\therefore$易得$OA=OQ=\frac{1}{2}PQ=3$，且易证$\triangle ADE$为正三角形，$\therefore DE=2\sqrt{3}$.故选A.

2. (2024·嘉兴)如图，AB 是⊙O 的一条弦，将劣弧沿弦 AB 翻折，连接 AO 并延长交翻折后的弧于点 C，连接 BC，若 AB = 2，BC = 1，则 AC 的长为(C)

A.$\frac{2}{3}\sqrt{5}$
B.$\frac{3}{4}\sqrt{5}$
C.$\frac{3}{5}\sqrt{5}$
D.$\frac{5}{7}\sqrt{5}$

答案：
2.C 解析：如图，在未翻折前取一点$C^{\prime}$，使$AC=AC^{\prime}$，连接$AC^{\prime}$，$BC^{\prime}$，并延长AC，交$\odot O$于点D，连接BD，再过点B作$BH\perp AD$，H为垂足，则易得$\angle CAB=\angle DAB$，$\therefore BC=BC^{\prime}=BD$，且由AD为直径，得$\angle ABD=90^{\circ}$，$\therefore$在$Rt\triangle ABD$中，$AB=2$，$BD=1$，$AD=\sqrt{5}$.设$DH=x$，则$AH=\sqrt{5}-x$，$\therefore BH^{2}=4-(\sqrt{5}-x)^{2}=1-x^{2}$.解得$x=\frac{\sqrt{5}}{5}$.$\therefore AC=AD-DC=\sqrt{5}-2x=\sqrt{5}-\frac{2}{5}\sqrt{5}=\frac{3}{5}\sqrt{5}$.故选C.

3. (2024·宁波海曙)如图，△ABC 内接于半径为$\sqrt{5}$的半圆 O，AB 为直径，M 是$\overset{\frown}{AC}$的中点，连接 BM 交 AC 于点 E，AD 平分∠CAB 交 BM 于点 D，且 D 为 BM 的中点，则 BC 的长为(C)

A.$\frac{6\sqrt{10}}{5}$
B.$\frac{3\sqrt{10}}{5}$
C.$\frac{6\sqrt{5}}{5}$
D.$\frac{3\sqrt{5}}{5}$

答案：
3.C 解析：如图，过点M作$MH\perp AB$，H为垂足，并连接AM，OM，并记OM与AC交点为F，由题意$AM=CM$，得$\angle ABM=\angle CBM$，又$\because$AD平分$\angle CAB$，$\therefore$易得$\angle ADB=180^{\circ}-\frac{1}{2}(\angle ABC+\angle BAC)=135^{\circ}$，$\therefore\angle ADM=45^{\circ}$.设$AM=a$，则$BM=2a$，$\therefore$在$Rt\triangle AMB$中有$a^{2}+4a^{2}=20$.解得$a=2$，即$AM=2$，$BM=4$，$\therefore MH=\frac{AM· BM}{AB}=\frac{4}{5}\sqrt{5}$，$\therefore OH=\sqrt{OM^{2}-MH^{2}}=\frac{3}{5}\sqrt{5}$，又易证$\triangle AOF\cong\triangle MOH$，$\therefore OF=OH=\frac{3}{5}\sqrt{5}$，$\therefore BC=2OF=\frac{6}{5}\sqrt{5}$.故选C.

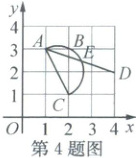
4. (2024·杭州拱墅)如图，在平面直角坐标系中，一段圆弧过点 A(1,3)，点 B(2,3)，点 C(2,1)，以点 A 和点 D(4,2)为端点的线段与该圆弧相交于点 E，则$\overset{\frown}{CE}$的长为$\frac{\sqrt{5}}{4}\pi$.

答案：
4.$\frac{\sqrt{5}}{4}\pi$ 解析：如图，取AC中点T，连接ET，CD.$\because\angle ABC=90^{\circ}$，$\therefore AC$为直径，$\therefore T$为$\overset{\frown}{CE}$所在圆的圆心，$\because AC=CD=\sqrt{1^{2}+2^{2}}=\sqrt{5}$，$AD=\sqrt{1^{2}+3^{2}}=\sqrt{10}$，$\therefore AC^{2}+CD^{2}=AD^{2}$，$\therefore\angle ACD=90^{\circ}$，$\therefore\angle CAD=45^{\circ}$，$\therefore\angle ETC=2\angle CAD=90^{\circ}$.$\because TC=ET=TA=\frac{\sqrt{5}}{2}$，$\therefore l_{\overset{\frown}{CE}}=\frac{90\pi×\frac{\sqrt{5}}{2}}{180}=\frac{\sqrt{5}}{4}\pi$.

5. (2024·绍兴柯桥)如图，AB 是半圆的直径，BC 是半圆的弦，BC = $4\sqrt{5}$，弧 BC 沿弦 BC 折叠交直径 AB 于点 D，此时 BD = 6，则 AD 的长为4.

答案：
5.4 解析：如图，记点D关于BC的对称点为$D^{\prime}$，并连接$CD^{\prime}$，$BD^{\prime}$，CA，CD，再过点C作$CH\perp AB$，H为垂足，则易知点$D^{\prime}$在圆上，$\therefore$由$\angle ABC=\angle D^{\prime}BC$，得$AC=D^{\prime}C$，$\therefore AC=DC$.设$AD=x$，则$AH=\frac{x}{2}$，$HB=\frac{x}{2}+6$，$AB=x+6$，易证$\triangle CHB\backsim\triangle ACB$，$\therefore\frac{CB}{AB}=\frac{HB}{CB}$，即$CB^{2}=AB· HB$，$\therefore$有$80=(x+6)·(\frac{x}{2}+6)$，解得$x=4$或$-22$(舍去).$\therefore AD$的长为4.