《2026年期末直通车九年级数学全一册人教版》

5. (2024·杭州拱墅)如图,将矩形ABCD绕点A逆时针旋转90°得到矩形AB'C'D',若点C,B',D'恰好在同一直线上,且BC=2,则AB的长为√3.

答案：
5.$\sqrt{3}$　解析:如图，连接$CF$，易证$\triangle FCD$为等边三角形，又易知在$\triangle CBD$中$\angle CDB = \angle DCB = 30^{\circ}$，$\therefore FC \perp AB$，设$CB = x$，则$AC = 8 - x$，$FC = CD = \sqrt{3}x$，$\therefore AF^{2} = AC^{2} + FC^{2} = (8 - x)^{2} + (\sqrt{3}x)^{2} = 4x^{2} - 16x + 64 = 4(x - 2)^{2} + 48(0 \leq x \leq 8)$。易知当$x = 2$时，$AF^{2}$有最小值，即$AF$有最小值。此时$S_{\triangle BCD} = \frac{1}{2} × 2 × \sqrt{3} = \sqrt{3}$。

6. (2024·乐清)如图,线段AB=8,C是线段AB上的动点,将线段BC绕点B顺时针旋转120°得到线段BD,连接CD,在AB的上方作Rt△DCE,使∠DCE=90°,∠E=30°,F为DE的中点,连接AF,当AF最小时,△BCD的面积为.

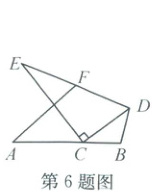
答案： √3

7. (2024·龙游、江山、开化)如图,E为正方形ABCD的对角线AC上一点,连接DE,将DE所在直线绕点D逆时针旋转45°,交对角线AC于点F,交边BC于点G.已知∠CDG=α,CB=4CG=4.则:
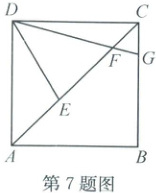
(1)∠DEC=90°-α(用含α的代数式表示).
(2)CE·CF=4.

答案：
7.
(1)$90^{\circ} - \alpha$　
(2)4　解析:
(1)在$\triangle DEC$中，$\angle CDG = \alpha$，$\angle DCE = \angle EDF = 45^{\circ}$，$\therefore \angle DEC = 180^{\circ} - \angle EDF - \angle CDG - \angle DCE = 90^{\circ} - \alpha$。
(2)如图，连接$BD$，交$AC$于点$O$。易证$\triangle DEO \sim \triangle DGC$，$\therefore \frac{DO}{OE}=\frac{DC}{CG}=4$，又易得$DO = CO = 2\sqrt{2}$，$\therefore EO = \frac{\sqrt{2}}{2}$，$\therefore CE = \frac{5}{2}\sqrt{2}$。又$\because$在$Rt\triangle DCG$中，$CF$平分$\angle DCG$，由点$F$分别向$DC$，$CG$作垂线，由等面积法，可得$DC · CG = DC · \frac{\sqrt{2}}{2}CF + CG · \frac{\sqrt{2}}{2}CF$，$\therefore CF = \sqrt{2} × \frac{4 × 1}{4 + 1}=\frac{4}{5}\sqrt{2}$，$\therefore CE · CF = \frac{5}{2}\sqrt{2} × \frac{4}{5}\sqrt{2} = 4$。

8. (2024·新昌)有两块等腰直角三角尺如图1放置,将三角尺BDE绕着点B在同一平面顺时针方向旋转.如图2,连接AE,分别取AE,BD的中点G,F,并连接CG,GF,CF.已知∠ACB=∠DEB=90°,AC=BC=7,DE=BE=3√2,在三角尺BDE旋转一周的过程中,△CGF的最大面积是25.

答案：
8.25　解析:如图，延长$AC$至点$M$，使$MC = AC$，并连接$BM$，$EM$，$EF$，再延长$EF$至点$N$，使$NF = EF$，连接$BN$，$AN$，易证$\triangle MEB \cong \triangle ANB$，$\therefore \angle EMB = \angle NAB$，$ME = AN$，$\therefore$易得$ME \perp AN$。又$\because G$，$C$，$F$分别为$AE$，$AM$，$EN$中点，$\therefore CG // \frac{1}{2}ME$，$GF // \frac{1}{2}AN$，$\therefore CG = GF$，且$CG \perp GF$，$\therefore S_{\triangle CGF} = \frac{1}{2}CG^{2} = \frac{1}{2}(\frac{1}{2}ME)^{2} = \frac{1}{8}ME^{2}$。又$\because ME \leq MB + BE = 7\sqrt{2} + 3\sqrt{2} = 10\sqrt{2}$，$\therefore S_{\triangle CGF} = \frac{1}{8}ME^{2} \leq \frac{1}{8}(10\sqrt{2})^{2} = 25$，$S_{\triangle CGF}$的最大值为25。

9. (2024·杭州拱墅)借助三角形的中位线可构造一组相似三角形,若将它们绕公共顶点旋转,对应顶点连线的长度存在特殊的数量关系,数学小组对此进行了研究.如图1,在△ABC中,∠B=90°,AB=BC=4,分别取AB,AC的中点D,E,连接DE.如图2所示,将△ADE绕点A逆时针旋转,连接BD,CE.
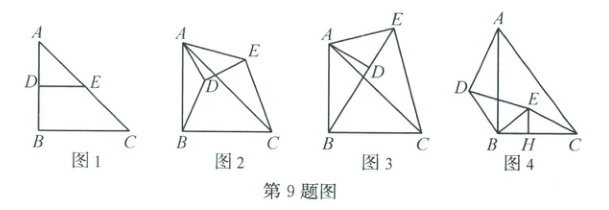
(1)旋转过程中,线段BD和CE的长度存在怎样的数量关系?写出你的猜想,并证明.
(2)如图3,旋转过程中,当DE所在直线首次经过点B时,求CE的长.
(3)在Rt△ABC中,∠ABC=90°,AB=8,BC=6,分别取AB,BC的中点D,E,连接DE,将△BDE绕点B逆时针旋转,再过点E作EH⊥BC,H为垂足,并连接AD,CE.如图4,当边AB平分线段DE时,求$\frac{EH}{HC}$的值.

答案：
三、9.解:
(1)$CE = \sqrt{2}BD$　证明如下:$\because \angle B = 90^{\circ}$，$AB = BC$，$\therefore AC = \sqrt{2}AB$。$\because \angle DAE = \angle BAC$，$\therefore \angle BAD = \angle CAE$，$\because \frac{AD}{AB}=\frac{AE}{AC}=\frac{1}{2}$，$\therefore \triangle ABD \sim \triangle ACE$，$\therefore \frac{CE}{BD}=\frac{AC}{AB}=\sqrt{2}$，$\therefore CE = \sqrt{2}BD$。
(2)由
(1)易得:$\triangle ABD \sim \triangle ACE$，$\therefore \angle AEC = \angle ADB = \angle ADE = 90^{\circ}$，$\therefore \angle AEC + \angle ABC = 180^{\circ}$，$\therefore$点$A$，$B$，$C$，$E$共圆，$\therefore \angle BEC = \angle BAC = 45^{\circ}$，$\because \angle ABC = \angle ADB = \angle AEC = 90^{\circ}$，$AB = 4$，$AD = 2$，$\therefore AE = \sqrt{2}AD = 2\sqrt{2}$，$\therefore CE = \sqrt{AC^{2}-AE^{2}} = 2\sqrt{6}$。
(3)设$AB$与$DE$相交于点$Q$，
如图，易得$\triangle DBE \sim \triangle ABC$，$\therefore \angle BED = \angle BCA$，$\angle DBE = \angle ABC = 90^{\circ}$。$\because AB$平分$DE$，$\therefore DQ = QE$，$\therefore BQ = EQ = \frac{1}{2}DE$，$\therefore \angle ABE = \angle DEB = \angle ACB$。
$\because \angle ABE + \angle CBE = 90^{\circ}$，$\angle CBE + \angle BEH = 90^{\circ}$，$\therefore \angle ABE = \angle BEH$，$\therefore \angle BEH = \angle ACB$，$\therefore BH = BE · \sin\angle BEH = 3×\frac{4}{5}=\frac{12}{5}$，$EH = BE · \cos\angle BEH = 3×\frac{3}{5}=\frac{9}{5}$，$\therefore HC = BC - BH = 6 - \frac{12}{5}=\frac{18}{5}$，$\therefore \frac{EH}{HC}=\frac{1}{2}$。