《2025年人教金学典同步解析与测评八年级数学上册人教版云南专版》

18. 在$\triangle ACD与\triangle BCE$中,$AD与BE$,$CE分别相交于点P$,$F$,如图所示.若$AC = BC$,$AD = BE$,$CD = CE$,$\angle ACE = 55^{\circ}$,$\angle BCD = 155^{\circ}$,则$\angle BPD$的度数为______.

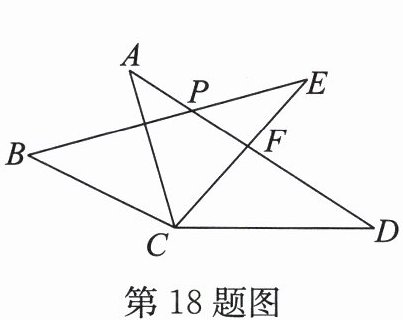
答案： 130°

19. 如图,在平面直角坐标系中,$C(6,6)$,点$B$,$A分别在x轴正半轴和y$轴正半轴上,$\angle ACB = 90^{\circ}$,则$OA + OB$等于______.

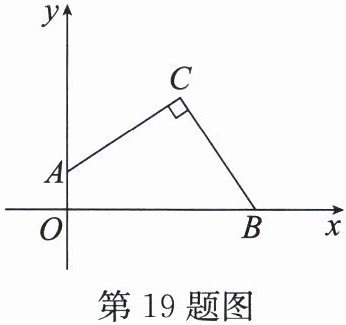
答案： 12

20. (6 分)如图,在$\triangle AFD和\triangle CEB$中,点$A$,$E$,$F$,$C$在同一条直线上,$AE = CF$,$\angle B = \angle D$,$AD // BC$.求证：$AD = BC$.

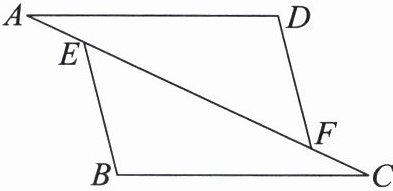
答案： 证明:因为AE=CF，所以AF=CE.因为AD//BC，所以∠A=∠C.在△AFD和△CEB中，∠A=∠C，∠B=∠D，AF=CE，所以△AFD≌△CEB(AAS).所以AD=BC.

21. (7 分)如图,$AB = AC$,$AD \perp BC于点D$,$AD = AE$,$AB平分\angle DAE交DE于点F$,连接$BE$.请你写出图中三对全等三角形,并选取其中一对加以证明.

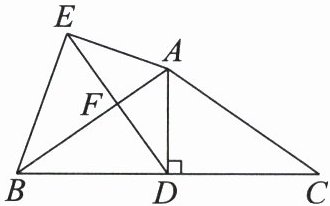
答案： 解:△ABD≌△ACD,△AEF≌△ADF,△AEB≌△ADB(答案不唯一).选取△ABD≌△ACD.证明如下:因为AD⊥BC，所以∠ADB=∠ADC=90°.在Rt△ABD和Rt△ACD中，AB=AC，AD=AD，所以Rt△ABD≌Rt△ACD(HL).

22. (7 分)如图,利用尺规,在$\triangle ABC的边AC上方作\angle CAE = \angle ACB$,在射线$AE上截取AD = BC$,连接$CD$,并证明$AB // CD$.(尺规作图要求保留作图痕迹,不写作法)

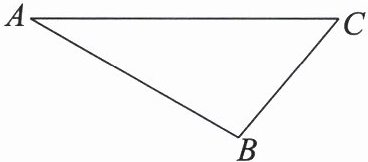
答案：
解:如图所示. 证明:因为∠CAE=∠ACB,AD=BC,AC=CA，所以△ACD≌△CAB(SAS).所以∠ACD=∠CAB，所以AB//CD.

23. (7 分)如图,已知在长方形$ABCD$中,$F是BC$上一点,且$AF = BC$,$DE \perp AF于点E$,连接$DF$.
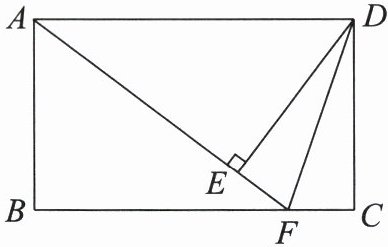
求证：(1)$\triangle ABF \cong \triangle DEA$；
(2)$DF是\angle EDC$的平分线.

答案： 证明:
(1)因为AF=BC,BC=AD,所以AF=AD.因为DE⊥AF,∠B=90°，所以∠B=∠AED.因为AD//CB，所以∠AFB=∠DAE.在△ABF和△DEA中，∠B=∠AED，∠AFB=∠DAE，AF=DA，所以△ABF≌△DEA(AAS).
(2)由
(1),得AE=BF,所以AF - AE=BC - BF,即FE=FC.因为DE⊥AF,DC⊥CF，所以DF是∠EDC的平分线.

24. (8 分)如图,在$\triangle ABC和\triangle AED$中,$AB = AC$,$AE = AD$,$\angle BAC = \angle EAD$,且点$E$,$A$,$B$在同一条直线上,点$C$,$D在EB$的同侧,连接$BD$,$CE交于点M$.
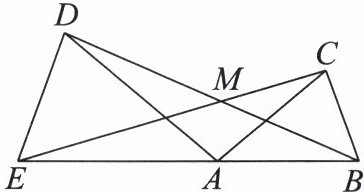
(1)求证：$\triangle ABD \cong \triangle ACE$.
(2)若$\angle CAD = 100^{\circ}$,求$\angle DME$的度数.

答案：
(1)证明:因为∠BAC=∠EAD，所以∠BAC+∠DAC=∠EAD+∠DAC,即∠DAB=∠EAC.在△ABD和△ACE中，AD=AE，∠DAB=∠EAC，AB=AC，所以△ABD≌△ACE(SAS).
(2)解:因为∠BAC=∠EAD,∠CAD=100°，所以∠BAC=∠EAD=40°.因为∠BAC是△EAC的一个外角，所以∠BAC=∠AEC+∠ACE=40°.因为△ABD≌△ACE，所以∠ECA=∠DBA.因为∠DME是△BME的一个外角，所以∠DME=∠AEC+∠ABD=∠AEC+∠ACE=40°.