27. (12分)学习了“平方差公式”和“完全平方公式”后,灵活运用乘法公式往往能化繁为简,巧妙解题.
【初步尝试】
(1) 已知 $ x^{2}+y^{2}= (x+y)^{2}-P= (x-y)^{2}+Q $,则 $ P= $ ______, $ Q= $ ______.
【灵活运用】
(2) 由(1)可知, $ a+b,a-b,a^{2}+b^{2},ab $ 这四个代数式之间具有一定的关系.
例如,当 $ a,b $ 为正数时,如果 $ a-b= 3,ab= 10 $,那么 $ (a+b)^{2}= (a-b)^{2}+ $ ______,所以 $ a+b= $ ______.
(3) 已知长和宽分别为 $ a,b $ 的长方形,它的周长为22,面积为30,如图所示,求 $ a^{2}+b^{2}-ab $ 的值.

【解决问题】
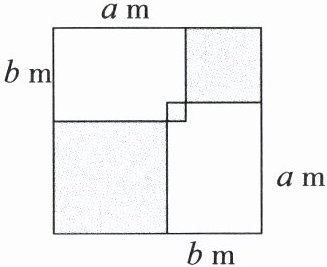
(4) 某学校“行知农场”开辟出一块边长为11 m的正方形菜地,计划种植黄瓜与西红柿两种蔬菜. 兼顾美观,在菜地中设计两个长和宽分别为 $ a $ m, $ b $ m 的长方形,其中每个长方形的长与宽之差为2 m,每个长方形的面积为 $ 35 m^{2} $,如图所示,计划在图中阴影部分种植黄瓜,其余菜地种植西红柿,请求出黄瓜的种植面积.
【初步尝试】
(1) 已知 $ x^{2}+y^{2}= (x+y)^{2}-P= (x-y)^{2}+Q $,则 $ P= $ ______, $ Q= $ ______.
【灵活运用】
(2) 由(1)可知, $ a+b,a-b,a^{2}+b^{2},ab $ 这四个代数式之间具有一定的关系.
例如,当 $ a,b $ 为正数时,如果 $ a-b= 3,ab= 10 $,那么 $ (a+b)^{2}= (a-b)^{2}+ $ ______,所以 $ a+b= $ ______.
(3) 已知长和宽分别为 $ a,b $ 的长方形,它的周长为22,面积为30,如图所示,求 $ a^{2}+b^{2}-ab $ 的值.

【解决问题】
(4) 某学校“行知农场”开辟出一块边长为11 m的正方形菜地,计划种植黄瓜与西红柿两种蔬菜. 兼顾美观,在菜地中设计两个长和宽分别为 $ a $ m, $ b $ m 的长方形,其中每个长方形的长与宽之差为2 m,每个长方形的面积为 $ 35 m^{2} $,如图所示,计划在图中阴影部分种植黄瓜,其余菜地种植西红柿,请求出黄瓜的种植面积.

答案:
解:【初步尝试】
(1)因为$x^{2}+y^{2}=(x+y)^{2}-P,$所以$P=(x+y)^{2}-(x^{2}+y^{2})$$=x^{2}+2xy+y^{2}-x^{2}-y^{2}=2xy.$因为$x^{2}+y^{2}=(x-y)^{2}+Q,$所以$Q=(x^{2}+y^{2})-(x-y)^{2}$$=x^{2}+y^{2}-x^{2}+2xy-y^{2}=2xy.$故答案为 2xy;2xy.【灵活运用】
(2)由
(1)可知$(a+b)^{2}=(a-b)^{2}+4ab.$因为$a-b=3,ab=10,$所以$(a+b)^{2}=3^{2}+4×10=49.$因为 a,b 为正数,所以$a+b=7.$故答案为 4ab;7.
(3)由长和宽分别为 a,b 的长方形,它的周长为 22,面积为 30,可知$2(a+b)=22,$$ab=30,$所以$a+b=11,$所以$a^{2}+b^{2}-ab=(a+b)^{2}-3ab=11^{2}-3×30=31.$
(4)由题意,得$\left\{\begin{array}{l} a-b=2,\\ ab=35,\end{array}\right. $所以$(a+b)^{2}=(a-b)^{2}+4ab=2^{2}+4×35=144,$所以$a+b=12,$所以阴影部分的面积为$(11-a)^{2}+(11-b)^{2}+(a+b-11)^{2}$$=a^{2}+b^{2}-22(a+b)+242+(a+b-11)^{2}$$=(a+b)^{2}-2ab-22(a+b)+242+(a+b-11)^{2}$$=144-2×35-22×12+242+(12-11)^{2}$$=53(m^{2}).$所以黄瓜的种植面积为$53m^{2}.$
(1)因为$x^{2}+y^{2}=(x+y)^{2}-P,$所以$P=(x+y)^{2}-(x^{2}+y^{2})$$=x^{2}+2xy+y^{2}-x^{2}-y^{2}=2xy.$因为$x^{2}+y^{2}=(x-y)^{2}+Q,$所以$Q=(x^{2}+y^{2})-(x-y)^{2}$$=x^{2}+y^{2}-x^{2}+2xy-y^{2}=2xy.$故答案为 2xy;2xy.【灵活运用】
(2)由
(1)可知$(a+b)^{2}=(a-b)^{2}+4ab.$因为$a-b=3,ab=10,$所以$(a+b)^{2}=3^{2}+4×10=49.$因为 a,b 为正数,所以$a+b=7.$故答案为 4ab;7.
(3)由长和宽分别为 a,b 的长方形,它的周长为 22,面积为 30,可知$2(a+b)=22,$$ab=30,$所以$a+b=11,$所以$a^{2}+b^{2}-ab=(a+b)^{2}-3ab=11^{2}-3×30=31.$
(4)由题意,得$\left\{\begin{array}{l} a-b=2,\\ ab=35,\end{array}\right. $所以$(a+b)^{2}=(a-b)^{2}+4ab=2^{2}+4×35=144,$所以$a+b=12,$所以阴影部分的面积为$(11-a)^{2}+(11-b)^{2}+(a+b-11)^{2}$$=a^{2}+b^{2}-22(a+b)+242+(a+b-11)^{2}$$=(a+b)^{2}-2ab-22(a+b)+242+(a+b-11)^{2}$$=144-2×35-22×12+242+(12-11)^{2}$$=53(m^{2}).$所以黄瓜的种植面积为$53m^{2}.$
查看更多完整答案,请扫码查看


