《2025年人教金学典同步解析与测评八年级数学上册人教版云南专版》

24. (8分)下面是小颖对多项式因式分解的过程,请认真阅读并完成相应问题.
分解因式:$(3x+y)^{2}-(x+3y)^{2}$.
解:原式$=(3x+y+x+3y)(3x+y-x-3y)……$第一步
$=(4x+4y)(2x-2y)……$第二步
$=8(x+y)(x-y)……$第三步
$=8(x^{2}-y^{2})……$第四步
(1)以上变形过程中,第一步依据的公式用字母$a,b$表示为____;
(2)以上分解过程第____步出现错误,具体错误为____;
(3)请写出正确的解题过程.

答案： 解:
(1)$a^{2}-b^{2}=(a+b)(a-b)$
(2)四 进行了乘法运算
(3)原式$=(3x+y+x+3y)(3x+y-x-3y)$
$=(4x+4y)(2x-2y)$
$=8(x+y)(x-y)$.

25. (8分)如图(单位:cm),将一张长方形纸板按图中虚线裁剪成九块,其中有两块是边长都为$m$ cm的大正方形,两块是边长都为$n$ cm的小正方形,五块是长为$m$ cm,宽为$n$ cm的全等小长方形,且$m＞n$.

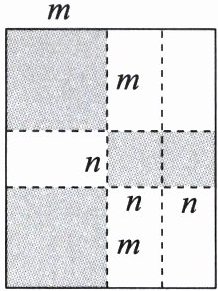
(1)观察图形,可以发现代数式$2m^{2}+5mn+2n^{2}$可以因式分解为____;
(2)若每块小长方形的面积为$10$ cm^2,两个大正方形和两个小正方形的面积和为$58$ cm^2,试求$m+n$的值.

答案： 解:
(1)$(2m+n)(m+2n)$
(2)$m+n=7$.