25. (8 分)如图,在△ABC 中,∠ACB= 90°,∠ABC= 30°,AD 平分∠CAB,延长 AC 至点 E,使 CE= AC。
(1)求证:DE= DB;
(2)连接 BE,试判断△ABE 的形状,并说明理由。
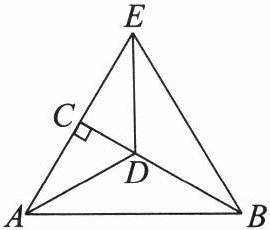
(1)求证:DE= DB;
(2)连接 BE,试判断△ABE 的形状,并说明理由。

答案:
(1)证明:因为∠ACB=90°,∠ABC=30°,所以BC⊥AE,∠CAB=60°.
因为AD平分∠CAB,
所以∠DAB=$\frac{1}{2}$∠CAB=30°=∠ABC,所以DA=DB.
因为CE=AC,
所以BC是线段AE的垂直平分线,
所以DE=DA,所以DE=DB.
(2)解:△ABE是等边三角形.理由如下:因为BC是线段AE的垂直平分线,
所以BA=BE,
即△ABE是等腰三角形.
又因为∠CAB=60°,
所以△ABE是等边三角形.
(1)证明:因为∠ACB=90°,∠ABC=30°,所以BC⊥AE,∠CAB=60°.
因为AD平分∠CAB,
所以∠DAB=$\frac{1}{2}$∠CAB=30°=∠ABC,所以DA=DB.
因为CE=AC,
所以BC是线段AE的垂直平分线,
所以DE=DA,所以DE=DB.
(2)解:△ABE是等边三角形.理由如下:因为BC是线段AE的垂直平分线,
所以BA=BE,
即△ABE是等腰三角形.
又因为∠CAB=60°,
所以△ABE是等边三角形.
26. (8 分)如图,在△ABC 中,AB= AC,D 是 BC 边上的中点,连接 AD,BE 平分∠ABC 交 AC 于点 E,过点 E 作 EF//BC 交 AB 于点 F。
(1)若∠C= 36°,求∠BAD 的度数。
(2)求证:FB= FE。
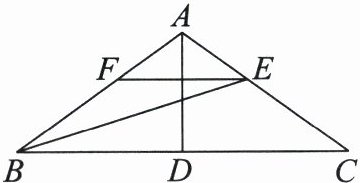
(1)若∠C= 36°,求∠BAD 的度数。
(2)求证:FB= FE。

答案:
(1)解:因为AB=AC,
所以∠C=∠ABC.
因为∠C=36°,
所以∠ABC=36°.
因为AB=AC,D是BC边上的中点,
所以AD⊥BC,
所以∠ADB=90°,
所以∠BAD=90°-36°=54°.
(2)证明:因为BE平分∠ABC,
所以∠ABE=∠CBE=$\frac{1}{2}$∠ABC.
因为EF//BC,
所以∠FEB=∠CBE,
所以∠FBE=∠FEB,
所以FB=FE.
(1)解:因为AB=AC,
所以∠C=∠ABC.
因为∠C=36°,
所以∠ABC=36°.
因为AB=AC,D是BC边上的中点,
所以AD⊥BC,
所以∠ADB=90°,
所以∠BAD=90°-36°=54°.
(2)证明:因为BE平分∠ABC,
所以∠ABE=∠CBE=$\frac{1}{2}$∠ABC.
因为EF//BC,
所以∠FEB=∠CBE,
所以∠FBE=∠FEB,
所以FB=FE.
27. (12 分)(1)问题发现:
如图①,△ACB 和△DCE 均为等边三角形,点 A,D,E 在同一直线上,连接 BE。
①∠AEB 的度数为______;
②线段 AD,BE 之间的数量关系是______。
(2)拓展探究:
如图②,△ACB 和△DCE 均为等腰三角形,∠ACB= ∠DCE= 90°,点 A,D,E 在同一直线上,CM 为△DCE 中 DE 边上的高,连接 BE。请判断∠AEB 的度数及线段 CM,AE,BE 之间的数量关系,并说明理由。
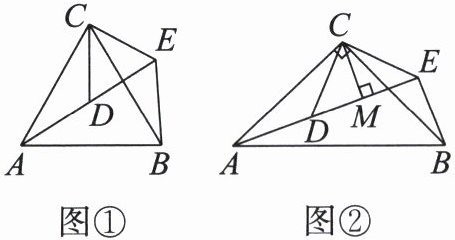
如图①,△ACB 和△DCE 均为等边三角形,点 A,D,E 在同一直线上,连接 BE。
①∠AEB 的度数为______;
②线段 AD,BE 之间的数量关系是______。
(2)拓展探究:
如图②,△ACB 和△DCE 均为等腰三角形,∠ACB= ∠DCE= 90°,点 A,D,E 在同一直线上,CM 为△DCE 中 DE 边上的高,连接 BE。请判断∠AEB 的度数及线段 CM,AE,BE 之间的数量关系,并说明理由。

答案:
解:
(1)①60° ②AD=BE
(2)∠AEB=90°,AE=2CM+BE.
理由如下:
因为△ACB和△DCE均为等腰三角形,∠ACB=∠DCE=90°,
所以AC=BC,CD=CE,∠BAC=∠ABC=∠CDE=∠DEC=45°,∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE,
所以△ACD≌△BCE,
所以AD=BE,∠BEC=∠ADC=135°,
所以∠AEB=∠BEC-∠CED=135°-45°=90°.
在等腰直角三角形DCE中,CM为斜边DE上的高,
所以∠DCM=∠ECM=45°,
所以∠DCM=∠ECM=∠CDE=∠DEC,
所以CM=DM=ME,所以DE=2CM,
所以AE=DE+AD=2CM+BE.
(1)①60° ②AD=BE
(2)∠AEB=90°,AE=2CM+BE.
理由如下:
因为△ACB和△DCE均为等腰三角形,∠ACB=∠DCE=90°,
所以AC=BC,CD=CE,∠BAC=∠ABC=∠CDE=∠DEC=45°,∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE,
所以△ACD≌△BCE,
所以AD=BE,∠BEC=∠ADC=135°,
所以∠AEB=∠BEC-∠CED=135°-45°=90°.
在等腰直角三角形DCE中,CM为斜边DE上的高,
所以∠DCM=∠ECM=45°,
所以∠DCM=∠ECM=∠CDE=∠DEC,
所以CM=DM=ME,所以DE=2CM,
所以AE=DE+AD=2CM+BE.
查看更多完整答案,请扫码查看


