《2025年人教金学典同步解析与测评八年级数学上册人教版云南专版》

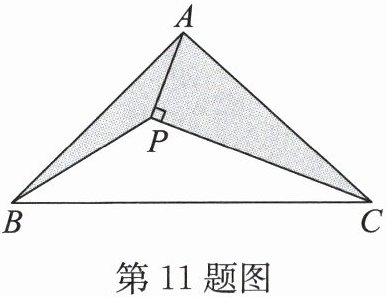
11. 如图,在 $ \triangle ABC $ 中,$ CP $ 平分 $ \angle ACB $,$ AP \perp CP $ 于点 $ P $,若 $ \triangle ABC $ 的面积为 $ 5 $,则阴影部分的面积为( )

A.$3.5$
B.$3$
C.$2.5$
D.$2$

答案： C

12. 如图,$ \angle MON = 90^{\circ} $,点 $ A $,$ B $ 分别在射线 $ OM $,$ ON $ 上移动,$ BC $ 平分 $ \angle OBA $,交 $ OM $ 于点 $ E $,$ AD $ 平分 $ \angle BAM $,$ AD $ 的反向延长线与 $ BC $ 交于点 $ C $。关于结论 $ I $,$ II $,下列判断正确的是( )
结论 $ I $：若 $ \angle BAD = 65^{\circ} $,则 $ \angle ABC = 40^{\circ} $。
结论 $ II $：无论点 $ A $,$ B $ 在射线 $ OM $,$ ON $(均不与点 $ O $ 重合)上怎样移动,$ \angle C $ 的度数都不变。

A.只有结论 $ I $ 正确
B.只有结论 $ II $ 正确
C.结论 $ I $,$ II $ 都正确
D.结论 $ I $,$ II $ 都不正确

答案： B

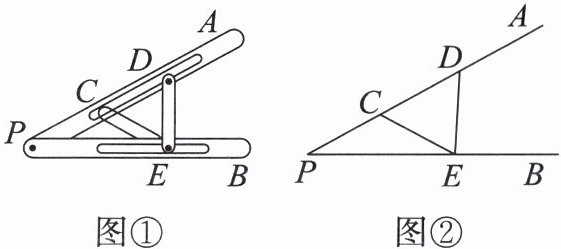
13. “三等分角”是古希腊三大几何问题之一,借助如图①所示的三等分角仪可以三等分角。这个三等分角仪的示意图如图②所示,有公共端点 $ P $ 的两条线段 $ PA $,$ PB $ 可以绕点 $ P $ 转动,点 $ C $ 固定,点 $ D $,$ E $ 在槽中可以滑动,且 $ CE = DE = CP $。若 $ \angle DEB = 87^{\circ} $,则 $ \angle P $ 的度数为( )

A.$29^{\circ}$
B.$14.5^{\circ}$
C.$17.4^{\circ}$
D.$30^{\circ}$

答案： A

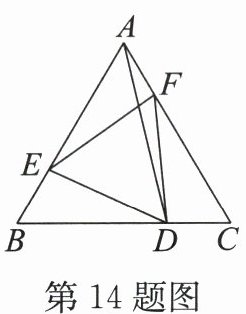
14. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ D $ 是 $ BC $ 上的一点,在 $ AB $,$ AC $ 上分别截取 $ BE = CD $,$ CF = BD $,连接 $ DE $,$ DF $,$ EF $,$ AD $。有下列结论：① $ \angle EDF = 90^{\circ} - \frac{1}{2} \angle BAC $；② $ \angle EDF = \angle B $；③ $ AD \perp BC $；④ $ \angle DEF = \angle DFE $。其中正确结论的序号是( )

A.①②
B.②④
C.①②③
D.①②④

答案： D

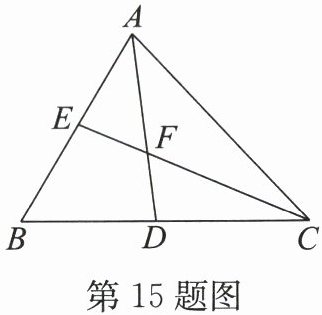
15. 如图,在 $ \triangle ABC $ 中,$ \angle ABC = 60^{\circ} $,$ AD $ 平分 $ \angle BAC $ 交 $ BC $ 于点 $ D $,$ CE $ 平分 $ \angle ACB $ 交 $ AB $ 于点 $ E $,$ AD $,$ CE $ 交于点 $ F $。有下列说法：① $ \angle AFC = 120^{\circ} $；② $ S_{\triangle ABD} = S_{\triangle ADC} $；③若 $ AB = 2AE $,则 $ CE \perp AB $；④ $ CD + AE = AC $；⑤ $ S_{\triangle AEF} : S_{\triangle FDC} = AF : FC $。其中说法正确的序号是( )


A.①②③
B.①③④
C.②③⑤
D.①③④⑤

答案： D

16. 如图,已知方格纸中有 9 个相同的小正方形,则 $ \angle 1 + \angle 2 $ 的度数为______ $^{\circ} $。

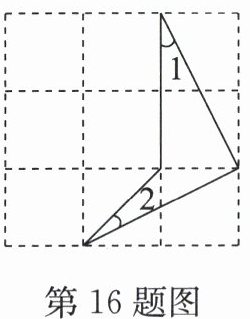
答案： 45

17. 如图,$ \triangle ABC \cong \triangle DEC $,点 $ B $,$ C $,$ D $ 在同一直线上,若 $ CE = 4 $,$ AC = 7 $,则 $ BD $ 的长为______。

答案： 11

18. 如图,在 $ \triangle ABC $ 中,$ BA = BC $,$ BD $ 平分 $ \angle ABC $,交 $ AC $ 于点 $ D $,点 $ M $,$ N $ 分别为 $ BD $,$ BC $ 上的动点,若 $ BC = 4 $,$ \triangle ABC $ 的面积为 $ 6 $,则 $ CM + MN $ 的最小值为______。

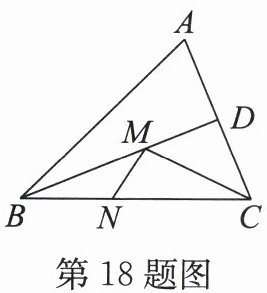
答案： 3