搜索
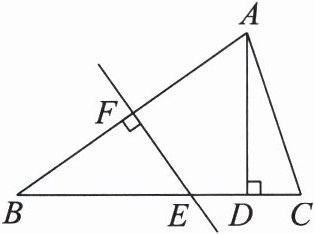
24. (8 分)如图,在 $ \triangle ABC $ 中,$ EF $ 是 $ AB $ 的垂直平分线,$ AD \perp BC $ 于点 $ D $,且 $ D $ 为 $ CE $ 的中点。
(1)求证：$ BE = AC $。
(2)若 $ \angle BEF = 55^{\circ} $,求 $ \angle BAC $ 的度数。
(1)求证：$ BE = AC $。
(2)若 $ \angle BEF = 55^{\circ} $,求 $ \angle BAC $ 的度数。
答案：
(1)证明:如图,连接AE.
(2)解:∠BAC=75°.
(1)证明:如图,连接AE.
(2)解:∠BAC=75°.
25. (8 分)如图,已知 $ \triangle ABC $ 的三个顶点的坐标分别是 $ A(-4,1) $,$ B(-3,3) $,$ C(-1,2) $。
(1)画出与 $ \triangle ABC $ 关于 $ y $ 轴对称的 $ \triangle A_1B_1C_1 $,并直接写出点 $ A_1 $,$ B_1 $,$ C_1 $ 的坐标；
(2)在 $ x $ 轴上有一点 $ D $,使得 $ \triangle ADC \cong \triangle ABC $,求点 $ D $ 的坐标。
(1)画出与 $ \triangle ABC $ 关于 $ y $ 轴对称的 $ \triangle A_1B_1C_1 $,并直接写出点 $ A_1 $,$ B_1 $,$ C_1 $ 的坐标；
(2)在 $ x $ 轴上有一点 $ D $,使得 $ \triangle ADC \cong \triangle ABC $,求点 $ D $ 的坐标。
答案：
(1)解:如图,△A₁B₁C₁即为所求.A₁(4,1),B₁(3,3),C₁(1,2).
(2)因为△ADC≌△ABC,所以AD=AB,CD=CB.因为点D在x轴上,所以点D的位置如图所示,所以点D的坐标为(-2,0).
(1)解:如图,△A₁B₁C₁即为所求.A₁(4,1),B₁(3,3),C₁(1,2).
(2)因为△ADC≌△ABC,所以AD=AB,CD=CB.因为点D在x轴上,所以点D的位置如图所示,所以点D的坐标为(-2,0).
26. (9 分)如图,在 $ Rt \triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,$ \angle BAC = 30^{\circ} $,分别以 $ AB $,$ AC $ 为边在 $ \triangle ABC $ 的外侧作等边三角形 $ ABE $ 和等边三角形 $ ACD $,连接 $ DE $,与 $ AB $ 交于点 $ F $,求证：$ EF = FD $。
答案：
证明:如图,过点E作EG⊥AB于点G.
因为△ABE是等边三角形,所以AG=$\frac{1}{2}$AB.因为在Rt△ABC中,∠BAC=30°,所以BC=$\frac{1}{2}$AB,所以AG=BC.又因为AE=AB,所以Rt△EAG≌Rt△ABC(HL),所以EG=AC=AD.因为△ACD是等边三角形,所以∠CAD=60°,所以∠DAB=90°,所以∠DAB=∠EGA.又因为∠EFG=∠DFA,所以△EFG≌△DFA(AAS),所以EF=FD.
证明:如图,过点E作EG⊥AB于点G.
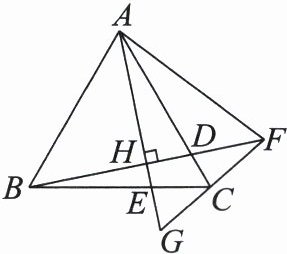
因为△ABE是等边三角形,所以AG=$\frac{1}{2}$AB.因为在Rt△ABC中,∠BAC=30°,所以BC=$\frac{1}{2}$AB,所以AG=BC.又因为AE=AB,所以Rt△EAG≌Rt△ABC(HL),所以EG=AC=AD.因为△ACD是等边三角形,所以∠CAD=60°,所以∠DAB=90°,所以∠DAB=∠EGA.又因为∠EFG=∠DFA,所以△EFG≌△DFA(AAS),所以EF=FD. 27. (12 分)如图,在等边三角形 $ ABC $ 中,$ D $ 为边 $ AC $ 上一点,连接 $ BD $ 并延长至点 $ F $,使得 $ AF = AC $,过点 $ A $ 作 $ AH \perp BF $ 于点 $ H $,$ AH $ 与 $ FC $ 的延长线交于点 $ G $。
(1)若 $ \angle CAF $ 的度数为 $ \alpha $,求 $ \angle AFC $ 的度数；(用含 $ \alpha $ 的代数式表示)
(2)求 $ \angle GFH $ 的度数；
(3)当 $ C $ 为 $ GF $ 的中点,且 $ CD = 1.5 $ 时,求 $ AD $ 的长。
(1)若 $ \angle CAF $ 的度数为 $ \alpha $,求 $ \angle AFC $ 的度数；(用含 $ \alpha $ 的代数式表示)
(2)求 $ \angle GFH $ 的度数；
(3)当 $ C $ 为 $ GF $ 的中点,且 $ CD = 1.5 $ 时,求 $ AD $ 的长。
答案：
解:
(1)因为AC=AF,所以∠ACF=∠AFC.又因为∠CAF=α,所以∠AFC=∠ACF=$\frac{1}{2}$(180°-∠CAF)=90°-$\frac{1}{2}$α.
(2)由题意可知∠BAC=60°,AB=BC=AC=AF,所以∠AFB=∠ABF=$\frac{1}{2}$(180°-∠BAF)=$\frac{1}{2}$(180°-∠BAC-∠CAF)=90°-$\frac{1}{2}$∠BAC-$\frac{1}{2}$∠CAF=60°-$\frac{1}{2}$∠CAF.因为∠AFC=∠ACF=$\frac{1}{2}$(180°-∠CAF)=90°-$\frac{1}{2}$∠CAF,所以∠GFH=∠AFC-∠AFB=90°-$\frac{1}{2}$∠CAF-(60°-$\frac{1}{2}$∠CAF)=30°.
(3)如图所示,连接BG,CH,过点C作CM⊥BF于点M,则∠CMF=90°.
由
(2),得∠GFH=30°,所以CM=$\frac{1}{2}$CF.因为AH⊥BF,所以∠FHG=90°,所以GH=$\frac{1}{2}$FG,∠FGH=60°.因为C为GF的中点,所以GH=CF=CG=$\frac{1}{2}$GF.因为∠FGH=60°,所以△CGH为等边三角形,所以CH=CG,∠GCH=∠ACB=60°,所以∠GCH-∠BCH=∠ACB-∠BCH,即∠GCB=∠HCA.因为△ABC是等边三角形,所以AC=BC.在△GCB和△HCA中,{BC=AC,∠GCB=∠HCA,GC=HC,所以△GCB≌△HCA(SAS),所以AH=BG.设GH=CG=CH=CF=a,则FG=2a,CM=$\frac{1}{2}$CF=$\frac{1}{2}$a.因为AB=AF,AH⊥BF,所以AG垂直平分BF,所以BG=GF=2a,所以AH=BG=2a.因为$S_{\triangle ADH}=\frac{1}{2}AH\cdot DH$,$S_{\triangle CDH}=\frac{1}{2}CM\cdot DH$,所以$\frac{S_{\triangle ADH}}{S_{\triangle CDH}}=\frac{AD}{CD}=\frac{\frac{1}{2}AH\cdot DH}{\frac{1}{2}CM\cdot DH}=\frac{2a}{\frac{1}{2}a}=4$.因为CD=1.5,所以AD=6.
解:
(1)因为AC=AF,所以∠ACF=∠AFC.又因为∠CAF=α,所以∠AFC=∠ACF=$\frac{1}{2}$(180°-∠CAF)=90°-$\frac{1}{2}$α.
(2)由题意可知∠BAC=60°,AB=BC=AC=AF,所以∠AFB=∠ABF=$\frac{1}{2}$(180°-∠BAF)=$\frac{1}{2}$(180°-∠BAC-∠CAF)=90°-$\frac{1}{2}$∠BAC-$\frac{1}{2}$∠CAF=60°-$\frac{1}{2}$∠CAF.因为∠AFC=∠ACF=$\frac{1}{2}$(180°-∠CAF)=90°-$\frac{1}{2}$∠CAF,所以∠GFH=∠AFC-∠AFB=90°-$\frac{1}{2}$∠CAF-(60°-$\frac{1}{2}$∠CAF)=30°.
(3)如图所示,连接BG,CH,过点C作CM⊥BF于点M,则∠CMF=90°.
由(2),得∠GFH=30°,所以CM=$\frac{1}{2}$CF.因为AH⊥BF,所以∠FHG=90°,所以GH=$\frac{1}{2}$FG,∠FGH=60°.因为C为GF的中点,所以GH=CF=CG=$\frac{1}{2}$GF.因为∠FGH=60°,所以△CGH为等边三角形,所以CH=CG,∠GCH=∠ACB=60°,所以∠GCH-∠BCH=∠ACB-∠BCH,即∠GCB=∠HCA.因为△ABC是等边三角形,所以AC=BC.在△GCB和△HCA中,{BC=AC,∠GCB=∠HCA,GC=HC,所以△GCB≌△HCA(SAS),所以AH=BG.设GH=CG=CH=CF=a,则FG=2a,CM=$\frac{1}{2}$CF=$\frac{1}{2}$a.因为AB=AF,AH⊥BF,所以AG垂直平分BF,所以BG=GF=2a,所以AH=BG=2a.因为$S_{\triangle ADH}=\frac{1}{2}AH\cdot DH$,$S_{\triangle CDH}=\frac{1}{2}CM\cdot DH$,所以$\frac{S_{\triangle ADH}}{S_{\triangle CDH}}=\frac{AD}{CD}=\frac{\frac{1}{2}AH\cdot DH}{\frac{1}{2}CM\cdot DH}=\frac{2a}{\frac{1}{2}a}=4$.因为CD=1.5,所以AD=6.
查看更多完整答案，请扫码查看
