21. (6 分)将一副直角三角尺按如图所示的方式摆放,等腰直角三角形 ABC 的斜边 BC 与含 30°角的直角三角形 DBE 的直角边 BD 长度相同,且斜边 BC 与 BE 在同一直线上,AC 与 BD 相交于点 O,连接 CD。求证:△CDO 是等腰三角形。


答案:
证明:因为在△BDC中,BC=BD,
所以∠BDC=∠BCD.
因为∠DBE=30°,
所以∠BDC=∠BCD=75°.
因为∠ACB=45°,
所以∠DOC=∠DBE+∠ACB=30°+45°=75°.
所以∠DOC=∠BDC,
所以△CDO是等腰三角形.
所以∠BDC=∠BCD.
因为∠DBE=30°,
所以∠BDC=∠BCD=75°.
因为∠ACB=45°,
所以∠DOC=∠DBE+∠ACB=30°+45°=75°.
所以∠DOC=∠BDC,
所以△CDO是等腰三角形.
22. (7 分)如图,在等边三角形 ABC 中,D 是 AC 的中点,E 是 BC 延长线上的一点,且 CE= CD,DM⊥BC,垂足为 M。求证:M 是 BE 的中点。
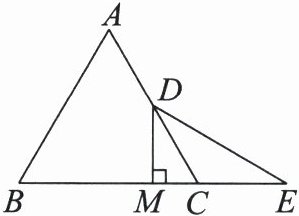

答案:
证明:如图,连接BD.

因为等边三角形ABC中,D是AC的中点,
所以∠DBC=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×60°=30°,∠ACB=60°.
因为CE=CD,
所以∠E=∠CDE.
又因为∠ACB=∠E+∠CDE,
所以∠E=$\frac{1}{2}$∠ACB=30°,
所以∠DBC=∠E=30°,
所以DB=DE.
又因为DM⊥BC,
所以M是BE的中点.
证明:如图,连接BD.

因为等边三角形ABC中,D是AC的中点,
所以∠DBC=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×60°=30°,∠ACB=60°.
因为CE=CD,
所以∠E=∠CDE.
又因为∠ACB=∠E+∠CDE,
所以∠E=$\frac{1}{2}$∠ACB=30°,
所以∠DBC=∠E=30°,
所以DB=DE.
又因为DM⊥BC,
所以M是BE的中点.
23. (7 分)如图,在四边形 ABCD 中,AD//BC,E 为 CD 的中点,连接 AE,BE,BE⊥AE,延长 AE 交 BC 的延长线于点 F。求证:
(1)CF= AD;
(2)AB= BC+AD。

(1)CF= AD;
(2)AB= BC+AD。

答案:
证明:
(1)因为AD//BC,
所以∠ADE=∠FCE.
因为E是CD的中点,
所以DE=CE.
在△ADE与△FCE中,
{∠ADE=∠FCE,
DE=CE,
∠AED=∠FEC,
所以△ADE≌△FCE(ASA),
所以CF=AD.
(2)因为△ADE≌△FCE,
所以AE=EF.
又因为BE⊥AE,
所以BE是线段AF的垂直平分线,
所以AB=BF=BC+CF.
因为CF=AD,
所以AB=BC+AD.
(1)因为AD//BC,
所以∠ADE=∠FCE.
因为E是CD的中点,
所以DE=CE.
在△ADE与△FCE中,
{∠ADE=∠FCE,
DE=CE,
∠AED=∠FEC,
所以△ADE≌△FCE(ASA),
所以CF=AD.
(2)因为△ADE≌△FCE,
所以AE=EF.
又因为BE⊥AE,
所以BE是线段AF的垂直平分线,
所以AB=BF=BC+CF.
因为CF=AD,
所以AB=BC+AD.
24. (8 分)如图,在四边形 ABCD 中,AD= BC,∠A= ∠B,E 为 AB 的中点,连接 CE,DE。
(1)求证:△ADE≌△BCE。
(2)若∠A= 70°,∠BCE= 60°,求∠CDE 的度数。
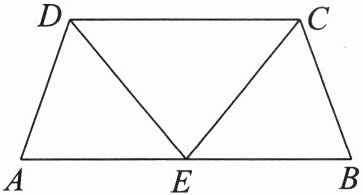
(1)求证:△ADE≌△BCE。
(2)若∠A= 70°,∠BCE= 60°,求∠CDE 的度数。

答案:
(1)证明:因为E为AB的中点,
所以AE=BE.
又因为AD=BC,∠A=∠B,
所以△ADE≌△BCE.
(2)解:由
(1)得△ADE≌△BCE,
所以DE=EC,∠ADE=∠BCE=60°,∠AED=∠BEC.
因为∠A=∠B=70°,
所以∠AED=∠BEC=180°-60°-70°=50°,
所以∠DEC=180°-50°-50°=80°.
因为DE=EC,
所以∠CDE=$\frac{1}{2}$×(180°-80°)=50°.
(1)证明:因为E为AB的中点,
所以AE=BE.
又因为AD=BC,∠A=∠B,
所以△ADE≌△BCE.
(2)解:由
(1)得△ADE≌△BCE,
所以DE=EC,∠ADE=∠BCE=60°,∠AED=∠BEC.
因为∠A=∠B=70°,
所以∠AED=∠BEC=180°-60°-70°=50°,
所以∠DEC=180°-50°-50°=80°.
因为DE=EC,
所以∠CDE=$\frac{1}{2}$×(180°-80°)=50°.
查看更多完整答案,请扫码查看


